👩🏼‍🔬 🙌🏿 🔕 希格斯场如何工作：3）希格斯粒子如何出现 👨🏾‍✈️ 👩‍🎓 🧝🏾

希格斯场如何工作：

在上一篇文章中，我描述了希格斯字段的平均值为何不为零以及为什么不为零。现在，我要描述希格斯粒子是什么以及它的质量如何从方程式产生。

我想提醒您，如果未提及相反的内容，我将始终描述该场和希格斯粒子的最简单形式-所谓的希格斯标准模型。更复杂的形式也是可能的。例如，多个希格斯字段可能同时存在，而不是一个。也许我将在以下文章之一中描述一个更复杂的情况。

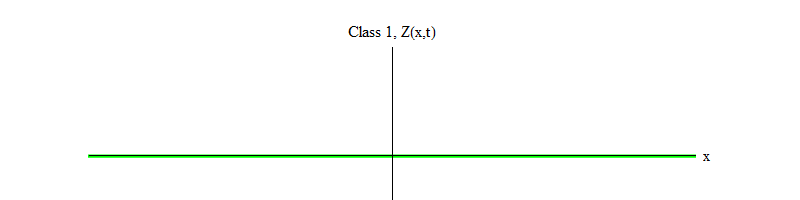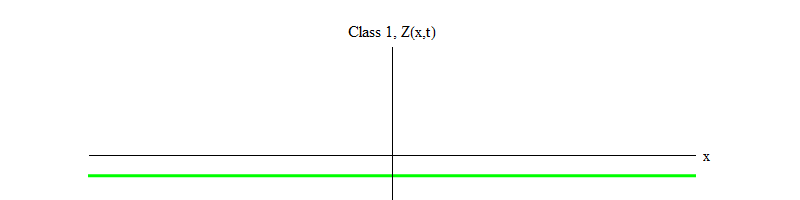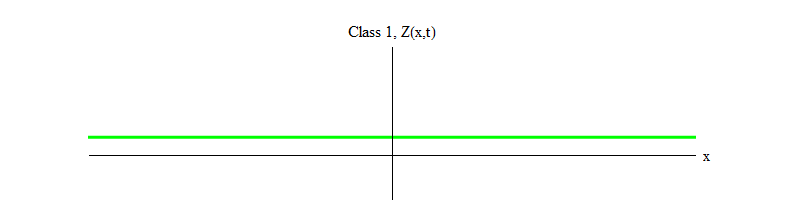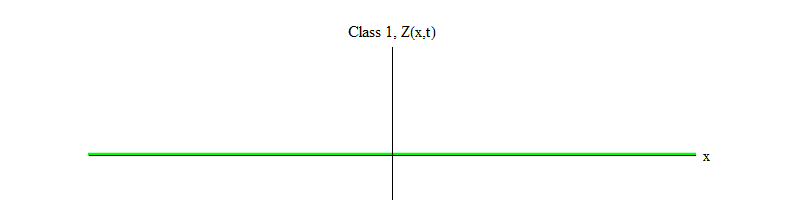图 1：1类场随时间稳定在Z（x，t）= 0的附近波动

在上一篇文章中，我没有强调这个事实，但是在我们自然界中发现的基本领域中，希格斯领域是独一无二的。除了希格斯场外，所有场都满足0或1类的运动方程。实际上（尽管自然界中的所有场可能并非如此），但我们知道满足希格斯场为1的方程的所有场都这样做，因为希格斯场为非零。如果为零，它们都将满足0级方程（如我在第一篇文章中所述）。而是，希格斯场满足可以称为-1级方程的方程。

对于字段Z（x，t），我定义的类如下所示：

d^{2} Z / d t^{2} - c^{2} d^{2} Z / d x^{2} = - B^{2} Z q u a d [类 别 1 - 大 量 粒 子] d^{2} Z / d t^{2} - c^{2} d^{2} Z / d x^{2} = 0 q u a d [0 类 - 无 质 量 粒 子] d^{2} Z / d t^{2} - c^{2} d^{2} Z / d x^{2} = + B^{2} Z q u a d [类 别 - 1 - 不 稳 定]

$d ^ 2Z / dt ^ 2-c ^ 2 d ^ 2Z / dx ^ 2 =-B ^ 2 Z \ quad [类别1-大量\;粒子] \\ d ^ 2Z / dt ^ 2-c ^ 2 d ^ 2Z / dx ^ 2 = 0 \ quad [0类-无质量\;粒子] \\ d ^ 2Z / dt ^ 2-c ^ 2 d ^ 2Z / dx ^ 2 = + B ^ 2 Z \ quad [类别-1-不稳定]$

该等式表明B ² > 0。

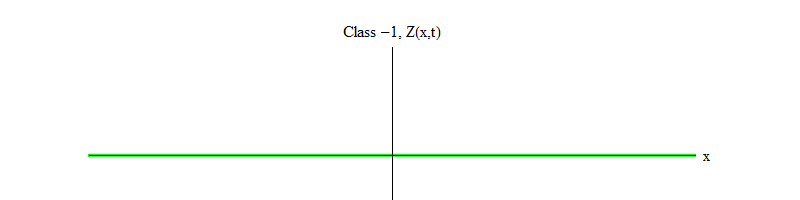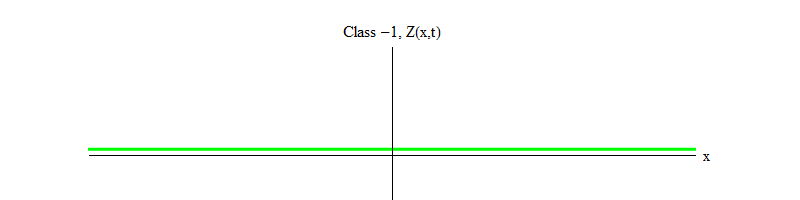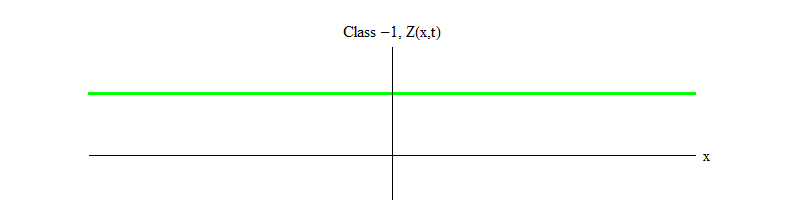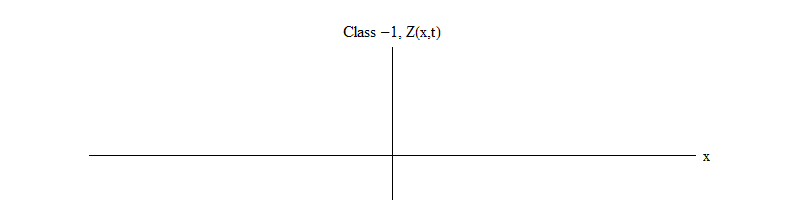图 2：类别-1的场离开不稳定的平衡点Z（x，t）= 0。

1类和-1类之间的减号非常重要。在这两种情况下，方程的解都包含Z（x，t）= 0作为特殊情况之一，但是对于1类，Z（x，t）= 0是稳定的，也就是说Z（x，t）可以在零附近波动；这些正以巨大的量子行为。反之亦然，类别-1 Z（x，t）= 0是不稳定的，也就是说Z（x，t）不会波动，但是会增长到越来越多的值。如果不更改方程式，则场的大小会飞到无穷大。更准确地说，如果对类1的方程的解是振动Z，则如图2所示。如图1所示，类别-1方程的解是Z的指数增长。 2。

对于希格斯场以及自然界中存在的任何场，使用限制指数增长并防止该场变为无穷大的项来更改-1类方程。正如我们在上一篇文章中看到的，希格斯场服从运动方程

d^{2} H / d t^{2} - c^{2} d^{2} H / d x^{2} = - b^{2} H （ H^{2} - v^{2} ） = + （ b v ）^{2} H - b^{2} H^{3}

$d ^ 2H / dt ^ 2-c ^ 2 d ^ 2H / dx ^ 2 =-b ^ 2 H（H ^ 2-v ^ 2）= +（bv）^ 2 H-b ^ 2 H ^ 3$

当H几乎为零时，它属于-1类，但是它具有H ³的重要成员。这里b是一个正数，v是H的平衡位置。该方程式确保，如果磁场H在点H = 0处开始并且从不稳定平衡的位置移动到正H，那么它将在H = v的稳定平衡的位置附近振荡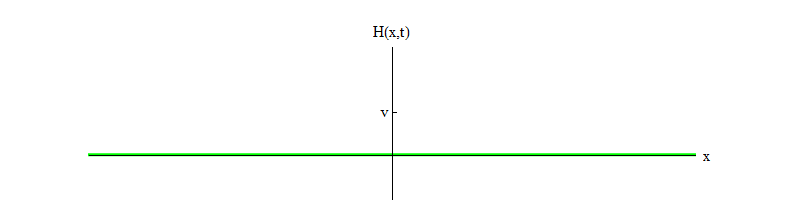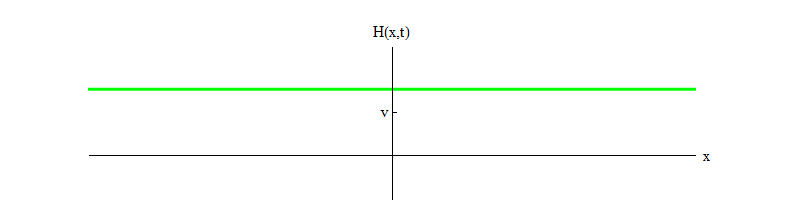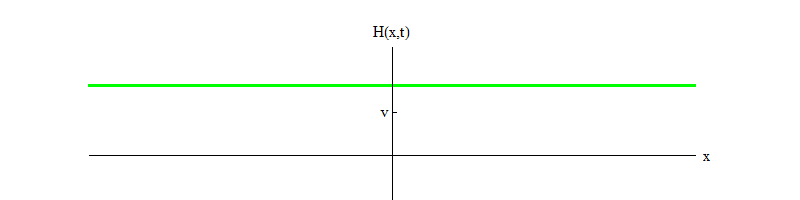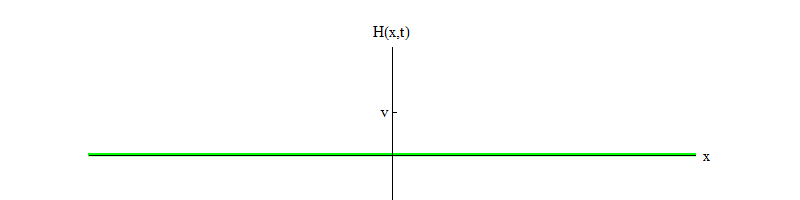（图3）。

图 3

随着时间的流逝，由于运动方程的项，振荡将逐渐消失，为简便起见，我将其省略；它们使场H的部分振荡能量转移到其他场的波中（这些非线性项使希格斯粒子衰减）。随着时间的流逝（图4），磁场H将在位置H = v处平静下来。

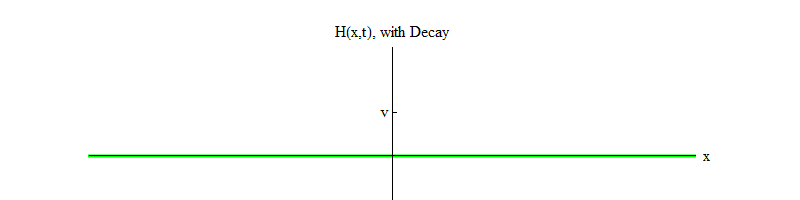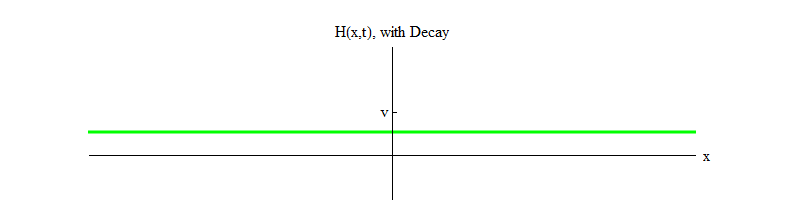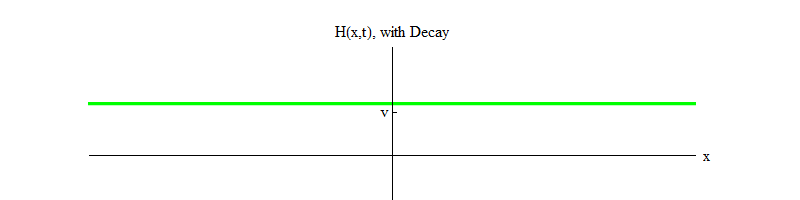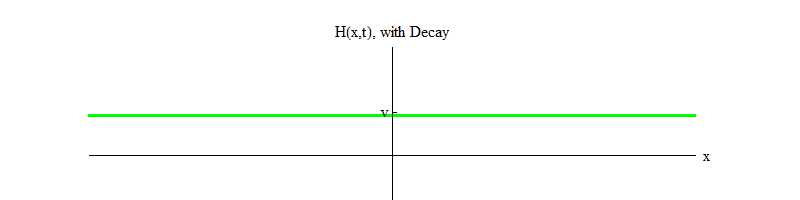图 4

如果有任何物理过程在很小的空间区域内将位置H = v击中场，则该场将发出以下形式的波：

H = v + A c o s [2 p i （ n u t - x / l a m b d a ）]

$H = v + A cos [2 \ pi（\ nu t-x / \ lambda）]$

其中A是波幅，ν和λ是频率和波长，并且ν和λ之间的关系取决于运动方程的确切形式，尤其是b和v。这些波的量子将是希格斯粒子。每百万个问题：希格斯粒子的质量是多少？为了计算这一点，我们需要像粒子（代表相对论场中的波量子）一样始终需要确定频率ν和相应场的波的波长λ之间的关系，然后将结果乘以普朗克常数h来获得能量之间的比率这些波的量子动量，这将告诉我们量子（即粒子）的质量。

我们只用第一篇文章中提到的字段S（x，t）来做到这一点。我们编写希格斯场的平移版本，将其表示为H（x，t）= v + h（x，t） ，并将其代入场H的运动方程。h （x，t）我将用粗体字区分它根据普朗克常数h。在评论文章中给出的场S的示例中，显示了一个简单的运动方程，因此，移动并未改变粒子S的质量。但是在这种情况下，它没有改变！希格斯场运动方程更为复杂，因此h的方程与H的原始方程有很大不同：

d^{2} t e x t b f h / d t^{2} - c^{2} d^{2} t e x t b f h / d x^{2} = - b^{2} （ v + t e x t b f h ） （ 2 v t e x t b f h + t e x t b f h^{2} ）

$d ^ 2 \ textbf {h} / dt ^ 2-c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 =-b ^ 2（v + \ textbf {h}）（2 v \ textbf {h} + \ textbf {h} ^ 2）$

我在这里使用v是一个常数并且独立于空间和时间的事实。然后我们回想起希格斯场量子的幅度很小，因此，当研究唯一的希格斯粒子时（正是我们需要确定其质量），我们可以舍弃所有与h ²和h ³成比例的项：

d^{2} t e x t b f h / d t^{2} - c^{2} d^{2} t e x t b f h / d x^{2} = - 2 b^{2} v^{2} t e x t b f h + . . .

$d ^ 2 \ textbf {h} / dt ^ 2-c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 =-2 b ^ 2 v ^ 2 \ textbf {h} + ...$

“ + ...”表示撤回的成员。注意，尽管我们从H（x，t）的-1类方程开始，但h（x，t）的该方程属于1类。这是因为H（x，t）在H = 0的区域中不稳定，而h （x，t）在h = 0的区域，其中H = v是稳定的。因此，我们可以使用以下类别的等式的形式来计算希格斯粒子h的质量m _h ：

m_{h} = s q r t 2 （ h / 2 p i ） b v / c^{2}

$m_h = \ sqrt2（h / 2 \ pi）b v / c ^ 2$

右侧的h表示普朗克常数。如果最近在大型强子对撞机上发现的类似希格斯粒子真的是标准模型的希格斯粒子，那么我们第一次可以找出b是什么（记住v我们早就知道了），最后我们可以找到a = b的值v。

v = 246 GeV；
m h≈125 GeV /c²（如果新粒子是希格斯）
b≈0.35（2π/ h）（如果新粒子是标准模型的希格斯）
a = bv≈87 GeV（2π/ h）（如果新粒子是标准模型的希格斯）

h也是普朗克常数。直到最近发现希格斯粒子后，我们才知道最后三个数量。

现在，如果事实证明标准模型不符合自然（如果除了H（x，t），还需要在已知字段中添加其他字段以解释最近发现的质量为125 GeV /c²的粒子的性质），那么我们假设该粒子是几个粒子之一希格斯粒子的类型-那么我们将不得不在大型强子对撞机上处理这种困难的情况再持续几年。您可以想象很多可能性，没有必要向所有人解释它们，但是在这里我大致描述了其中一些。如果在大型强子对撞机上收到的数据能向我们显示一定的方向，我将向您详细解释所有内容。

希格斯场如何工作：3）希格斯粒子如何出现

More articles: