古典力学很直观：人们每天反复使用它来维持生存。 但是直到二十世纪，还没有人使用过量子力学。 她描述的东西是如此之小，以至于它们完全不属于人类的感知。 理解这一理论，享受其美丽的唯一途径是用抽象数学来阻碍我们的直觉。
美国著名科学家伦纳德·萨斯金（Leonard Sasskind）邀请您前往量子力学这个国家，进行一次激动人心的旅程。 途中，您将需要学校物理课程的基础知识，以及数学分析和线性代数的基础知识。 您还需要了解Susskind的第一本书“理论最低限度”中所涉及的问题-“您需要了解的有关现代物理学的一切。” 但是，如果某种程度的知识被遗忘，这是无所畏惧的。 许多作者将在此过程中提醒和解释。
量子力学是一个不寻常的理论：例如，根据其假设，我们可以了解有关系统的所有知识，而不能了解其各个部分。 爱因斯坦和尼尔斯·玻尔对此和其他矛盾进行了很多争论。 如果您不惧怕困难，有好奇心，对技术有能力，对物理学有真诚和浓厚的兴趣，那么伦纳德·萨斯金德（Leonard Sasskind）的这门讲座将吸引您。 该书侧重于量子理论的逻辑原理，其目的不是消除量子逻辑的悖论，而是将其拉入现实，并试图解决它提出的难题。
波形功能概述
在本讲座中，我们将使用波动函数的语言，因此让我们在潜水之前简要回顾一下材料。 我们在第5讲中讨论了抽象对象的波动函数，但没有解释它们与波动或函数之间的关系。 在填补这一空白之前，我提醒您我们先前讨论的内容。
首先，我们选择特征值为l且特征向量为| l〉的可观察L。 令| Y〉为状态向量。 由于Hermitian算子的特征向量形成完整的正交基，因此向量| Y〉可以在此基础上扩展：
如您在5.1.2和5.1.3节所述，量Y（l）被称为系统的波动函数。 但请注意：Y（l）的特定形式取决于我们最初选择的特定可观察的L。 如果我们选择另一个可观察值，尽管我们仍在谈论同一状态，但波动函数（以及基向量和特征值）将变得不同。 因此，我们必须保留Y（l）是与|Yñ相关的波动函数。 确切地说，我们必须说Y（l）是L基中的波动函数。 如果我们使用向量<li | lj> = dij的正交性性质，那么也可以使用特征向量| l〉的状态向量| Y〉的内积（或投影）来定义L基中的波动函数：Y（l ）= 〈L | Y〉
有两种考虑波动函数的方法。 首先，这是特定状态下状态向量的一组集合。 这些组件可以以列向量的形式编写：
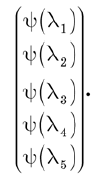
考虑波动函数的另一种方法是将其视为l的函数。 如果设置l的任何有效值，则函数Y（l）会给出一个复数。 因此，可以说Y（l）是离散变量l的复数值函数。 考虑到这一点，线性运算符成为适用于函数并提供新函数的运算。
最后提醒一下：实验给出结果l的概率等于P（l）= Y *（l）Y（l）。
函数和向量
到目前为止，我们研究的系统都具有有限维状态向量。 例如，简单的自旋由二维状态空间描述。 因此，可观察值只有有限数量的可能的可观察值。 但是，还有更复杂的可观测值，它们可以具有无限数量的值。 一个例子是粒子。 粒子坐标是可以观察到的，但与自旋不同，坐标具有无限数量的可能值。 例如，沿x轴移动的粒子可以位于任何材质标记x处。 换句话说，x是一个连续的无限变量。 当观察到的系统是连续的时，波动函数成为连续变量的成熟函数。 为了将量子力学应用于这类系统，我们必须扩展矢量的概念，以便在其中包含功能。
函数是函数，向量是向量； 它们似乎是完全不同的实体，那么函数向量在什么意义上呢？ 如果将向量视为三维空间中的箭头，那么它们当然与函数完全不同。 但是，如果您更广泛地看矢量，就像满足某些假设的数学对象一样，这些函数实际上会形成一个矢量空间。 为了纪念数学家戴维·希尔伯特（David Hilbert），通常将这种矢量空间称为希尔伯特空间。
考虑一个实变量x的复数函数Y（x）的集合。 复数函数是指每个x将复数Y（x）关联。 另一方面，自变量x是普通的实变量。 它可以取从–∞到+∞的任何实数值。
现在，我们通过说“功能是向量”来确切地表达我们的意思。 这不是表面的类比或隐喻。 在某些限制下（我们稍后将返回），诸如Y（x）的函数满足定义矢量空间的数学公理。 我们在1.9.2节中简要提到了这个想法，现在我们全力使用它。 回顾复矢量空间的公理（在1.9.1节），我们看到复函数满足了它们的全部。
1.任何两个函数的和是一个函数。
2.功能的增加是可交换的。
3.功能的增加是关联的。
4.有一个唯一的零功能，这样，当将其添加到任何功能时，便会获得相同的功能。
5.对于任何给定的函数Y（x），都有一个唯一函数–Y（x），使得Y（x）+（–Y（x））= 0。
6.函数乘以任何复数即可得到一个函数，并且是线性的。
7.观察到分布特性，这意味着
z [Y（x）+ j（x）] = zY（x）+ zj（x），
[z + w] Y（x）= zY（x）+ wY（x），
其中z和w是复数。
所有这些都意味着我们可以在抽象向量空间中用ket向量| Y〉来识别函数Y（x）。 我们也可以定义胸罩矢量也就不足为奇了。 用复共轭函数Y *（x）识别对应于chum sal | Y>的文胸向量<Y |。
为了有效地使用这一思想，我们需要从数学工具集中概括一些对象。 在以前的讲座中，标识波动函数的标签是某些有限离散集的成员，例如，某个可观测值的特征值。 但是现在自变量是连续的。 除其他外，这意味着我们不能使用普通金额对其进行汇总。 我想你知道该怎么办。 这是我们三个向量概念的面向功能的替代品，您已经熟悉其中的两个。
•金额被积分代替。
•用概率密度代替概率。
•Kronecker增量符号由Dirac增量功能代替。
让我们仔细看看这些工具。
金额由积分代替 。 如果我们确实想保持严谨性，我们首先将x轴替换为以非常小的间隔ε隔开的离散点集，然后继续执行极限ε→0。这将需要几页来证明每个步骤的合理性。 但是我们可以通过一些直观的定义来避免这种麻烦，例如用积分替换和。 从原理上讲，此方法可以编写如下：
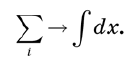
例如，如果您需要计算曲线下的面积，则将x轴划分为小段，然后将大量矩形的面积相加，就像在基本数学分析中一样。 当我们让线段收缩到零大小时，总和成为整数。
考虑括号<Y | 和ket | Y〉并定义其内积。 这样做的明显方法是用积分代替公式（1.2）中的求和。 我们将内积定义如下：
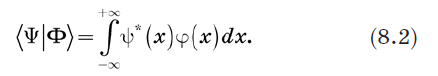概率由概率密度代替 。 接下来，我们用变量x的概率密度来标识P（x）= Y *（x）Y（x）。 为什么具有概率密度，而不仅仅是概率？ 如果x是一个连续变量，则它将采用任何确切给定值的概率通常为零。 因此，这样提出问题更正确：x位于两个值x = a和x = b之间的概率是多少？ 确定概率密度，以使该概率由积分给出
由于总概率必须为1，我们可以将向量的归一化定义为
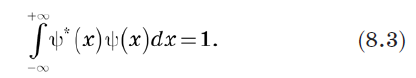Kronecker delta符号由Dirac delta函数代替 。 到目前为止，一切都非常熟悉。 Dirac Delta功能是新功能。 增量函数是Kronecker增量符号dij的类似物，根据定义，如果i≠j，则为0；如果i = j，则为1。 但是可以用另一种方式定义。 考虑有限维空间中的任何向量Fi。 不难看出，克罗内克三角洲符号满足条件
这是由于这样一个事实，即只有j = i的项在此和中不为零。 在求和期间，Kronecker符号会滤除F之外的F的所有成分。 一个明显的概括是定义一个新函数，该函数在积分下使用时具有相同的过滤属性。 换句话说，我们需要一个新的实体d（x-x'），该实体的属性对于任何函数F（x）
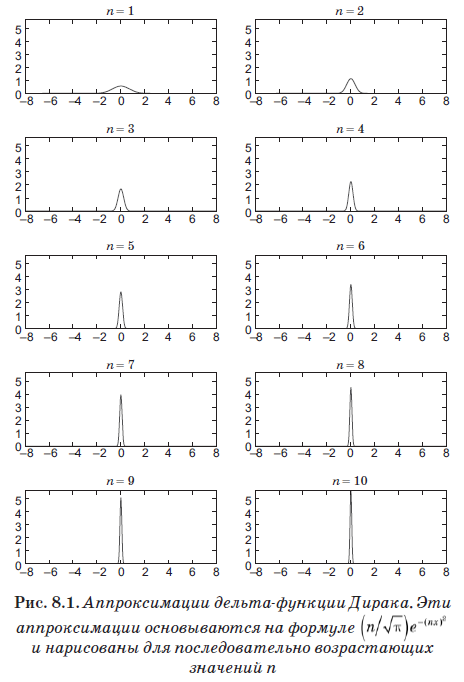
等式（8.4）定义了一个称为狄拉克δ函数的新实体，该实体被证明是量子力学中最重要的工具。 但是，尽管它有名字，但这并不是通常意义上的功能。 当x≠x'时，它等于零，但是当x = x'时，它变为无穷大。 实际上，它恰好是无限的，因此d（x）下的面积等于1。大致来说，该函数在无限小的间隔ε上为非零，但在该间隔上的值为1 /ε。 因此，它下面的面积等于1，更重要的是，它满足方程式（8.4）。 功能介绍
对于非常大的n值，delta函数非常近似。 在图。 8.1显示了n的递增值的优化。 尽管我们将n = 10（即非常小的值）定为一个事实，但请注意，该图形已经变成非常狭窄且尖锐的峰值。
»这本书的更多信息可以
在出版商的网站上找到»
目录»
摘录对于此博客的读者，优惠券可享受20％的折扣
-Sasskind