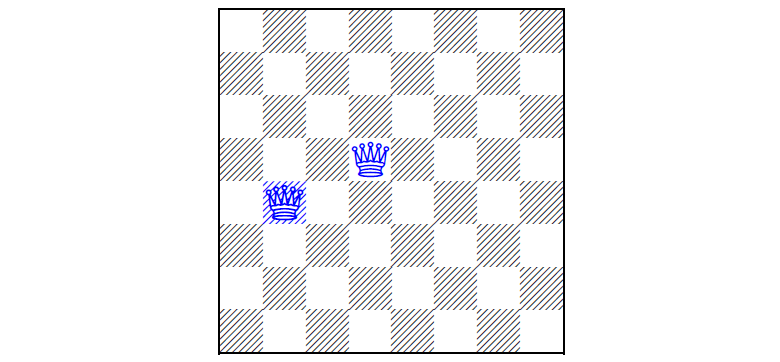
拼图的第一个版本于1850年，当棋盘上预先安装了两个皇后，并且玩家必须安排其余的皇后（有关此问题的两种解决方案，请参见下图）N个皇后的问题是将N个皇后放置在N×N板上，这样就不会有另一个皇后受到另一个皇后的战斗，而板上要预先安装几个皇后。 也就是说，最后，没有两个皇后应该在同一条直线或对角线上。 这个问题最早是在1848年提出的，并在1850年提出了一个拼图变体，事先将一定数量的女王/王后放在棋盘上，如果可能的话，玩家应该安排其余的。
苏格兰圣安德鲁斯大学的研究人员发表了
一篇科学文章，证明N-皇后问题不仅是＃P-完全的，而且是NP-完全的。 此外，克莱数学研究所（美国）准备向任何能够优化该问题作为证明问题P = NP的人支付一百万美元。
如您所知，在复杂性理论中，＃P是一类问题，其解决方案是成功的数量，即在多项式时间内运行的某些不确定性图灵机的成功进入接纳状态的计算路径。 #P类的计算问题（计数问题）与NP类的相应决策问题有关。
科学家注意到，这项任务可能是NP完全任务中最简单的任务，它可以向任何了解国际象棋游戏规则的人解释这些问题的实质。 这个任务有一个非常有趣的故事。 一次，她引起了高斯的注意，高斯甚至在她的决定中犯了一个小错误（在8×8的董事会上，他报告了76个决定，但随后他意识到其中四个是错误的，因此只剩下72个决定，后来高斯确立了所有92个决定。对于8×8的板子）。
N×N电路板问题的概括引起了许多数学家的注意。 在过去的半个世纪中，已经发表了数十篇致力于该问题的科学论文。 至少有6个在Google学术搜索中被引用了400次以上：这是Golomb＆Baumert，1965； Bitner＆Reingold，1975年； Mackworth＆Freuder，1985年； Minton，Johnston，Philips和Laird，1992； Selman，Levesque＆Mitchell，1992； 克劳福德，金斯伯格，卢克斯和罗伊，1996年。
N-Queens问题的复杂性常常被误判。 即使在大量引用的作品中，也经常将其称为NP难题（NP-hard问题），但只有在P = NP的情况下才会如此。 实际上，该问题的计算形式（即确定N个皇后的
解数）是“整数序列在线百科”中的
序列A000170 。 现在已知n = 27时该序列最大，其中解的数量超过2.34×10
17 。 没有比简单的穷举搜索更有效的解决方案。 因此，对于2016年的n = 27，使用了FPGA上的大规模并行搜索。
同时，如果计算机开始枚举皇后号在1000×1000单元板上的可能位置，则它将永远加载此任务。 根据科学家的说法，如果有人找到一种非常快速有效的解决方法，他们将可以从克莱数学研究所获得超过一百万美元的收益。 “如果您编写的程序能够真正快速地解决问题，则可以使它适应解决我们每天面临的许多重要任务，”科学工作的作者之一计算机科学教授Ian Gent说。 “其中有一些琐碎的问题，例如在Facebook上找到最大的一群彼此不认识的朋友，或者非常重要的任务，例如确保我们所有在线交易安全的黑客代码。”
但是这些纯粹是理论上的捏造。 实际上，还没有人以快速有效的方式来解决N个皇后问题。 为了证明有比简单地枚举所有选项更有效的方法来解决问题，他们将提供一百万美元。
2017年8月在《
人工智能研究杂志
》上 发表了一篇科学文章（doi：10.1613 / jair.5512，
pdf ）。
PS解决KDPV问题的两种方法：
