
“理论最低限度”是一本书,适合那些在学校和研究所错过物理课但已经后悔的人。 是否想了解自然科学的基础并像现代物理学家一样学习如何思考和推理? 以原始和非标准的形式,美国著名科学家伦纳德·萨斯金德(Leonard Sasskind)和乔治·格拉博夫斯基(George Grabowski)为好奇的人们提供了数学和物理学入门课程。
与其他通俗的科学书籍试图以通俗易懂的方式解释物理学定律,巧妙地避免使用方程式和公式的方法不同,作者教给读者自然科学的经典基础。 本书提供了自己的原创教学方法,并在
理论上以videominimum.com发行的视频讲座作为补充。
讲座9.相流体与吉布斯-利维尔定理
兰尼喜欢看河,特别是看着浮在水面上的小斑点。 他试图想象它们将如何在石头之间移动或掉入漩涡中。 但是整个河道-大量水的汇合,溪流相互分离,汇聚和相互超越-超出了他的理解。
相流体对于经典力学来说,专注于特定的初始条件并在相空间中遵循单独的轨迹是很自然的。 但是,还有一个更广阔的视野,涵盖了整个轨迹系列。 与其将铅笔的笔尖放在相空间中的某个点并从那里追踪唯一的路径,我们将尝试做一些更雄心勃勃的事情。 想象一下,我们有无限数量的铅笔,并使用它们,以便我们用点均匀地填充相空间(通过均匀性,我的意思是q,p中点的密度在任何地方都是相同的)。 将这些点视为构成填充相空间的虚构流体的粒子。
现在让每个点根据哈密顿运动方程式运动:
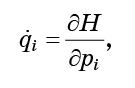
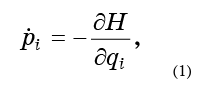
这样我们的流体就会无休止地流过相空间。
谐波振荡器是一个很好的初始示例。 在第8课中,我们看到每个点都以恒定的角速度沿圆形轨道运动。 (让我提醒您,我们谈论的是相位,而不是坐标空间。在坐标中,振荡器在一个维度上来回移动。)整个流体整体上呈固体运动,围绕相空间的原点均匀旋转。
现在回到一般情况。 如果坐标数为N,则相空间和其中的液体为2N维。 流体以一种非常特定的方式流动。 它的流动具有特殊的性质。 其中之一是,如果一个点以某个能量开始-即对于给定的H(q,p)值-那么它将存储该能量值。 恒定能量(例如能量等于E)的表面由方程H(q,p)= E决定。(2)
对于E的每个值,我们有一个方程,该方程具有2N个相空间变量,这些变量定义了尺寸为2N-1的表面。 当您遍历所有E值时,这些曲面将填充整个相空间。 我们可以将等式(2)给出的表面的相空间视为等高线图(图1),其上的水平线不代表高度,而是能量值。 如果液体点在特定的表面上,它将永远保留在其上。 这就是能量守恒定律。
谐波振荡器的相空间是二维的,能量面是圆形的:
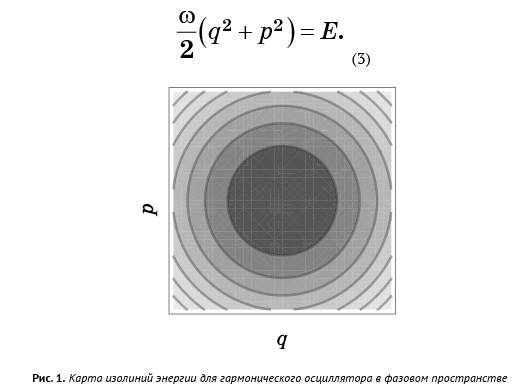
在一般情况下,机械系统的能量表面太复杂而无法可视化,但原理仍然是相同的:
能量表面会随着层的增加而填充相空间,并且流动会移动,从而使这些点保留在它们最初所在的表面上 。
简短提醒我想在这里停下来,回想一下在第一堂课中所说的话,当时讨论了硬币,骰子和关于运动定律的最简单的想法。 我们用一组箭头将这些定律描述出来,这些箭头连接了代表系统状态的点。 我们还解释了法律是可以接受的和不可接受的,而可以接受的是可逆的。 最重要的是,每个点都必须恰好有一个入方向箭头和正一个出方向箭头。 如果至少在某一点上箭头的数量超过了箭头的数量(这称为收敛),则这种定律是不可逆的。 当外向箭头的数量大于外向箭头的数量时(称为发散),情况也是如此。 箭头的发散和会聚都违反了可逆性,因此被禁止。 到目前为止,我们还没有回到这一推理领域。 现在是时候了。
流动与分歧考虑普通空间中流体流动的一些简单示例。 有一会儿,我们忘记了相空间,只考虑了在通常的三维空间中移动的普通流体,其轴分别表示为x,y,z。 流动可以用
速度场来描述。 速度场
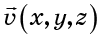
通过在空间的每个点上设置速度矢量来确定(图2)。
您还可以使用速度分量来描述速度场:
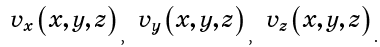
同样,某一点的速度可能取决于时间,但我们假设不存在这种依赖关系。 在这种情况下,该流称为
平稳流。
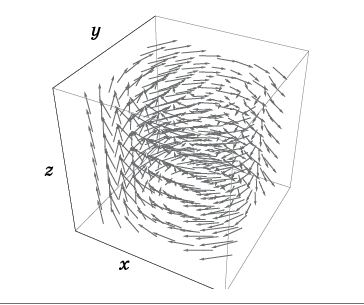
图 2.速度场
花费相同的数量。 这也意味着流体的密度(每单位体积的分子数)在任何地方都是相同的,并且随着时间的推移是恒定的。 顺便说一下,术语“不可压缩性”也表示不可扩展性。 换句话说,液体不能增加体积。 考虑一个由条件定义的小立方单元:
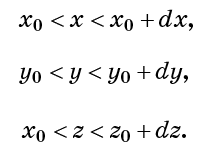
不可压缩性意味着每个这样的单元中的流体点数是恒定的。 这也意味着进入单元的总流体流量(每单位时间)必须为零。 (进入多少个流点,存在相同数目的流出口。)考虑每单位时间通过细胞表面的分子数x = x0。 它与该表面上的流速vx(x0)成正比。
如果速度vx在x0和x0 + dx处相同,则通过x = x0进入单元的流量将与通过x = x0 + dx进入单元的流量相同。 但是,如果vx在整个单元中发生变化,则这两个流将不平衡。 通过这两个面进入单元的总流量将成比例
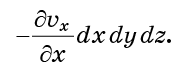
面y0和y0 + dy以及z0和z0 + dz完全相同。 如果全部添加,则分子进入细胞的总流量(流入量减去流出量)
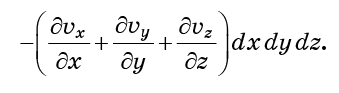
括号中的导数组合称为矢量场的散度
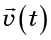
并被指定
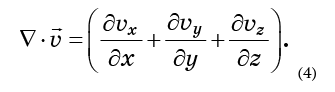
散度反映了分子的分散程度或分子占据的体积的增加。 如果流体不可压缩,则该体积不应改变,这意味着散度应为零。
理解不可压缩性的一种方法是想象每个分子或每个点都占据了无法改变的体积。 它们不能被压缩到较小的体积,它们不会消失,也不会无处不在。 稍加思考,您就会看到不可压缩和可逆的相似之处。 在第1课中分析的示例中,箭头还确定了一种流程。 基本上,该流是不可压缩的,至少是可逆的。 由此产生的自然问题是:相空间中的流动是否可逆? 如果系统满足汉密尔顿方程,答案是肯定的。 表示这种不可压缩性的定理称为Liouville定理。
里维尔定理让我们回到相空间中的流体流动,并考虑相空间中每个点的流体速度分量。 不必说相流体在坐标x,y,z中不是三维的。 在坐标pi,qi中为2N维流体。
因此,速度场有2N个分量-每个q坐标和每个p坐标一个。 让他们

由等式(4)表示的发散概念很容易推广到任何数量的维度。 在三个维度上,这是相应方向上速度分量的导数之和。 同样,可以确定任意数量的尺寸。 在相空间的情况下,流的发散为2N个成员的总和:
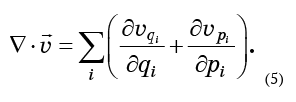
如果流体不可压缩,则此表达式应为零。 要计算它,您需要知道速度场的分量-当然,它们不过是相流体粒子的速度而已。
给定点处的流动矢量由该点处虚构粒子的速度确定。 换句话说
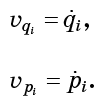
况且
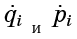
-这些只是输入汉密尔顿方程式(1)的量:
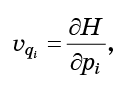
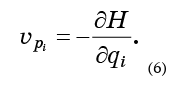
所有需要做的就是将方程式(6)代入公式(5)并得到
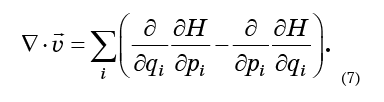
回顾该形式的二阶导数
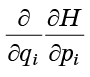
不依赖于微分的顺序,我们将理解等式(7)的各项完全成对地相互破坏:
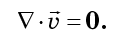
因此,相流体是不可压缩的。 在古典力学中,相流体的不可压缩性被称为Liouville定理,尽管它与法国数学家Joseph Liouville几乎没有关系。 它由伟大的美国物理学家约西亚·威拉德·吉布斯(Josiah Willard Gibbs)于1903年首次出版,也被称为吉布斯-里维尔定理。
我们通过要求进入任何小单元的流体总量为零来确定流体的不可压缩性。 还有另一个严格等效的定义。 想象一下某个时间点的液体量。 该体积可以具有任何形状:球形,立方体,滴状-可以。 现在,我们将跟踪该体积所有点的运动。 一段时间后,一滴液体将位于不同的位置并具有不同的形状。 但是,如果流体不可压缩,则液滴的体积将保持与原始体积相同。 因此,我们可以重新表述Liouville定理:
一滴相液体占据的
体积可以
及时保留 。
考虑一个谐波振荡器的示例,其中流体围绕参考点旋转。 显然,由于液滴的所有运动都减小到固态旋转,因此液滴保持了体积。 液滴的形状保持不变,但是谐波振荡器就是这种情况。 考虑另一个例子。 假设哈密顿量的形式为H = pq。
在您看来,这似乎与哈密尔顿法不同,尽管它是完全正确的。 我们得出运动方程:
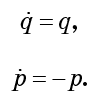
根据这些等式,q随时间呈指数增长,p以相同速度呈指数下降。 换句话说,流体将流体压向p轴,同时使流体沿q轴膨胀到相同程度。 任何下降沿q延伸,沿p收缩。 显然,液滴经历了巨大的变形,但是其相体积却没有变化。
Liouville定理是我们在第1讲中讨论的不可逆类型的最接近可想象的类似物。在量子力学中,Liouville定理被称为统一性的量子形式所代替。 统一性与我们在第1讲中讨论的更加相似,但这是下一期《理论最低要求》的主题。
»这本书的更多信息可以
在出版商的网站上找到»
感叹号»
摘录对于此博客的读者,优惠券可享受20%的折扣-
理论上的最低要求