将沙子倒在一个振荡的弹性板上,就可以看到
赫拉德尼图形的形成。 它们通常是物理现象的“自然之美”的一个例子,尽管它们背后是驻波共振激发的相当简单的物理学。 很少有人注意到这些图形的奇怪特征:它们上的线条避免了相交,好像有些力量排斥了它们。 让我们尝试了解这种排斥背后隐藏着什么样的物理学,以及它与混沌量子理论之间的关系。
驻波
众所周知,弹性体会产生相当复杂的振动,在此期间它们会收缩,拉伸,弯曲和扭曲。 然而,任何弹性体的振动都可以表示为彼此叠加的简单
法向振动的组合。 这就是一个简单的弹性体(一维拉伸线)的几种正常振动的样子。
每个正常振荡都由
驻波表示,该
驻波与行波不同,它静止不动,并具有其自身的空间振幅分布模式。 在该图中,可以区分出
波腹 -振荡振幅达到最大值的点和
节点 -振荡振幅为零的固定点。 另外,每个这样的波都以其
自己的频率振荡。 如您所见,在弦的情况下,驻波的振荡频率随着节点和波腹的数量增加而增加。
现在让我们看一个二维系统,其中一个例子是在刚性框架上拉伸的弹性薄膜。
圆形膜的正常振动看起来比弦的情况更为复杂,并且代替单个点节点,而有
节点线使膜固定。

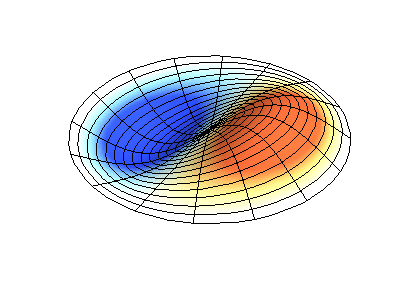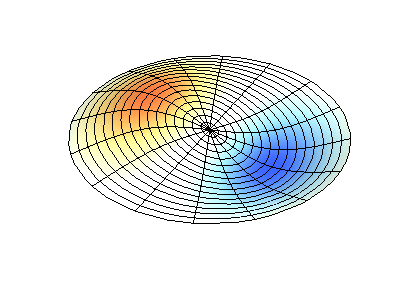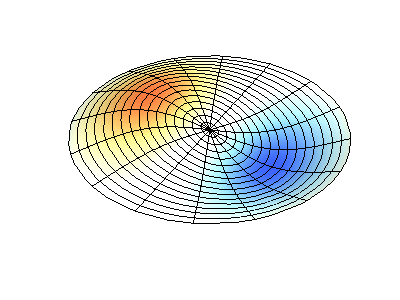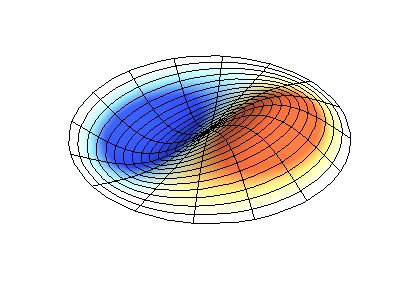


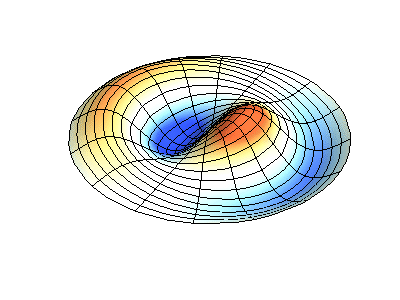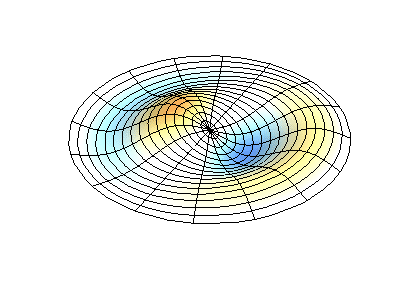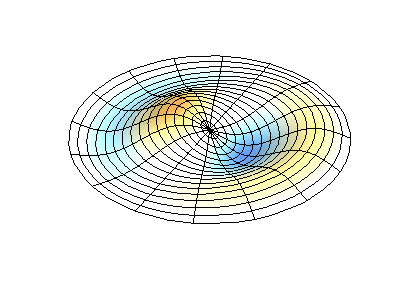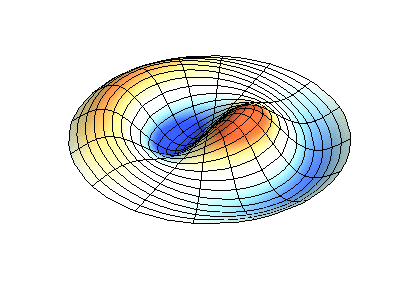
 具有固定边缘的圆形膜的正常振动。 来源绿色显示节点线。
具有固定边缘的圆形膜的正常振动。 来源绿色显示节点线。在圆形膜上,节点线(它们是沿半径的圆形和分段)可以成直角相交。 如果膜的边缘具有任意形状,则找到正常振动的频率以及它们的节点和波腹的模式就会变成只能使用计算机解决的问题。
膜上驻波振荡的振幅的轮廓,形式为带孔的正方形 , 科克雪花和小猫的表面 。描述弹性薄板振动的方程式与膜片的振动方程式不同,因为该膜片具有自己的刚度,而膜片仅由于外力作用而具有弹性和弹性。 但是,也存在一组正常振动,这些振动的图形基本上取决于边界的形状。
赫拉德尼数字
如上所述,在一般情况下,身体振动是在其中激发的整套正常振动的组合。
共振现象使您可以选择性地激发我们需要的一种正常振动-为此,我们需要使用外力使身体摆动,该外力的频率等于正常振动的固有频率。
下面的两个视频显示了获取Hladni人物的典型方案:弹性板的中央附着有机械振动发生器,其频率逐渐增加。 当振荡器频率共振地匹配这些振动的固有频率时(其左下角的视频中显示了固有频率),就会激发正常的板振动,它们具有节点和波腹的模式。
这是同一视频的版本,其中正常振动的频率可以通过耳朵进行估算。 这里有些漂亮。由于振荡板附近的气流将沙粒吹向驻波的节线,因此我们看到了结和波腹的图案
(*) 。 因此,
赫拉德尼的数字向我们展示了弹性板正常振动的节点线模式。吉他顶部甲板上的几个Hladni人物。 来源法向波的另一个例子是水面上的驻波。 它们用不同于板和膜振动方程的方程式描述,但是遵循相同的定性定律,在它们的帮助下,有可能获得Hladni图形的类似物。
各种形状的容器中水表面的微粒。 黑线表示2毫米的刻度。 来源经典混乱
因此,我们发现在圆形膜的情况下,理论上的节线是! -同时,在正方形或更复杂的板上的Hladni图形上明显相交,节点线避免相交。 为了理解这些模式的原因,我们将不得不简短地探讨一下混沌理论。
古典混沌是机械系统的特性,其特征在于其运动轨迹对初始条件变化的强烈依赖性。 这种关系也称为“
蝴蝶效应 ”。 在尝试预测天气时,可以找到一个混沌行为的生动例子:描述大气和海洋运动的方程系统由于原始数据的微小误差而导致指数增长,因此无法长时间进行足够准确的预测。
(**) 。
气象学家和数学家
爱德华·洛伦兹 (
Edward Lorenz )公开并广泛地使用了这种混乱现象,他们发现,从非常接近的初始条件开始的两种天气预报计算最初几乎是无法区分的,但是在某些时候,它们开始出现根本性的分歧。
Edward Lorenz进行了两次计算,从接近的初始值0.506和0.506127开始。 来源台球是最简单的系统,在该示例中可以方便地研究混沌,它是
台球 -平坦的表面部分,球可以沿着该部分滚动而不会产生摩擦,并且绝对弹性地弹跳出刚性壁。 在
混乱的台球中,球的
运动轨迹在一开始就略有不同,但随后却大不相同。 下图所示的
西奈台球是一个混沌台球的例子,它是一个矩形池,中心有一个圆形障碍物。 正如我们将看到的,正是由于这种障碍,台球变得混乱了。
西奈台球中的两个指数发散的球轨迹。 来源可积和混沌系统
非混沌的机械系统称为
可积分系统 ,以台球为例,您可以清楚地看到可积分系统与混沌系统之间的区别。
矩形和圆形台球由于其对称形状而可集成
(***) 。 球在这样的台球中的运动仅仅是两个独立的周期性运动的组合。 在矩形台球中,这些运动是在水平和垂直方向上从墙壁弹跳而来的,而在圆形运动中,这是沿着半径的运动和围绕中心的圆弧运动。 这种运动很容易计算,并且不会表现出混乱的行为。
可集成台球中的球轨迹。形状较复杂,不具有圆形或矩形高对称性的台球比较混乱
(****) 。 我们在上面看到的其中一个是西奈台球,其中矩形的对称性被中心的圆形夹杂物破坏了。 台球“体育场”和蜗牛帕斯卡尔形式的台球也经常被考虑。 球沿着非常复杂的路径在混乱的台球中运动,并且不会分解为更简单的周期性运动。
混沌台球“体育场”和“蜗牛帕斯卡”中球的运动轨迹。在这里,您已经可以猜到,在Hladni的图形中,线之间是否存在相交是由板块是可整合的台球形式还是混沌的台球形式决定的。 在下面的照片中可以清楚地看到这一点。
圆形板Hladni,展示了集成式台球的性能。 来源用台球“体育场”形式展示板Hladni的混沌台球的性质,小提琴和正方形的情况,其对称性被中心的圆形固定装置破坏(西奈台球的类似物)。 来源量子混乱
如何理解为什么结线之间的交点是由于台球的可整合性? 为此,我们需要转向
混沌的
量子理论 ,将混沌理论与振荡和波动的机理相结合。 如果在经典力学中,台球中的球被描述为沿着某个轨迹运动的物质点,那么在量子力学中,其运动被描述为服从
薛定er方程并从台球壁反射的波的传播。
量子台球中波的传播阶段。 最初,波集中在一个圆形脉冲中,并从左向右移动,然后传播并从壁上反复反射。 来源 动画形式相同,但初始条件略有不同。与膜和板的振动一样,描述量子台球的Schrödinger方程使人们能够以驻波的形式找到正常的振动,这些驻波具有节点线和波腹的特征性图案,每个振动和边界的形状各不相同。
混沌量子台球“ 帕斯卡尔的蜗牛 ”和“ 运动场 ”中驻波振荡幅度的分布示例。可积分和混沌量子台球中的驻波模式在质量上是不同的:可积分台球显示对称的,有序的驻波模式,而在混沌台球中,驻波的模式非常混乱,没有任何可见的模式(在本文的最后,我们将看到一些有趣的现象)。模式仍然存在)。
可积分圆形台球(上排)和帕斯卡蜗牛(下排)形式的混沌台球驻波中的振幅。 来源混沌台球中正常振动的奇异图片有时会作为单独研究的主题。 来源在节点线的模式上也看到质的差异:在可积分量子台球的情况下,我们看到
相互交叉的线的有序族,而在混沌台球中,这些线
通常不相交 。
上图:台球的可积分驻波的节点线(蓝色和红色区域之间的黑色线)。 下图:混沌台球中一个驻波的节点线- 体育场台球的四分之一 。相交还是不相交?
为什么混沌台球中的节点线不相交? 1976年,数学家
凯伦·乌伦贝克(Karen Uhlenbeck)证明了一个
定理,根据该
定理 ,通常来说,量子台球的驻波结线不应该相交。
以简化的形式
可以显示如下:假设两条节点线在一个点(
x 0 ,
y 0 )相交。 为此,确定驻波幅度对坐标的依赖性的函数
f (
x,y )必须同时满足以下三个条件:
1)在点(
x 0 ,
y 0 )处必须等于零,因为该点是节点。
2)如果从点(
x 0 ,
y 0 )沿第一条节点线的方向移动,则
f (
x,y )应保持等于零。
3)如果从点(
x 0 ,
y 0 )沿第二条节点线的方向移动,则
f (
x,y )也应保持等于零。
总共,我们对两个变量
f (
x,y )的函数施加了三个条件(或三个方程)。 众所周知,一个方程式不足以完全找到两个未知数
x和
y ,两个方程式已经足够解决这个问题,而三个方程式则太多了。 一般来说,除非有足够的幸运,否则针对两个未知数的由三个方程组成的系统将没有解。 因此,
节点线的交点只能作为例外而存在 。
在可集成的台球中,只会出现此类例外情况。 正如我们在上面看到的,它们的特殊属性-运动的可预测性,没有混乱,驻波的规则模式-是它们高度对称的结果。 相同的对称性确保同时满足节点线相交所需的三个条件。
现在让我们仔细看一下可积和混沌台球典型的Hladni人物的例子。 下图显示了
三种典型情况 。 在左侧,板的形状为圆形,因此相应的量子台球是可积分的,并且节线彼此相交。 在中心,板是矩形的,这也对应于一个可积分系统,但是,在中心的圆形安装略微违反了矩形的对称性,因此节点线不会在任何地方相交。 右侧显示了一个纯混沌系统的示例:一块四分之一的西奈台球形状的板(在右上角有一个圆形切口),节点线不再相交。
因此,
考虑到板的紧固性,板的形状越强,与集成台球的形状(例如圆形或矩形)不同,其上的节线相交越少 。
要获得漂亮的Hladni人物并在圆板上交叉的线条并不容易。 当使用中央安装座来激发振动时,整个系统的圆形对称性阻止了径向节点线的形成,因此我们只会看到无聊的一组圆(这种困难可以通过不从中心而是通过使用小提琴的弓形从板的边缘来激发振动来解决)。 如果将板固定在偏心位置,则Hladni图形将变得更加有趣,但是由于违反了圆对称性,该系统将不再可积分。
圆盘,中心安装。 圆盘,安装座偏离中心。 这是圆形和非圆形板的不同选择。最后,一个细心的读者可能会注意到:但是我看到有时结线即使在“混沌”板上也相交。 如果乌伦贝克定理禁止它们的交点,那怎么办?
首先,节点线可以避免相交,但是在此之前它们非常接近,以至于由于沙路的宽度有限,在我们看来似乎存在相交。 其次,在可积和混沌系统之间,实际上并没有明确的界限。
节点线-它们将黑白区域分开-在可积分和混沌量子台球(左和右)中,在中间拟可积分情况下(在中间)。 在中间情况下,节点线有多个交叉点,而在混乱情况下根本没有。 来源在经典的混沌理论中,著名的
Kolmogorov-Arnold-Moser理论致力于解决这一问题。 她说,如果稍微破坏了可积系统的对称性,它将不会立即表现出混乱的行为,但是在大多数情况下,将保留其可预测的运动性。 在混沌和Hladni图的量子理论层面,这表现为以下事实:在某些地方保留了节点线的交点。 这或者在台球的特别对称的点处发生,或者在远离干扰源的地方发生,这违反了可积分系统的对称性。
还有什么
混沌的量子理论还有什么有趣的呢? 对于感兴趣的读者,我将提到三个不再与Hladni人物直接相关的问题。
1)该理论研究的一个重要现象是混沌系统的
普遍性 。 可以发生正常振动的绝大多数系统都是混沌的,而所有这些系统-不论其物理性质如何! -遵守相同的法律。 普遍现象用相同的公式描述了完全不同的系统,它本身非常漂亮,并提醒了物理世界的数学统一性。
不同物理性质的混沌系统中正常振动的相邻频率之间的距离统计,到处都用相同的通用Wigner-Dyson公式描述。 来源2)混沌台球的正常振动模式具有一个有趣的特征,称为
“量子疤痕” 。 我们已经看到,混沌台球中的球的路径通常看起来非常混乱。 但是也有例外-这些是
周期性轨道 ,是相当简单且短的闭合轨迹,球沿着该轨迹进行周期性运动。 量子疤痕被称为沿周期轨道驻波的急剧增厚。
台球“体育场”中的量子疤痕,沿着红色和绿色线所示的周期性轨道运行。 来源3)到目前为止,我们已经讨论了二维系统。 如果我们考虑波在三维空间中的传播,那么在这里也会出现节点线,沿着该节点线,振荡幅度为零。 当研究玻色凝聚和超流动性时,这一点尤为重要,在这种情况下,成千上万的原子作为单个“
物质波”运动 。
例如,有必要对三维空间中物质波的节点线结构进行分析,以了解量子湍流如何在超流体系统中产生和发展。玻色凝析物中站立的“物质波”的节线的三维结构纠结。源。(*)如果倒在板上的颗粒尺寸足够小,则它们将不被吹到驻波的波腹,而是吹到驻波的波腹,如本实验工作所示。
(**) «» «» , : – , , . .
(***) – . , , , .
(****)更准确地说,台球属于可积分或混沌的取决于运动的独立积分的数量-随时间推移而持续存在的数量。集成的台球具有两个运动积分,在二维系统中,这足以对运动方程进行精确的解析解。混沌的台球只有运动的一个组成部分-球的动能。