宇宙常数和宇宙的创造
关于宇宙，有两个特别痛苦的未解之谜，其中一个与它的最终命运有关，第二个-从一开始，就吸引了数十年的宇宙学家。 科学界一直认为这两项任务是相互独立的，但是如果不是的话该怎么办呢？
第一项任务与所谓“黑暗能量”的存在有关，如今，它加速了宇宙的膨胀，并最终决定了它的最终命运。 理论家说，暗能量的作用可以通过在爱因斯坦方程中引入一个称为“宇宙常数”的新术语来解释。 但是，为了使这种解释起作用，宇宙常数必须具有一定的非常小的值。 在自然单位中，它由一个单位除以由123位数字组成的数字确定！ 该常数的值的解释是理论物理学中最困难的问题之一。
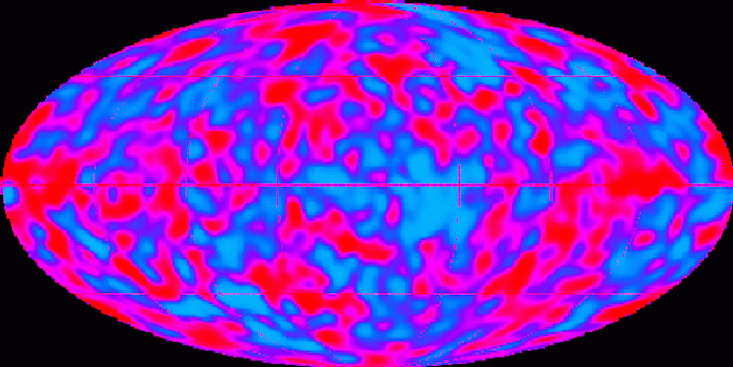CMB变化表明早期宇宙的密度波动第二个问题与另一个定义宇宙的重要数字以及与结构（例如星系和星系组）的形成有关。 我们知道，尽管早期的宇宙非常均匀，但其密度的波动很小，这成为我们今天所看到的宇宙结构的根本原因。 为了与我们的观察一致，这些波动必须具有一定的大小和形状。 这些波动如何在宇宙演化的最早阶段出现，以及它们的形状和大小，也是宇宙学同样令人惊奇的谜。
考虑到普遍接受的宇宙学方法，这两个数字（宇宙常数的大小和初始扰动的大小）不相关。 毕竟，其中一个涉及宇宙的最早阶段，第二个阶段涉及最晚的阶段，它们之间的间隔时间为140亿年。 而且，标准宇宙论没有根据基本原理来解释这些价值。 普遍接受的宇宙模型没有提及宇宙常数的数值，也没有预测完全不同的数值。 关于初始扰动的大小，最流行的方法是从描述通货膨胀的模型类别中获得该值，通货膨胀是宇宙存在初期的快速增长时期。 通货膨胀模型的问题在于可以对其进行调整以产生几乎任何结果，这就是为什么它们缺乏预测能力的原因。
在我最近与苏黎世瑞士高级技术学校的女儿Hamsa Padmanabhan和Tomalla Fellow一起进行的工作中，这两个数字都与宇宙发生有关-宇宙的产生-并解释了它们的确切含义。 我们最近发表在《物理学快报B》上的工作表明，宇宙常数的存在及其微小的价值可以表示为时空信息内容的直接结果[Padmanabhan，T.＆Padmanabhan，H.宇宙信息，宇宙学常数和原始扰动的幅度。 Physics Letters B 773，81-85（2017）]。 此外，分析为早期宇宙的小波动的大小和形状提供了正确的值。
这些基本常数之间的显着联系对于我们对宇宙的理解至关重要。 特别是，它改变了我们对“大爆炸”的理解，并消除了在宇宙早期阶段需要通货膨胀的时期。
大爆炸可能是标准宇宙学最著名的特征。 但是他也不是真正需要她的人。 用爱因斯坦的方程式描述的宇宙经典模型，在大爆炸的条件下，在无限的密度和温度下停止工作，这就是物理学家称之为奇点的情况。
但是，如果没有奇点怎么办？ 自1960年代以来，物理学家一直在努力描述没有大爆炸的宇宙，试图将引力理论和量子理论结合在一起，称为“量子引力”。 物理学家约翰·惠勒（John Wheeler）和布莱斯·德威特（Bryce DeWitt）最早将这些思想应用于宇宙的假设教义学阶段，在该阶段，时空的概念尚未从一个未知的结构中出现。 这导致了量子宇宙学的出现，物理学家试图用量子语言描述宇宙的简单玩具模型的动力学。 不用说，在过去的几十年中，突然之间出现了几种不同的尽管相关的描述几何前阶段的想法。 使它们团结在一起的是，没有任何奇点的经典宇宙是通过从几何前阶段到爱因斯坦方程式描述时空的一系列转换而出现的。 构造此类描述的主要困难在于，我们没有一个完整的量子引力理论，无法使我们对几何前相进行详细建模。
爱因斯坦称自己对宇宙常数的沉迷数次是他方程中的重大错误。 今天，物理学家认为它具有积极的意义。我们介绍来帮助避免这种技术复杂性的关键要素是空间信息的概念。 最近，越来越多的人认为信息在描述物理学中起关键作用。 在某些情况下，科学家试图将量子理论和引力的原理结合在一起时，例如在量子黑洞的研究中，这种现象就出现了。 同样，在这些模型中的某些模型中，全息技术很有意思，它指出大区域的信息内容可以与其边界的信息内容相关。 但是，不幸的是，在不同情况下信息的数学描述是不同的，并且尚未找到适用于所有情况的统一原理。 因此，要将信息的概念应用于整个宇宙，我们首先需要为它提出一个物理上合适的定义。
我们使用的空间信息的定义可以用类比来描述。 当一块冰融化并变成水时，就会发生从固态到液态的相变。 实际的相变过程可能非常复杂，但是冰原子的总数将与水原子的数目相同。 此数字确定在相变期间不改变的系统自由度的数量。 以完全相同的方式，导致宇宙出现的相变可以用将几何前阶段的自由度数与经典时空固有量相关的数字来描述。 使用我们称为CosmIn的数字，我们可以将宇宙的两个相结合起来，并绕开整个量子引力模型的复杂性。
cosmin作为一个物理上可观察的数字，必须是有限的。 在没有奇异性的情况下，我们认为所有物理量都应是有限的。 另外，我们能够证明，只有在宇宙存在后期，宇宙经历加速的扩张阶段时，cosmin才是有限的-就像我们今天所观察到的那样。 这种联系不仅表明存在宇宙学常数的根本原因，而且还表明了计算其数值的方法-如果我们知道宇宙胺的值。
可以使用周期性出现在不同量子引力模型中的结果来确定宇宙的几何前或量子引力相中的cosmin值。 事实证明，从量子引力相转移到经典相的信息总量应该等于一个简单数字：4π，即单位半径球体的面积。 利用这一事实，我们可以将宇宙常数的数值与能级联系起来，在该能级上，宇宙从量子引力相转移到经典相。
这种跃迁的能量尺度可能与我们宇宙的第二个神秘特性有关：早期宇宙中微小的量子涨落的大小，该微小涨落生长并形成了我们今天所看到的星系和银河星团。 一种用于计算这些波动大小的流行系统使用宇宙的膨胀模型，该模型描述了宇宙经过难以置信的大而快速的膨胀。 但是，有许多通货膨胀模型，它们有很大的不同，它们可以给出任何期望的值。 还要注意的是，初始波动的形状是由爱德华·罗伯特·哈里森（Edward Robert Harrison）在1970年获得的（并且由雅各布·泽尔德维奇（Jacob Zeldovich）独立获得），被称为哈里森-泽尔德维奇谱。 但是人们忘了指出，哈里森在发明通货膨胀模型之前十多年前就取得了他的成果！
我们的模型允许我们将量（宇宙常数的值和初始波动的大小）与几何前期宇宙经历相变并成为我们所居住的经典宇宙的能级相关。 而且要注意的是，当我们选择正确的能级时，对于这两个值，我们都会获得正确的观测值。 这导致我们在宇宙常数，初始涨落幅度和宇宙之间建立代数关系。 我们可以使用观测到的宇宙学参数翻转这种关系，并检查cosmin值是否真的为4π。 该理论完美地通过了测试； 我们发现，从观测值确定的余数为4π，精度为1/1000。
令人惊讶的是，认为彼此无关的宇宙学参数的复杂组合具有如此简单的含义。 一种常见的方法是将这种关系视为随机巧合。 我们相信她在告诉我们关于我们宇宙的深刻而美丽的东西。
我们相信，我们首次尝试将宇宙学常数的数值与早期宇宙的波动大小联系起来，并从一个没有可调整参数的模型中获得这两个值，并将它们与宇宙开始存在的能级相关联。
所有这些想法都存在于一个更通用的量子引力平台上，尽管物理学家已经发展了将近五十年，但仍然没有这个理论。 我们模型的优点之一是它不需要量子引力的细节。 但是她提供了关于量子引力的性质和时空结构的两个重要线索。 首先，她说时空必须表示为微观自由度以及原子组成的物质。 其次，她认为正确的宇宙起源理论应该包括从几何前阶段到古典阶段的相变。
这些技巧可以回答一个关键问题：为什么经过几十年的研究，理论家们却没有将引力理论和量子理论结合起来？ 我们认为，最好用另一个类比来解释。 我们知道流体动力学是通过一组方程式表达的一致的物理理论。 如果我们以它们为基础并将量子理论的原理应用于它们，我们会发现一个有趣的新现象-例如，声子（振动量子）及其相互作用。 但是，使用这种方法，我们将无法获得物质的量子结构。
有证据表明，在这种意义上描述重力的方程与流体动力学相似。 换句话说，使用量子理论原理重新构造描述重力的方程式类似于将量子原理应用于流体动力学方程式。 我们不会以这种方式发现时空的量子结构-我们相信由于这个十年，量化爱因斯坦理论的尝试以失败告终。
相反，我们需要重新思考引力的本质，并了解引力对时空微观结构的影响。 物理学家
路德维希·玻尔兹曼 （
Ludwig Boltzmann）使用这种方法来理解温度现象需要由离散的自由度（即原子）组成的物质概念。 实际上，玻尔兹曼说，如果某些东西可能很热，它应该包含微观的自由度。
时空也可能有温度，对某些观察者来说似乎很热。 这个想法的产生归功于雅各布·贝肯斯坦（Jacob Beckenstein）和史蒂芬·霍金（Stephen Hawking）在黑洞背景下的工作。 此后不久，在70年代中期，Bill Unrich和Paul Davis的工作表明，这是时空的主要特征。 通过将玻尔兹曼范式与时空（像普通物质）一样炙手可热这一事实结合在一起，可以得出结论，时空必须具有内部自由度，就像物质中的原子一样。 近年来，已经出现了支持该结论的理论证据[Padmanabhan，T.时空原子和宇宙学常数。 物理学杂志：会议系列880，012008（2017）]。 这种观察包含了理解时空微观结构的关键，这很快就导致了惊人的结果。
首先，时空站点的演变可以根据位于该站点边界内的自由度（或等效地，信息内容）来描述。 其次，重力对零能级的变化不敏感。 在爱因斯坦的理论中，重力是绝对能量的原因，这就是为什么几乎不可能计算宇宙常数的原因。 但是对于基于信息内容的范例，事实并非如此。 第三，信息方法表明我们不应该根据爱因斯坦方程的某种解来想象宇宙演化。 这些方程式来自一组更精确的方程式，描述了时空的量子自由度[Padmanabhan，T。我们真的了解宇宙吗？ Compend Rendus Physique 18，275-291（2017）]。
我们的宇宙模型验证了这种信息方法，它为我们提供了一个新颖的，生动的宇宙图景，类似于一块装有热源的大冰块。 一个热源将周围的冰融化，产生一部分水膨胀，达到局部热力学平衡。 由于从内部加热了一块冰，因此在更大范围内，更接近相边界，分子尚未达到平衡。 有趣的是，这与我们宇宙的行为非常相似。 水的图类似于可观测的宇宙（由爱因斯坦的理论描述）。 它被一个预几何相包围（类似于冰），至今为止还不知道它的量子引力定律。 大爆炸的想法消失了，取而代之的是沿其边界从一个阶段过渡到另一个阶段。 通货膨胀时期的需求也消失了。
整个平台简单而优雅，因为它由一个参数来描述：早期宇宙从预几何到爱因斯坦几何的相变的能级。 这不同于包含许多参数且没有预测能力的常规通胀模型。 我们的模型没有使用未经验证的物理学。 我们唯一得出的假设是，宇宙的含量应等于4π（单个球的表面积）。
这项工作开辟了三个新的研究领域。 首先，她邀请我们在各种量子引力模型中研究几何前期的物理学。 其次，它提供了一个机会来研究在这项工作中使用的空间信息的概念，并尝试将其与在其他上下文中使用的其他类似思想联系起来。 第三，它强化了时空包含更多基本的自由度（就像物质由原子组成一样）的观点，并鼓励我们以与研究
凝聚态物理中物质的各个阶段相同的方式研究时空的各个阶段。
Tanu Padmanabhan是印度大学间天文学与天体物理学中心的教授。