一位杰出的数学家透露了他在研究几千年历史的数学问题方面的成功与物理学概念相关的细节。
 米尼翁·金(Mignon Kim)
米尼翁·金(Mignon Kim)数学充满了大多数人从未听说过的怪异数字系统。 其中一些甚至将难以想象。 但是
有理数是每个人都熟悉的。 这些是用于计算对象和分数的数字-我们从小学就知道的所有数字。 但是在数学中,有时最简单的东西最难理解。 它们很简单,就像光滑的墙壁,没有裂缝和突起,也没有您可以抓住的其他明显特性。
牛津大学的数学家
Minion Kim对哪个有理数适合求解某种方程的问题特别感兴趣。 这个问题激发了数以千计的理论专家。 他们几乎没有在解决方案方面取得任何进展。 当一个问题研究了这么长时间而没有答案时,可以得出结论,提出该问题的唯一方法是提出一个全新的想法。 金正是如此。
“虽然过去3000年来我们一直在致力于这项技术,但是没有多少技术可以使用。 因此,当有人提出一种真正新颖的方法时,它就会引起人们极大的兴趣,而Mignon正是这样做的,”威斯康星大学麦迪逊分校的数学家约旦·埃伦伯格说。
在过去的十年中,Kim描述了一种在看似混乱的有理数世界中寻找模式的全新方法。 他在文章和会议中描述了这种方法,并将其传递给现在自己继续进行这项工作的学生。 但是他总是保存一些东西。 他的愿景使他的思想焕发了生命,他的愿景不是基于纯粹的数字世界,而是基于从物理学中借来的概念。 对于金恩而言,理性的决定让人想起光的轨迹。
 数学对象,一个三孔圆环,装饰在牛津大学的金董事会上。
数学对象,一个三孔圆环,装饰在牛津大学的金董事会上。如果这种联系看起来很棒,那么即使对于数学家来说也是如此。 因此,Kim很长时间没有透露她的详细信息。 他说:“我隐藏了它,因为多年来我一直对与物理学的联系感到困惑,” “数论专家是非常实践的人,物理学的影响有时使他们怀疑数学。”
但是现在金说他准备分享他的愿景。 “我认为变化只是衰老的症状!” -在我们交换以撰写此故事的首批信件之一中,金满53岁的金写道。
他最近举行了一次会议,召集了数论和弦论方面的专家。 他还草拟了一些文章草稿,开始描述他对数学界的启发,而不是习惯使用与物理世界的直接类比来思考数字。
仍然只有一个障碍-金恩尚需解决的数学类比的最后一部分。 他希望通过邀请其他人,特别是物理学家分享他的视野,他将获得完成这项工作所必需的帮助。
古代谜语
方程的有理解会积极吸引人的思想。 它们带来的满足感,类似于您从适当的拼图中获得的收获。 因此,它们是最著名的数学假设的英雄。
有理数包括整数和任何可以表示为两个整数之比的数字,例如1 --4或99/100。 数学家对解决Diophantine方程的有理数特别感兴趣,例如有整数系数的多项式方程,例如x
2 + y
2 =1。他们以数学家
Diophantus的名字命名,后者是在公元3世纪在亚历山大研究的。
在一般情况下,很难找到有理解,因为它们不遵守任何几何规律。 取方程x
2 + y
2 =1。它的
实数解形成一个圆。 删除圆上所有不能表示为分数的点,将仅保留不构成此类整洁对象的理性决定。 有理数解在圆周上看起来是随机分布的。
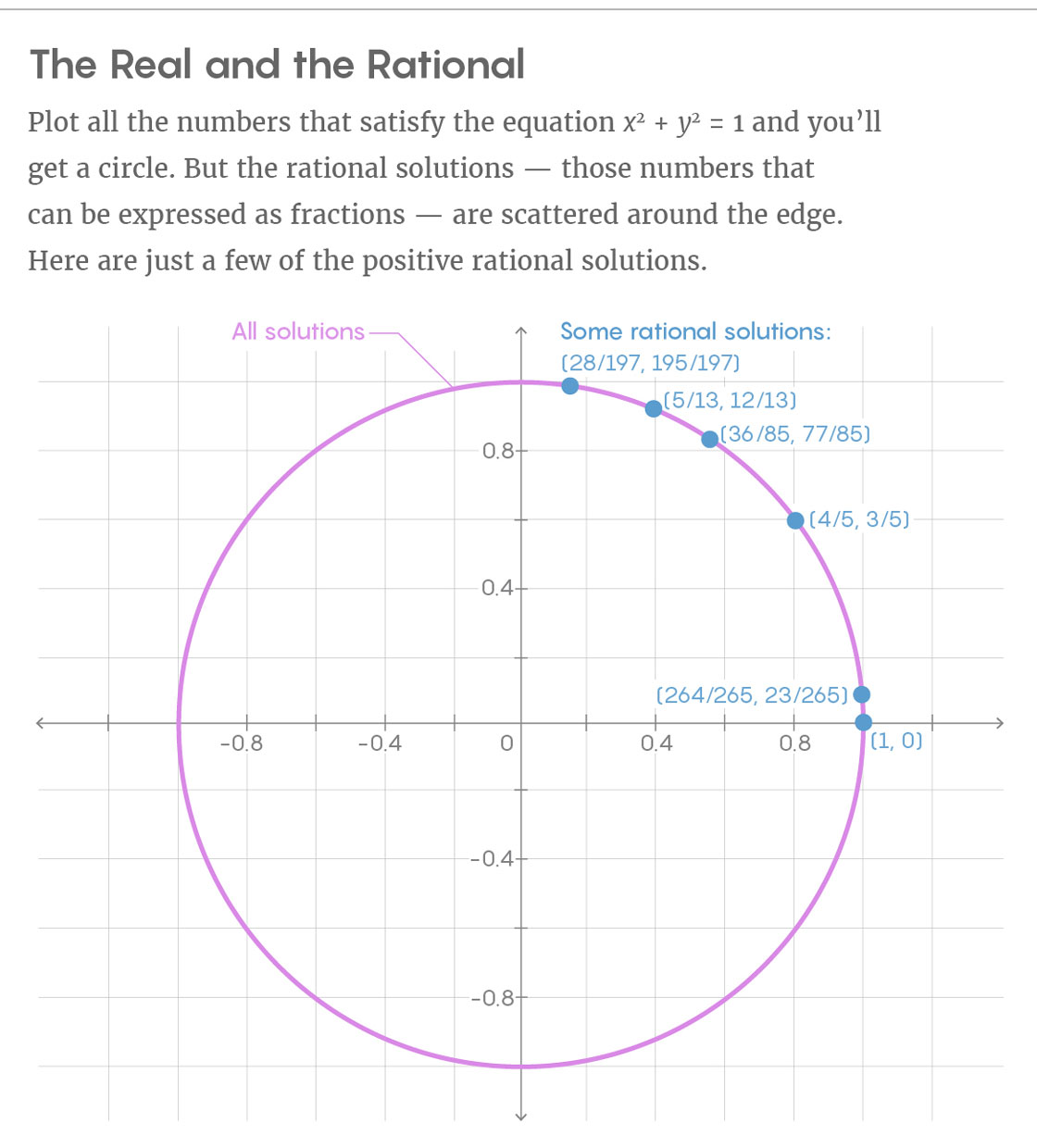
“点必须遵循以具有合理坐标的条件根本不是几何的。 金说,不可能写出一个有理点必须满足的方程。
找到一个甚至多个合理的解决方案通常很简单。 但是不喜欢轻描淡写的数学家对寻找所有合理的解决方案更感兴趣。 而且这要复杂得多。 很难做到,即使是关于理性决定数量的微小陈述的证据也足以通过数学。 1986年,
Gerd Falting赢得了最高数学奖
菲尔兹奖 ,主要是因为证明
了Mordell假设 ,该
假设说某些Diophantine方程只有有限数量的有理解。
法尔廷的证明是数论的转折点。 而且也被数学家称为“无效证明”,因为它没有给出合理解的确切数量,也没有找到它们。 从那时起,数学家一直在寻找下一步的方法。 有理点在规则方程图上看起来是随机的。 数学家希望通过改变思考问题的环境,可以使这些观点看起来像是可以用某种确切方式描述的有意义的组合。 问题是众所周知的数学领域没有提供这样的背景。
 金在牛津的办公室
金在牛津的办公室“为了从理性的角度获得有效的结果,显然需要一种新的想法,”埃伦伯格说。
关于这种想法的性质,现在有两个主要假设。 其中一位来自日本数学家
本月伸一(Shinichi Motizuki) ,他于2012年在京都大学教授的页面上发表了数百页的
复杂而创新的数学著作 。 五年后,这项工作在很大程度上仍然难以理解。 金的另一个新想法来自金,他试图在扩展的数字上下文中想象有理数,在这些数字中它们的隐藏模式开始出现。
对称解决方案
数学家经常说,一个物体越对称,研究它就越容易。 因此,他们希望将双色子方程的研究放在比自然出现此问题的对称性更高的条件下。 如果成功,他们将能够使用新发现的对称性来跟踪所需的有理数。
要了解对称如何帮助数学家解决问题,请想象一个圆圈。 也许您的目标是识别圆上的所有点。 对称性很有帮助,因为它创建了一个地图,使您可以从已知点移动到仍然需要发现的点。
想象一下,您已经在圆底找到了所有有理点。 由于圆具有镜像对称性,因此这些点可以向上反射(在所有y坐标处都改变符号),并突然从顶部获得所有点。 圆通常具有非常丰富的对称性,以至于要搜索圆上的所有点,您只需要找出一个点的位置,然后将其与关于圆对称性的知识相结合即可:您只需要将圆的无限旋转对称性应用于起点即可。
但是,如果与您一起使用的几何对象的正确性要差得多,例如随机摆动的路径,则您将不得不做很多工作来分别确定每个点-您将不会具有对称关系,当出现以下情况时,它们可以标记未知点帮助著名。
数值集也可以具有对称性,并且集合中的对称性越多,就越容易理解-您可以应用对称关系来检测未知值。 具有某些对称类型的数字形成一个“组”,数学家使用该组的属性来理解其中包含的数字。
该方程的许多有理解都不必具有对称性,也不必组成一个组,这就是为什么数学家每次尝试寻找一个解都面临着不切实际的任务。
从1940年代开始,数学家开始研究在更对称的条件下安排Diophantine方程的方法。 数学家Claude Chabauty发现,在他创建的更大的几何空间内(使用称为
p-adic数字的扩展数字宇宙),有理数形成了它们自己的对称子空间。 他采用了该子空间,
并将其与Diophantine方程图
结合在一起 。 他们的交点证明是方程的有理解。
在1980年代,数学家
罗伯特·科尔曼(Robert Coleman)指定了Chaboti的作品。 在接下来的几十年中,Coleman-Chaboti方法是数学家找到Diophantine方程的合理解的最佳数学工具。 但是,只有当方程的图形与较大空间的大小按一定比例相关时,它才起作用。 断裂时,很难准确地找到方程曲线和有理数的交点的位置。
加利福尼亚大学圣地亚哥分校的数学家Kiran Kedlaya说:“如果曲线处于有很多合理点的环境中,它们就会开始积累,并且您很难区分曲线上的哪些点。”
然后金进入。 为了扩展Chaboti的工作,他想找到一个更大的空间来研究Diophantine方程—一个有理数更加零散的空间,这使我们能够研究带有大量Diophantine方程的交点。


空间的空间
如果您需要更大的空间,并且对如何使用对称性进行定位有一些提示,那么物理将适合您。
通常,数学意义上的空间是具有几何或拓扑结构的任何点集。 一千个由意愿散布与否的点不会形成空间-它们不会通过结构连接在一起。 但是作为点的连接组织的领域已经是空间。 就像我们居住的圆环,二维平面或时空一样。
除了这些,还有更多的异国情调的空间可以想象为“空间空间”。 最简单的例子:假设您有一个三角形-这就是空间。 现在想象所有可能的三角形的空间。 其中的每个点都代表一个特定的三角形,该点的坐标由该点表示的三角形的角度确定。
这样的想法在物理学中通常是有用的。 在广义相对论的框架内,空间和时间在不断发展,物理学家认为空间和时间的每种配置都是所有时空配置中的一个点。 空间的空间也出现在物理学家称为量规不变性的区域中,并处理叠加在物理空间上的场。 这些场描述了当在太空中移动时电磁力和重力等力如何变化。 可以想象,在空间的每个点上,这些字段的配置都稍有不同-并且所有这些不同的配置在更高维度的“所有字段的空间”中形成了点。
这个物理学领域的空间类似于金正恩关于数论的建议。 要理解这一点,请想象一束光。 物理学家代表光在高维场中移动。 在这个空间中,光将遵循一条路径,该路径遵循最小阻力的原理,并最小化从点A到点B所需的时间。此原理解释了为什么光从一种材料移动到另一种材料时会弯曲-弯曲的路径可将时间最小化费用。
物理学中出现的较大空间具有其他对称性,这些对称性在它们表示的任何空间中都不存在。 这些对称性引起人们对某些点的注意,例如,专注于使时间最小化的路径。 可以在其他点(例如,在对应于方程的有理解的点)上强调以不同方式和不同上下文构造的相同对称性。
将对称与物理联系起来
在数论中,没有可以跟踪的粒子,但是它具有时空之类的东西,它提供了一种绘制路径并创建所有可能路径的空间的方法。 正如他上周在海德堡举行的一次数学物理学会议上所解释的那样,金正日根据这种基本对应关系制定了一些方案,其中“寻找光的轨迹和寻找丢番亭方程的有理解的问题是同一问题的两个方面”。
Diophantine方程的解形成空间-这些是由方程定义的曲线。 这些曲线可以是一维的,例如圆形,也可以是多维的。 例如,如果您构建了双色子方程x
4 + y
4 = 1的复杂解,则会得到一个带有三个孔的圆环。 这样的圆环上的有理点没有几何结构-这就是为什么很难找到它们的原因-但可以将它们与拥有这种结构的多维空间中的点进行比较。
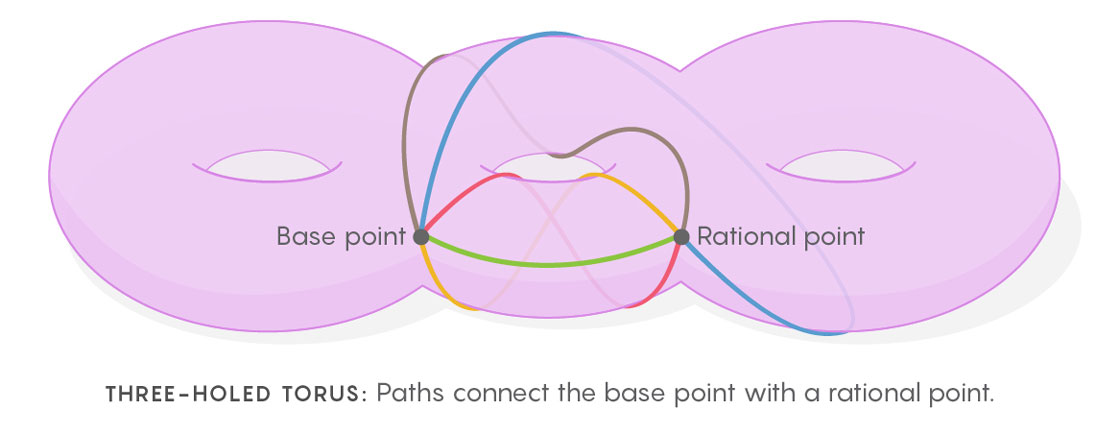
Kim创造了这种多维的空间空间,设想了可以在圆环(或定义方程式的空间)中绘制闭合曲线的方式。 绘制曲线的过程如下所示。 首先,您需要选择起点,然后从该点到其他任何点画一个循环,然后返回到第一个。 现在重复此过程,绘制连接基点和圆环的所有其他点的路径。 您将获得所有从基点开始和结束的可能循环的灌木丛。 这组循环是数学的一个重要中心,称为空间的
基本组 。
圆环上的任何点都可以用作起点。 每个点都有一个唯一的路径丛生。 这些路径集合中的每一个都可以表示为多维“所有路径集的空间”中的一个点(所有可能的三角形的空间)。 这种空间空间在几何上非常类似于物理学家在轨距不变性理论中构建的空间:当您从圆环上的一个点移动到另一点时,路径组的变化方式与从一个点到圆环的变化方式非常相似。在现实空间中的另一个。 该空间空间具有圆环本身不存在的其他对称性。 尽管圆环上的有理点没有对称性,但是如果我们进入所有路径集的空间,我们可以发现与有理数相关的点之间的对称性。 您将获得以前不可见的对称性。
“我有时说“潜算术对称”编码在这些路径中,这与规范不变性理论的内部对称非常相似,”金说。
与Chaboti一样,Kim通过在他们创建的较大空间中探索交点来找到合理的解决方案。 他使用该空间的对称性到达相交点。 他希望开发出可以精确定义这些点的方程式。
在物理环境中,人们可以想象一束光线可以通过的所有可能方式。 这是您的“所有路径的空间”。 物理学家对此空间中与最小化路径相对应的点感兴趣。 Kim认为,与从有理点发出的路径的灌木丛相对应的点具有相似的性质-也就是说,这些点将考虑Diophantine方程的几何形式时出现的某些性质减至最小。 他只是还没有弄清楚这个属性可能是什么。
他在给我的一封信中写道:“我开始试图寻找的东西”是数学上的最小阻力原则。 “我还没有找到它,但是我确信它存在。”
不确定的未来
在过去的几个月中,我描述了金的愿景,他的灵感来自物理学,几位数学家都是他对数论的贡献的拥护者。 但是当得知他的工作如此详细时,他们就迷路了。
“作为代表量的理论家,如果向我展示小黄人的所有惊人成就,并问他们是否受到物理学的启发,我会说:你在说什么?” -艾伦伯格说。
到目前为止,金在他的任何作品中都没有提到物理学。取而代之的是,他撰写了有关被称为“ Selmer变体”的对象,并研究了所有Selmer变体中Selmer变体之间的关系。数论专家对此很熟悉。但是对于Kim而言,它们始终只是某些物理对象的另一个名称。金说:“应该有一种利用物理思想解决数论问题的方法,但是我们还没有考虑到如何创建这样一个平台的方法。” “我们处于一种对物理学的理解已经非常完善的状态,许多数论专家对此都感兴趣,以便采取下一步行动。”Kim方法的主要障碍是找到一些措施来最小化所有循环集的空间。在物理世界中,这种方法看起来很自然,但是在算术中却没有明显的意义。即使是密切关注金正日工作的数学家也不确定他是否可以找到他。“我认为Kim的计划将为我们做很多很棒的事情。哈佛大学数学物理教授Arnav Tripathy说:“我认为我们不会像Mignon所想的那样清楚,即有理数点是否是算术量规理论的经典解决方案。”今天,物理学的语言几乎与数论的实践不相交。金相信这几乎肯定会改变。四十年前,物理学,几何学和拓扑学几乎没有共同之处。然后在1980年代,几位数学家和物理学家(现已成为重要人物)找到了使用物理学研究形式性质的确切方法。经过这一发展,该领域发生了变化,并且没有恢复到以前的方法。“如今,几乎不了解物理学就几乎不可能对几何和拓扑感兴趣。我很确定,在未来15年内,数字理论也将发生这种情况。“所有连接都是非常自然的。”