...并通过一个真实的例子学习与以太坊开发人员工具一起工作。
零部分：物体进入视野
我刚刚完成了有关以中文开发基于分散的以太坊为基础的应用程序的全过程的演讲。 我在业余时间给了它，以提高中国开发人员社区中有关区块链和智能合约的知识水平。 在工作中，我与几个学生交了朋友。
在课程结束时，我们突然发现自己被这些生物包围：
图片来自cryptokitties.co就像大多数遇到这种现象的人一样，我们也无法抗拒这些可爱的密码创作，并很快对游戏沉迷。 我们喜欢引进新的猫，甚至用
加密猫方法代替
了小鸭方法。 我认为沉迷于游戏是有害的，但在这种情况下不会如此，因为对繁殖小猫的热情很快使我们想到了一个问题：
某些加密猫如何获得其基因集？
我们决定专门在星期六晚上寻找答案，我们认为我们在软件开发方面取得了一些进展，该软件使我们能够在新生婴儿出生前确定其基因突变。 换句话说，该程序可以帮助您检查并确定适合猫妈妈受精的时间，从而获得最有趣的可能突变。
我们发布此材料是希望它能作为所有人的入门文章，以了解非常有用的以太坊开发工具，就像加密小猫自己允许许多不熟悉区块链的人加入加密货币用户的行列一样。
第一部分：饲养小猫的高级逻辑
首先，我们问自己：加密小猫的诞生如何？
为了回答这个问题，我们使用了出色的Etherscan区块链导体，它不仅使我们“研究块的参数和内容”，还能做更多的事情。 因此，我们发现了CryptoKittiesCore合同的源代码：
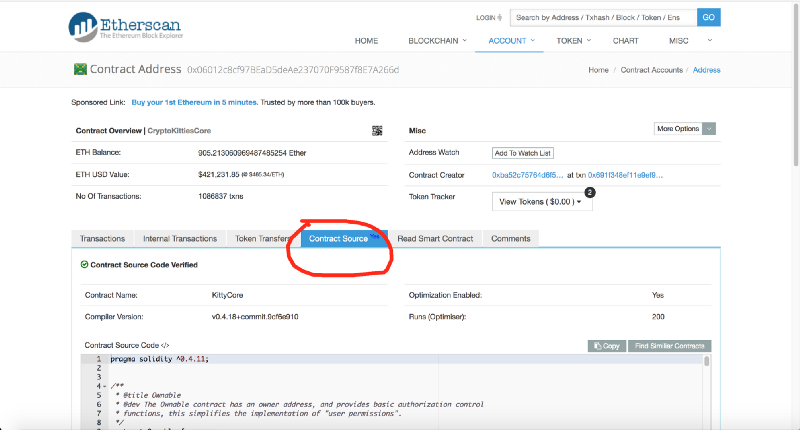https://etherscan.io/address/0x06012c8cf97bead5deae237070f9587f8e7a266d#code请注意，扩展合同实际上与赏金计划中使用的合同略有不同。 根据该代码，分两个步骤形成了一只小猫：1）母猫受猫的受精； 2）再过一会，当水果的成熟期结束时，将调用GiveBirth函数。 此功能通常由某个进程守护程序调用，但是，如您将在后面看到的，要获取有趣的突变，您将需要正确选择小猫出生的区域。
function giveBirth(uint256 _matronId) external whenNotPaused returns(uint256) { Kitty storage matron = kitties[_matronId];
在上面的代码中，您可以清楚地看到刚出生的小猫的基因是在出生时通过调用geneScience外部智能合约中的mixGenes函数确定的。 该功能具有三个参数：母亲基因，父亲基因和准备好产猫的块数。
您可能会有一个逻辑问题，为什么在怀孕时就不能确定基因，就像现实世界中那样？ 正如您在随后的叙述中所看到的，这使您可以优雅地捍卫预测和破译基因的尝试。 这种方法消除了在区块链中记录猫妈妈怀孕的事实之前100％准确预测小猫基因的可能性。 即使您找到负责混合基因的确切代码，也不会给您带来任何好处。
尽管如此，一开始我们还不知道这一点，所以让我们继续。 现在我们需要找出geneScience合同的地址。 为此，请使用MyEtherWallet：
基因科学合同地址合同字节码如下所示：
0x60606040526004361061006c5763ffffffff7c01000000000000000000000000000000000000000000000000000000006000350416630d9f5aed81146100715780631597ee441461009f57806354c15b82146100ee57806361a769001461011557806377a74a201461017e575b600080fd5b341561007c57600080fd5b61008d6004356024356044356101cd565b604051908152602001604051809........
从他的外表来看，您不能说结果是所有东西上都出现了像小猫一样可爱的东西，但是我们很幸运，这是一个公共地址，因此我们不需要在商店中查找它。 实际上，我们认为不应使其变得如此容易获得。 如果开发人员确实希望确保合同的地址正确，则应使用checkScienceAddress函数，但我们不会感到麻烦。
第二部分：简单假设的崩溃
那么，我们到底想实现什么？ 应当理解，我们没有为自己设定目标，即完全编译字节码，将其转变为人类可读的实体代码。 只要我们知道他的父母是谁，我们就需要一种便宜的方法（无需在战斗区块链中支付交易费用）来确定小猫的基因。 这就是我们要做的。
首先，让我们使用Etherscan
操作码工具进行快速分析。 看起来像这样：
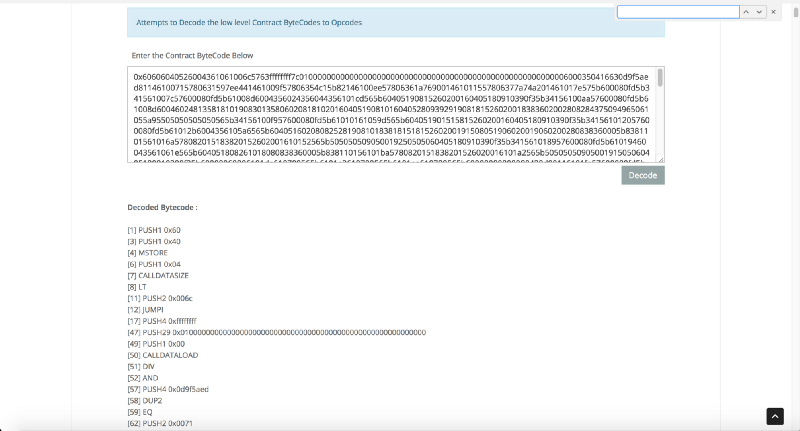更清晰我们遵循解码汇编程序代码的黄金法则：我们从关于程序行为的简单而大胆的假设开始，而不是试图从整体上理解其工作，而是着重于确认所作的假设。 我们将遍历字节码以回答一些问题：
- 它使用时间戳吗？ 否，因为缺少TIMESTAMP操作码。 如果其中有任何简单的事故，那么它的来源肯定是另一个操作码。
- 是否使用块哈希？ 是的，BLOCKHASH发生了两次。 因此，它们的操作码可能会产生随机性，但我们尚不确定。
- 是否使用任何散列？ 是的，有SHA3。 但是，不清楚他在做什么。
- 是否使用msg.sender？ 否，因为缺少CALLER操作码。 因此，没有访问控制应用于合同。
- 是否使用任何外部合同？ 不，没有CALL操作码。
- 是否使用COINBASE？ 不，因此我们排除了另一个可能的随机性来源。
收到这些问题的答案后，我们提出并打算检验一个简单的假设：mixGene的结果由该函数的三个且只有三个输入参数确定。 如果是这样，那么我们可以简单地在本地部署此合同，继续使用我们感兴趣的参数调用此函数，然后，也许甚至在猫妈妈受精之前，我们也可以得到一套小猫基因。
为了验证这一假设，我们在主网络上使用三个随机参数调用mixGene函数：1111115、80、40，并得到一些结果X。接下来，使用
truffle和testrpc部署此字节码。 因此，我们的懒惰导致了使用松露的某种非标准方式。
contract GeneScienceSkeleton { function mixGenes(uint256 genes1, uint256 genes2, uint256 targetBlock) public returns (uint256) {} }
我们从合约框架开始，将其放入松露框架的文件夹结构中，然后执行松露编译。 但是，我们没有将这个空的合同直接迁移到testrpc，而是将构建文件夹中的合同字节码替换为实际的扩展字节码和geneScience合同字节码。 如果您想仅使用字节码和某些有限的开放接口来部署合同以进行本地测试，则这是一种非典型但快速的方法。 之后，我们直接使用参数1111115、80、40调用Mixgenes，不幸的是，响应返回时出现错误。 好吧，再深入一点。 众所周知，mixGene函数的签名为0x0d9f5aed，因此我们用笔和纸来跟踪字节码的执行，从该函数的入口点开始，以考虑堆栈和存储中的更改。 经过几次JUMP之后，我们发现自己在这里：
[497] DUP1 [498] NUMBER [499] DUP14 [500] SWAP1 [501] GT [504] PUSH2 0x01fe [505] JUMPI [507] PUSH1 0x00 [508] DUP1 [509] 'fd'(Unknown Opcode)
从这些行的内容来看，如果当前块的数量小于第三个参数，则调用revert（）。 好吧，这是相当合理的行为：在游戏中调用带有未来编号的实数函数是不可能的，这是合逻辑的。
这种输入验证很容易规避：我们只是在testrpc上挖了几个块，然后再次调用该函数。 这次，函数成功返回Y。
但不幸的是X！= Y
太可惜了 这意味着函数执行的结果不仅取决于输入参数，还取决于主网络的区块链状态，这当然与假区块链testrpc的状态不同。
第三部分：卷起袖子，深入栈中
知道了 因此，是时候卷起袖子了。 纸张不再适合跟踪纸堆状态。 因此，为了进行更认真的工作，我们将启动一个非常有用的EVM反汇编程序
evmdis 。
与纸和笔相比，这是一个切实的进步。 让我们继续上一章的内容。 以下是evmdis令人鼓舞的结论：
............. :label22 # Stack: [@0x70E @0x70E @0x70E 0x0 0x0 0x0 @0x88 @0x85 @0x82 :label3 @0x34] 0x1EB PUSH(0x0) 0x1ED DUP1 0x1EE DUP1 0x1EF DUP1 0x1F0 DUP1 0x1F1 DUP1 0x1F3 DUP13 0x1F9 JUMPI(:label23, NUMBER() > POP()) # Stack: [0x0 0x0 0x0 0x0 0x0 0x0 @0x70E @0x70E @0x70E 0x0 0x0 0x0 @0x88 @0x85 @0x82 :label3 @0x34] 0x1FA PUSH(0x0) 0x1FC DUP1 0x1FD REVERT() :label23 # Stack: [0x0 0x0 0x0 0x0 0x0 0x0 @0x70E @0x70E @0x70E 0x0 0x0 0x0 @0x88 @0x85 @0x82 :label3 @0x34] 0x1FF DUP13 0x200 PUSH(BLOCKHASH(POP())) 0x201 SWAP11 0x202 POP() 0x203 DUP11 0x209 JUMPI(:label25, !!POP()) # Stack: [0x0 0x0 0x0 0x0 0x0 0x0 @0x70E @0x70E @0x70E 0x0 @0x200 0x0 @0x88 @0x85 @0x82 :label3 @0x34] 0x20C DUP13 0x213 PUSH((NUMBER() & ~0xFF) + (POP() & 0xFF)) 0x214 SWAP13 0x215 POP() 0x217 DUP13 0x21E JUMPI(:label24, !!(POP() < NUMBER())) # Stack: [0x0 0x0 0x0 0x0 0x0 0x0 @0x70E @0x70E @0x70E 0x0 @0x200 0x0 @0x213 @0x85 @0x82 :label3 @0x34] 0x222 DUP13 0x223 PUSH(POP() - 0x100) 0x224 SWAP13 0x225 POP() :label24 # Stack: [0x0 0x0 0x0 0x0 0x0 0x0 @0x70E @0x70E @0x70E 0x0 @0x200 0x0 [@0x223 | @0x213] @0x85 @0x82 :label3 @0x34] 0x227 DUP13 0x228 PUSH(BLOCKHASH(POP())) 0x229 SWAP11 0x22A POP() :label25 # Stack: [0x0 0x0 0x0 0x0 0x0 0x0 @0x70E @0x70E @0x70E 0x0 [@0x200 | @0x228] 0x0 [@0x88 | @0x223 | @0x213] @0x85 @0x82 :label3 @0x34] 0x22C DUP11 0x22D DUP16 0x22E DUP16 ...........
evmdis的真正优点是可以将JUMPDEST分析成正确的标签，而这不能被高估。
因此，在通过初始需求之后，我们发现自己位于标签23上。我们看到了DUP13，并从上一章中回想起堆栈上的数字13是我们的第三个参数。 因此，我们试图获取第三个参数的BLOCKHASH。 但是，BLOCKHASH的作用仅限于256个块。 这就是为什么后面要加上JUMPI（这是一个if-construct）的原因。 如果我们将操作码的逻辑翻译成伪代码的语言，我们将得到如下内容：
func blockhash(p) { if (currentBlockNumber - p < 256) return hash(p); return 0; } var bhash = blockhash(thrid); if (bhash == 0) { thirdProjection = (currentBlockNumber & ~0xff) + (thridParam & 0xff); if (thirdProjection > currentBlockNumber) { thirdProjection -= 256; } thirdParam = thirdProjection; bhash = blockhash(thirdProjection); } label 25 and beyond ..... some more stuff related to thirdParam and bhash
一些与thirdParam和bhash有关的东西-与thirdParam和块哈希有关的其他代码
现在，我们相信已经找到了导致我们的结果与主网络中观察到的结果不同的原因。 更重要的是，我们显然设法找到了机会的来源。 即：基于第三参数或第三参数的
预测来计算块哈希。 重要的是要注意，在堆栈中，第三个参数也被此预测的块号替换。
显然，在主网络之外进行本地执行期间，我们没有一个简单的方法来施加与主网络的值匹配的BLOCKHASH返回。 既然如此，由于我们知道所有这三个参数，因此我们可以轻松地监视主网络，并获取第三个参数的块H的哈希值以及预测块的哈希值。
接下来，我们可以将此哈希直接插入到本地测试环境中的字节码中，如果一切按计划进行，我们最终将获得正确的基因集。
但是有一个问题：DUP13和BLOCKHASH在代码中只有2个字节，如果仅用33个字节的PUSH32 0x * hash *替换它们，程序计数器将完全改变，我们将必须修复每个JUMP和JUMPI。 否则，我们将不得不在代码末尾制作JUMP，并替换已部署的代码指令，依此类推。
好吧，既然我们走了这么远，我们会再嗅一闻。 由于我们将32字节的非零哈希值推入if分支，因此条件将始终为true，因此，可以简单地将else部分中写入的所有内容扔掉，以便为我们的32字节哈希值腾出空间。 好吧，总的来说，我们做到了：
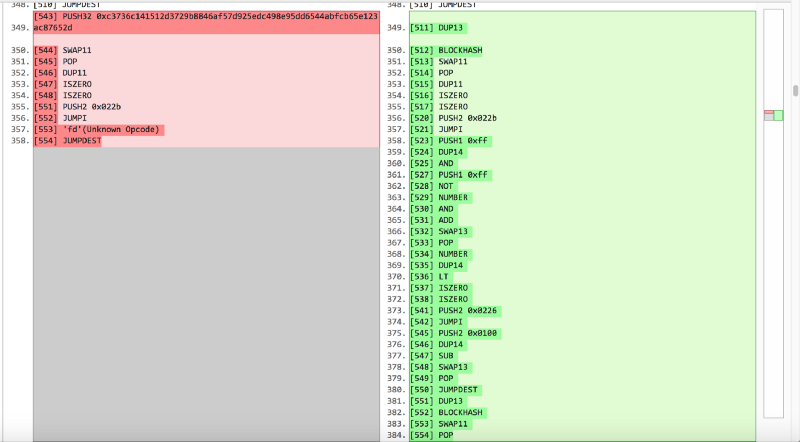
关键点在于，由于我们放弃了条件的其余部分，因此需要在调用之前将mixGene函数的第三个输入参数替换为第三个参数的预测。
这是要点，如果您尝试获取操作结果
mixGene（X，Y，Z），其中currentBlockNumber为Z <256，您只需要将PUSH32哈希替换为Z块的哈希即可。
但是，如果您打算执行以下操作
mixGene（X，Y，Z），其中currentBlockNumber为Z≥256，您将需要用proj_Z块的哈希替换PUSH32哈希，其中proj_Z的定义如下：
proj_Z = (currentBlockNumber & ~0xff) + (Z & 0xff); if (proj_Z > currentBlockNumber) { proj_Z -= 256; } <b> Z proj_Z , mixGene(X, Y, proj_Z).</b>
注意，proj_Z在一定范围的块中将保持不变。 例如，如果Z＆0xff = 128，则proj_Z仅在每个第0个和第128个块上改变。
为了证实这一假设并检查是否有任何陷阱，我们更改了字节码并使用了另一个很酷的实用程序
hevm 。
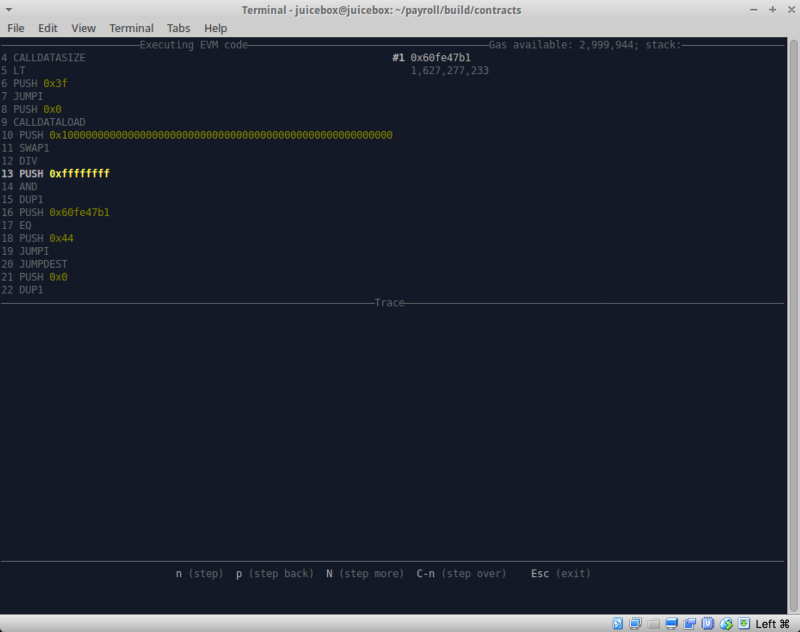
如果您从未使用过hevm，建议您尝试一下。 该工具可以与它自己的框架一起使用，但是最重要的是，它应作为交互式堆栈调试器这样必不可少的工具。
Usage: hevm exec --code TEXT [--calldata TEXT] [--address ADDR] [--caller ADDR] [--origin ADDR] [--coinbase ADDR] [--value W256] [--gas W256] [--number W256] [--timestamp W256] [--gaslimit W256] [--gasprice W256] [--difficulty W256] [--debug] [--state STRING] Available options: -h,--help
以上是启动选项。 该实用程序允许您指定各种参数。 其中包括--debug，它使您能够进行交互式调试。
因此，这里我们多次调用了部署在主网络区块链上的geneScience合同，并记录了结果。 然后，我们使用hevm在考虑到上述规则和...
结果是一样的！
上一章：工作的结论和继续（？）
那么，我们能够实现什么呢？
使用我们的黑客软件，如果刚出生的小猫出生在块的范围内，您可以100％的机会预测其256位基因[coolDownEndBlock（当婴儿准备出现时），当前块为+ 256（大约）]。 您可以对此做出如下推断：当婴儿处于母猫的子宫中时，由于熵的来源会以预测的coolDownEndBlock块的哈希形式出现，因此其基因会随着时间的推移而发生突变，该信息也会随着时间而变化。 因此，您可以使用此程序检查婴儿的基因如果现在出生，将如何显示。 如果您不喜欢该基因，则可以平均再等待256个区块，然后检查新基因。
有人可能会说这还不够，因为即使在母猫怀孕之前，只有100％的预测准确度才被认为是理想的黑客手段。 但是，这是不可能的，因为小猫的基因不仅取决于其父母的基因，而且还取决于作为突变因子的区块预测的哈希值，而这在受精前根本无法得知。
有什么可以改进的地方，这里有什么细微差别？
我们很快检查了智能合约的实际逻辑部分（标签25及其后的所有内容）中堆栈上发生的更改，我们相信mixGene代码的这一可预测部分将得到很好的解析和研究。 我们希望，将区块哈希作为突变因子也具有一定的物理意义，例如，帮助确定应突变的基因。 如果我们设法弄清楚这一点，我们将获得没有突变的原始基因。 这很有用，因为如果您没有良好的源基因，那么即使最好的突变也可能不够。
我们也没有测量256位基因与小猫特征（眼睛颜色，尾巴类型等）之间的相关性，但是我们相信，借助高性能的bot和简单的分类器，这是完全可能的。
通常，我们完全了解CryptoKitties开发团队在短期内稳定突变的意图。 但是这种方法的另一面是能够像我们一样执行分析。
我们还要感谢出色的以太坊社区开发的工具，例如Etherscan，hevm，evmdis，松露，testrpc，myetherwallet和Solidity。 这是一个非常酷的社区，我们很高兴能加入其中。
最后，修改后的代码
https://github.com/modong/GeneScienceCracked/请记住将$ CONSTBLOCKHASH $更改为预测块的哈希。
