合伙制Kaluza-Klein合伙人，第2部分

在上一篇文章中，我解释了为什么对于那些不知道存在附加维度的天真的观察者来说，能够以附加维度运动的粒子具有Kaluza-Klein（KK）伙伴的作用-原始粒子的较重版本。 我指出，当质量为m的初始粒子向附加维度的方向移动时，对于天真的观察者来说，它似乎静止不动且比其应有的重，也就是说，好像它是另一种类型的粒子。 与原始粒子类似但较重的这类所谓的新粒子被称为QC合作伙伴。

对于条带 ，如果质量为m的粒子以p _跨过矩的方式在条带上移动，那么将条带视为直线的观察者将假定该粒子是KK伙伴，其动量和质量为零，其中

$$

$$M ^ 2 = m ^ 2 +（p_ {across} / c）^ 2> m ^ 2$$

尽管通常是这样，但是对于每个大于m的质量M，必须有自己的质量控制伙伴。 但是事实并非如此-我们的世界是量子的（请参阅上一篇文章的图1）。 现在，我们确切地找到了量子力学如何改变整个画面。

我们需要的量子物理学的关键特征是，对于在有限尺寸测量中运动的量子“粒子”，并非所有可能的p _跨度值_都是允许的。 用更笼统的表述：量子力学表明，以有限尺寸进行测量的“粒子”在该方向上只能具有某些动量值。

这是量子力学最重要，最奇怪的结果之一！ 乍看之下，这完全是违反直觉的，因为什么可以阻止您要求动量p的“粒子”略微加速，以使其动量与p略有不同？

什么是量子？

您可能已经注意到，我开始引用“粒子”一词，因为在当前情况下，我们需要从一个直观的概念中区分用于描述电子，介子，夸克，胶子和所有其他已知基本粒子的术语“粒子”。我们从灰尘，沙子，盐和碎石的经验中继承下来的颗粒。 最好将这样的“粒子”称为电子，光子，夸克等，量子，更狡猾的物体。 这些量子是电场的扰动；它们更像是波，而不是粒子。 理解量子的最好方法是想象波。 这是另一个重要的语言学观点：当我说“波浪”时，我的意思不是像海洋中的另一波浪在岸上破碎一样，而是指一系列波峰和波谷。

这样的波的一个例子是电磁波，电磁波也包括我们的眼睛可以分辨的光波。 想象一下，我们采取了这样的波浪-例如，激光-并且我们使光线越来越暗。 怎么能闷闷不乐？ 事实证明，在我们的量子世界中，存在着最微弱的可能的闪光，我们称之为光量子或光子。 光子是光波，其波高和强度是所有可能的最小的。 我们将所有这些概念和名称归功于爱因斯坦，尽管爱因斯坦对量子力学的概念性后果一无所知，但他还是这一理论的奠基人之一。

从我的角度来看，没有直觉可以理解，光波是由量子组成的，因为这在我们直接观察到的任何过程中都没有表现出来。 但是，由于我们不了解的过程，我们的身体不断使用这一事实。 灯光似乎在我们的大脑中持续不断，但是实际上我们的眼睛一次只能吸收一个光子。 此外，我亲眼看到了光由量子组成的确认-我不仅从书本上知道这一点。

我们物理学家通常将这些光量子称为“光粒子”，因为它们在许多方面表现得像粒子。 任何光子本身成直线运动，都具有一定的能量和动量。 所有光子具有相同的质量值（特别是零）； 光子不能分为较小的部分； 光子只能整体发射或吸收。 这些特性大致与我们的直觉期望的颗粒相对应，例如沙粒，玻璃球，灰尘颗粒等。

但是，由于许多原因，“量子”一词比“粒子”一词好，因为量子的某些性质类似于粒子的性质，而某些则类似于波的性质。 波浪行为的一个著名示例是一种量子方法，该方法同时穿过两个门并彼此相互作用（在某种意义上，波浪彼此相互作用，而波谷的波谷相互破坏）。 然后，我们将看到另一个示例。

必须记住，对光子所做的事情也对所有已知的“粒子”所做的事情。 实际上，它们中的每一个都是一种量子-在相应场中具有最低可能高度的波。 电子是电场的量子。 夸克是夸克场的一个量子。 Z粒子是Z场的量子，依此类推。

量子-QC合作伙伴

现在是时候找出我答应向您解释的内容了：为什么量子的波动性质意味着KK伙伴的粒子质量具有原始值，而不是所有可能的值，都是原始“粒子”的大质量m。 著名的物理学家路易斯·德布罗意 （ Louis de Broglie ）遵循爱因斯坦的第一个想法的痕迹，首次明确定义了波，粒子和量子之间的关系意味着，对于量子而言，存在以下关系：
•他的冲动（类似于粒子的性质），
•及其波长（类似于波的性质的属性）[再次，这里用“波”表示波的序列，波长是指波的波峰之间的距离）。

这种依赖关系可以简单表示：动量= h /波长

h是著名的普朗克常数 ，与光速具有相同的自然基本常数。 普朗克在1900年引入了这个常数，试图揭示一种神秘的物理现象。 这是迈向世界量子本质的第一步。 每次您尝试描述量子力学起重要作用的现象时，常数h都会出现。 在许多公式中，您都可以看到ℏ的值，它仅是h除以2π，因为该值通常对于简化公式更方便。


图 1：考虑沿着条带和管道移动的量子

在某些情况下，要解释量子沿着管道运动比发生在前面示例中的带材运动要容易得多。 几乎所有适用于管道的东西都适用于带钢。 因此，我将一起使用它们。

最轻的质量控制合作伙伴

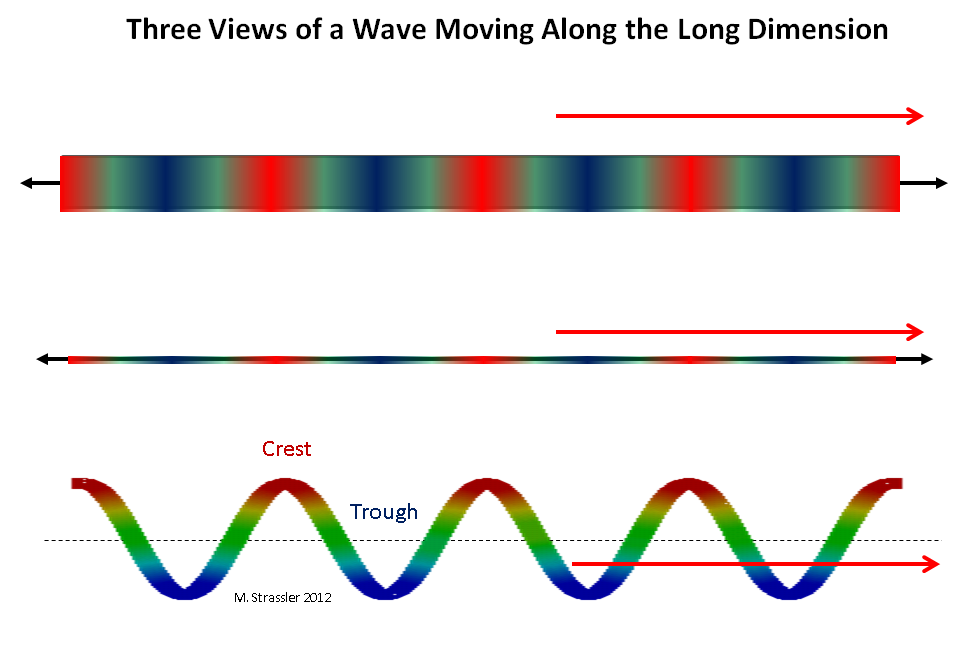图 2：波浪沿长维度的三个视图

想象一个量子沿着宽度为W的条带或沿圆S的管道传播。首先，想象一个沿着长维度移动的量子（长意味着无限大，或者只要我们可以判断它就可以无限长）。 沿着条或管传播的波可以在任何方向上沿长维度移动，并且具有任何波长（两个相邻脊之间的距离）。 见图。 2.根据德布罗意（de Broglie）的说法，这种量子沿着条或管可以具有任何动量：动量可以是零，非常小，很小，很大，在任何方向上等等。 原则上，可以通过沿量子的运动方向（或相反方向）推动量子而使脉冲变大（或变小）。


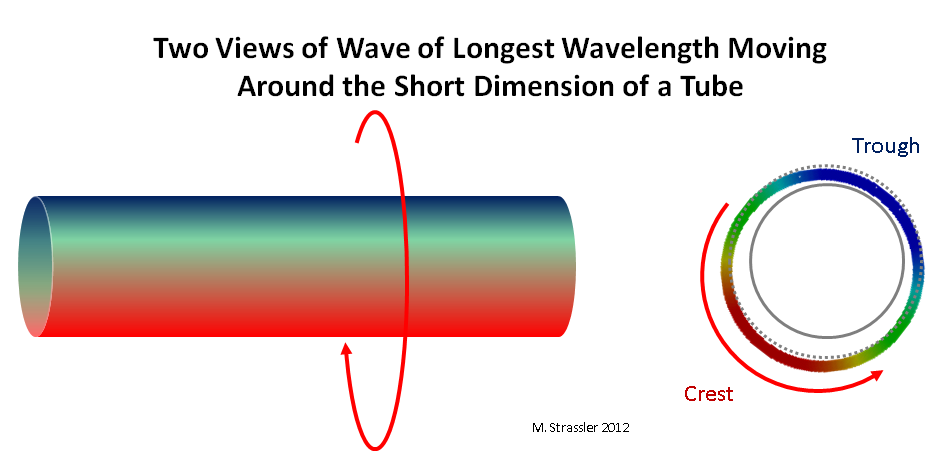图 3：沿着管道的短尺寸移动的波浪的两个视图

现在考虑在条或管上移动的量子（即“粒子”）。 首先，显然它的波长将不能大于条带的横向距离或管子的圆周！ 这在管道上很容易看到：沿着管道安装的至少一个脊（红色）和一个凹陷（蓝色），如图2所示。 3.如果波长大于S，则该波将不会与其自身连接，如图2所示。 4.最长的波长恰好是S； 波浪的唯一空腔应恰好位于管道中与唯一波峰相反的一侧。


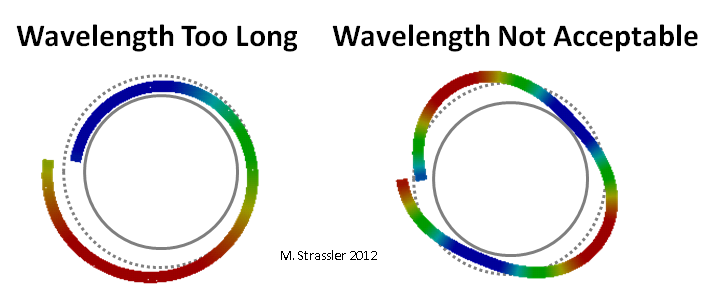图 4：波长不合适

图中波浪的波峰和波谷。 3在管道中移动，类似于（图5）普通的非量子粒子（在这里我的意思是像沙粒，不是量子或“粒子”）沿着管道滚动，但有一个重要区别：如果普通的直观粒子没有问题由于波的动量会略微增加或减少，因此波的运动速度可能会稍快或慢一些，与该波相对应的量子不能具有稍大或较小的动量，因为这将对应于不可接受的波长（图4）。


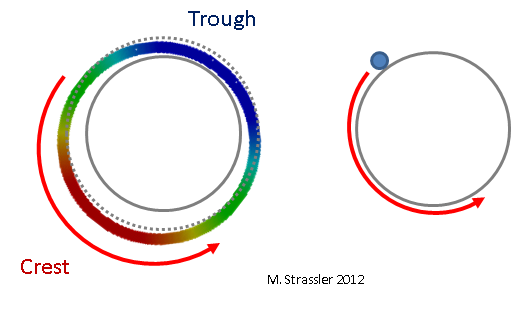图 5：类粒子波

在条带上，这有点棘手，但是如图2所示。 同样，在图6中，在一个壁上只能有一个波峰，而在另一壁上则只有一个波峰，这种情况会随着时间而变化：波峰不移动，但尺寸减小并变成了凹陷，而凹陷变成了波峰。 注意，与图相反。 3，波峰和沟槽保持其大小但沿管道移动时，此波波的波峰不移动而是收缩。 因此，它被称为“驻波”。 对于类似（但不完全相同）的示例，想象一下吉他或小提琴的弦。 直觉上，该驻波对应于普通非量子粒子在条带上前后移动。 （从直观上讲，更精确地讲，它对应于一个同时在两个方向上移动的普通粒子。但是，这个非常奇怪而酷的量子事实现在不重要了。） 7


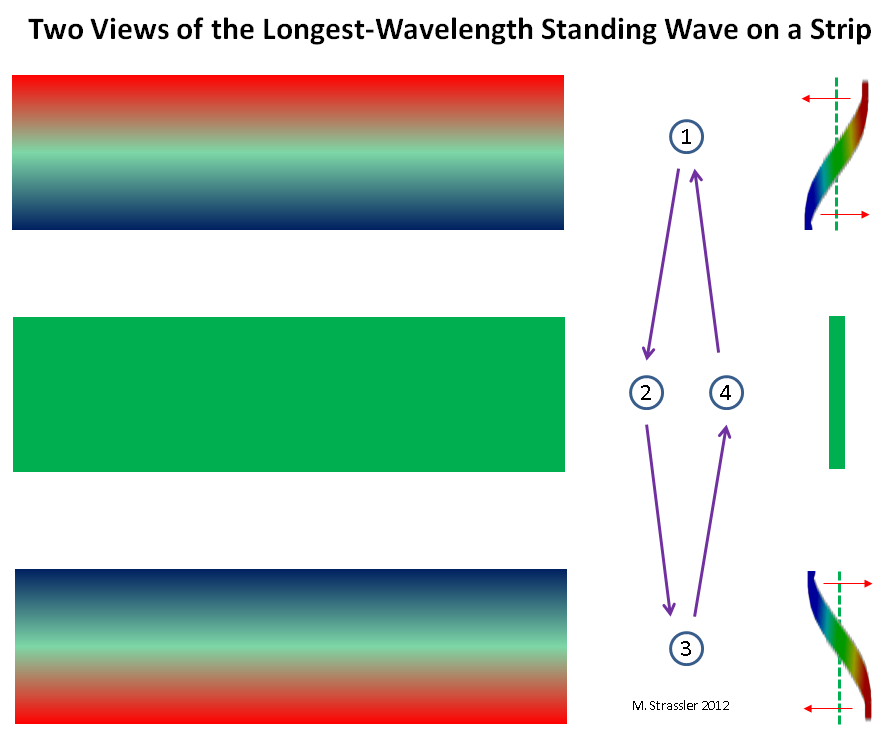图 6：波长最长的驻波的两个视图

在这两种情况下，都有最大可能的波长（对于管道来说，S，对于带材来说是2W）。 这就意味着要有最小的脉冲（管道和带钢的h / S和h / 2 W）。 最后，这意味着有最简单的KK粒子！ 对于质量M，

$$

$$M ^ 2 = m ^ 2 +（p_ {across} / c）^ 2 = m ^ 2 +（h / c S）^ 2 \ quad（pipe）\\ M ^ 2 = m ^ 2 +（p_ { } / c）^ 2 = m ^ 2 +（h / 2 c W）^ 2 \ quad（strip）$$

请注意，对于无质量粒子m = 0，这些公式可简化为：

$$

$$M = h / c S \四边形（管道）\\ M = h / 2 c W \四边形（条形）$$

如果S和W非常小，那么这些最后的公式是正确的，这在合理的推理中通常是这样。


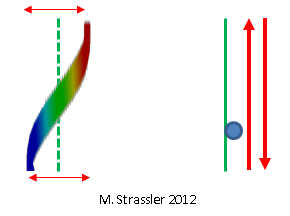图 7：驻波的量子有点像粒子来回运动

因此，我们了解到，由于“粒子”实际上是量子，其性质类似于波的性质：

• 在最轻巧的KK伙伴中，质量M远远大于m，
• 由于M的公式包括1 / W和1 / S，因此附加维数越小，最轻的KK伙伴越难。
• 实际上，当S和W变得如此之小以至于M大大超过m（或者m最初根本为零）时，M大约正比于1 / S或1 /W。

太好了 这是重点，因此在继续之前，请务必先了解它。 还有一件事需要解释：

• 为什么有许多质量不同的M，M'，M”等KK合作伙伴。 （根据定义，其中M <M'<M，等等。）
• 为什么这些质量彼此分离。
• 为什么质量会随着额外尺寸的减少而增长。
• 为什么能够在相同的附加维数上移动的不同类型颗粒的KK伙伴具有相似的质量，尤其是对于较重的KK伙伴。
• 为何质量控制合作伙伴会大量向我们提供有关附加测量的形状，大小和数量的直接信息。

从上面的答案可以很容易地得出。

超越最轻巧的质量控制合作伙伴

图 8：最接近最长波长的波，沿着管道的短尺寸移动

为什么有很多KK合作伙伴？ 仅仅因为条或管上的量子波可以具有许多不同的波长。 在图。 在图8、9和10中，可以看到波的长度是最大波的1/2或1/3，对应于（根据爱因斯坦和德布罗意），相对于最小波具有两倍和三倍脉冲的量子。


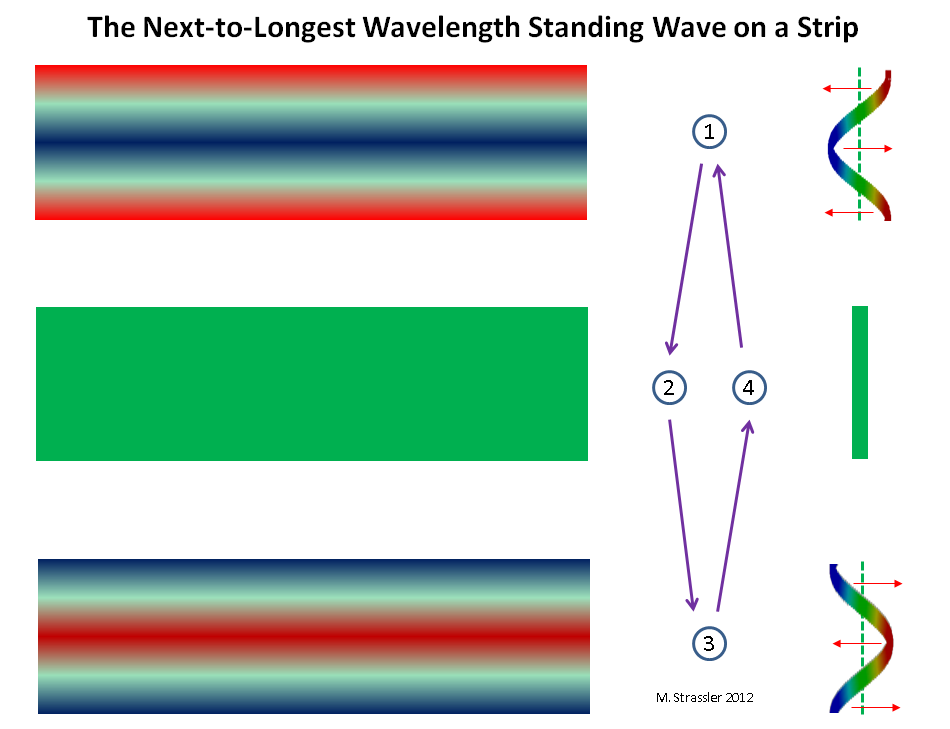图 9条最接近条带上最长波长的驻波

总而言之，我们可以说任何波长都是可允许的，具有n个脊和n个波谷，其中n是任何正整数（1、2、3、4 ..），因此该波长等于S除以n（或用2W除以n），则该波显然适合于圆S的圆内或长度为W的线内。其他任何波长都不适合（请参见图4）。 因此，考虑到德布罗意关系，动量= h / wave_length，允许任何形式为nh / S（或nh / 2 W）的脉冲，并且对于每个n值，我们将有一个KK质量伙伴：

$$

$$M ^ 2 = m ^ 2 +（p_ {across} / c）^ 2 = m ^ 2 +（nh / cS）^ 2 \ quad（pipe）\\ M ^ 2 = m ^ 2 +（p_ { /} c）^ 2 = m ^ 2 +（nh / 2 c W）^ 2 \ quad（strip）$$

这几乎回答了所有提出的问题，至少对于带有管子和钢带的情况而言：

• 质量控制合作伙伴很多（每n> 0个，一个），
• 它们的质量彼此很好地分开（因为当n改变1，M改变非常大），
• 它们的质量随着附加维数的减小而增长（因为当W和S变小时，公式中的最后一项变大），
• 质量不同m的不同粒子的重质KK伙伴具有相似的质量M，因为对于足够大的n，公式中的第二项要比m ^2大 ，这使得KK伙伴的质量大约等于M = nh / c S对于管道和nh带钢为2 c W，几乎与m无关。

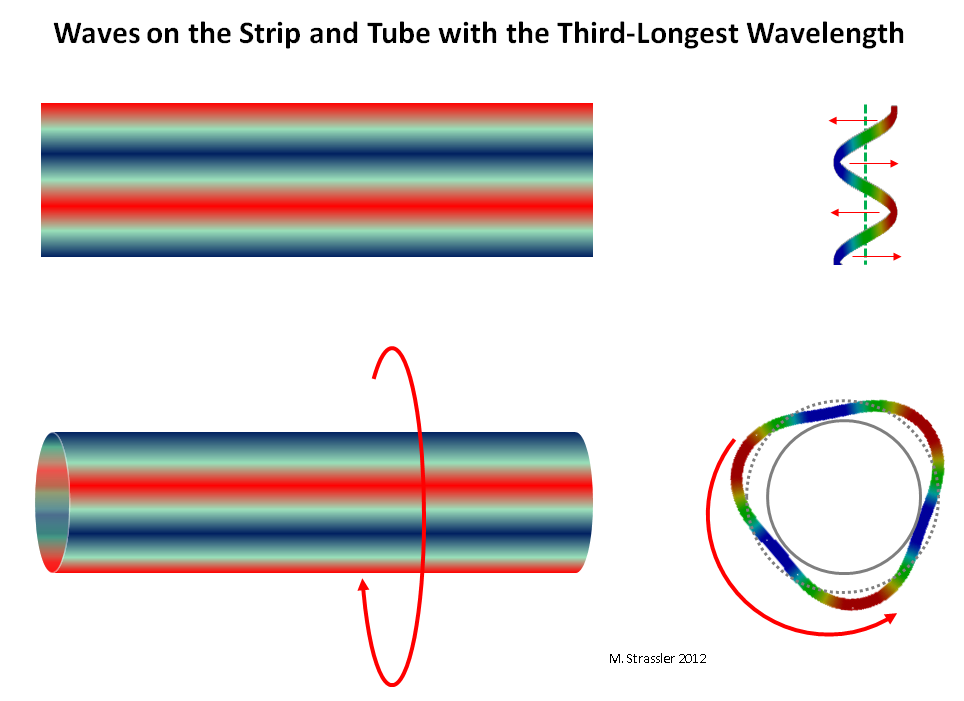图 10：在条带和管道上的波，最大波长为1/3

最后一个问题仍然存在：为什么附加尺寸的数量，大小和形状决定了KK合作伙伴的质量-因此，为什么许多KK合作伙伴的质量测量可以让您确定附加测量的属性，就像聆听乐器的声音就可以基本确定其形状一样，它是由什么尺寸和材料制成的？

举一个极其简化的例子。 我们将再次考虑两个维度，再次使用我们的经典船用通道，包括（如我们在最近的文章结尾处所做的，带有附加测量的示例）以及该通道具有深度的事实，因此我们可以想象其中的波浪（这种波浪可以在大房间里听，或者在水下通过任何频道听）。 通道的横截面（如果在长尺寸线上的任意点处进行切割）将只是宽度为W且深度为D的矩形。就像任何非量子粒子一样，即使从长尺寸的角度来看是固定的，它也可以沿一两个附加方向移动测量（因此在宽度或深度上都有一个脉冲），并且该波在两个附加维度上都将具有波长。 如此简单地将波划分为通过测量宽度进行的操作和通过测量深度进行的操作，尤其将其与通道的矩形联系在一起，通常在其他示例中不起作用。 例如，如图所示。 如图11所示，在顶部，允许的波之一将具有三个用于测量宽度的波谷和一个用于测量深度的波谷。


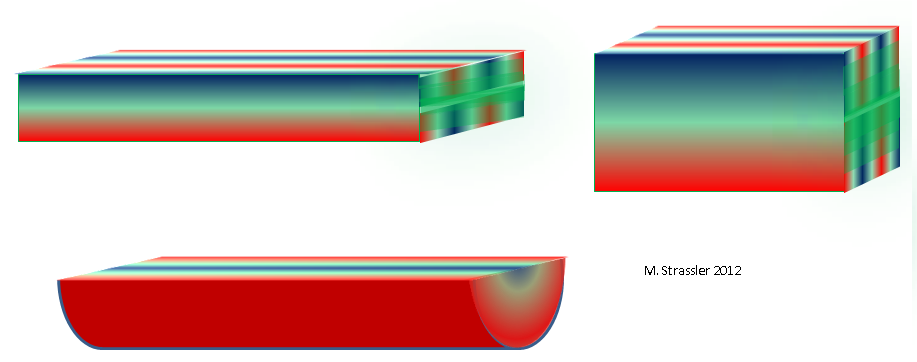图 11

我们可以通过使用整数n ₁测量宽度并测量深度-n ₂来指定凹陷和隆起的数量，对于n ₁和n _2中的每一个（这些值中的一个或两个都可以大于零），我们可以得到KK伙伴。 对于无质量（m = 0）或几乎无质量的量子，KK合作伙伴将具有质量

$$

$$M ^ 2 = m ^ 2 +（p_ {width} / c）^ 2 +（p_ {depth} / c）^ 2 = m ^ 2 +（n_1 h / 2 c W）^ 2 +（n_2 h / 2 c D）^ 2$$

可以看出，质量分布不同于具有一个附加维的情况，并且可以告诉我们W和D。

如果通道的横截面具有不同的形状，例如，三角形或半圆盘形，如图2所示。 在下面的图11中，我们得到了另一个质量分布，该分布反映了三角形或半圆盘的确切形状。 而且我们已经可以丢弃实际的船舶航道并表示三维空间，其横截面对应于任何其他有限的二维形式，图1中显示了其中一种。 关于具有两个空间维度的世界的文章中的 1：完整的磁盘，甚至是球形或圆环。 这些形式中的每一种都将为我们提供自己的质量控制合作伙伴批量销售类型。 如果还有三个，四个或五个额外的维度……也许分布的类型更多。

在图5中给出了无质量粒子的一些分布示例，其中选择了附加测量的大小，以使每种情况下第一个KK伙伴的质量都相同。 12.显然，为了确定其他度量的形状和大小，有必要测量足够数量的KK伙伴的质量（甚至至少要确认新发现的重粒子通常都是KK伙伴），以便了解任何其他度量的性​​质。测量，时间会过去。


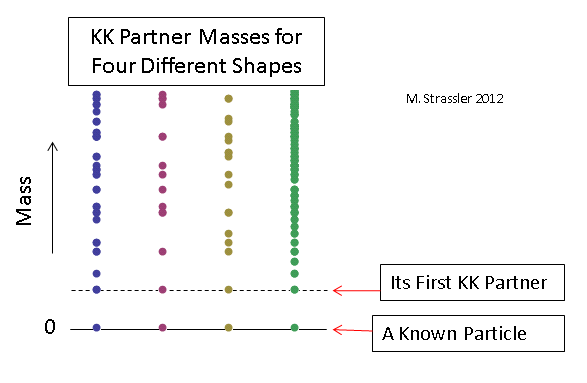图 12

但是，已知的重质物质可以成为轻质物质的KK伙伴吗？

然后出现了明显的其他问题。我们知道，在已知的基本粒子中，有一个电子及其更重的电子：介子和tau。有一个上夸克，它的较重版本是附魔且真实的。有一个较低的夸克，它的重夸克奇特而迷人。重粒子版本是肺部的QC合作伙伴吗？

乍一看，这是一个诱人的假设，但答案是肯定的。不好意思这不是一个愚蠢的问题。它只是一个聪明的否定答案。

Muon和tau，陶醉而真实，奇特而迷人-他们都是因为希格斯场而获得了成功，而不是由于其他维度的冲动。很明显，这是通过详细的实验得出的。可以在文章中找到有关如果希格斯字段为零会发生什么的提示。请注意，如果希格斯场平均为零，则电子，介子和tau不会有质量（并且各自会分解为两种类型的粒子）。这与μ子和tau是电子的KK伙伴的理论不符。

还有许多其他原因。其中最严重的可能是，由于电子上存在电荷，并且由于它被电场包围，因此光子必须在电子移动的任何维度上移动（尽管反之则不成立）。因此，如果电子具有KK伙伴，那么光子也应具有它们。但是从我们的公式（以及与它们类似的更通用的公式）可以得出结论，由于光子没有质量，并且电子质量（0.0005 GeV / c ²）比介子质量（约0.1 GeV / c ^2）小），如果介子是KK伙伴，则光子必须具有类似质量的KK伙伴。但是，如果存在的话，这种粒子将在多年前被发现。实际上，在研究质量远大于Z粒子质量的实验中未观察到光子的KK伴侣-它们的数量为数百GeV / s ²。Z粒子本身也不能成为光子的QC伙伴。她看起来还不够像他。这意味着电子的任何KK配体应至少重。

接下来要去哪里？去实验

我们从理论（其他测量，相关数学和几何的可能性）到预测（QC合作伙伴）。下一步：我们对实验中的其他测量了解多少？我们尚未在实验中见过KK合作伙伴，但我们可能会问，从他们的缺席中我们可以学到什么？正如我稍后将要解释的，还有很多内容，以及在大型强子对撞机和其他地方如何继续寻找额外测量迹象的描述。