在本文中,我将根据量子计算机性能的增长来讨论区块链技术中的安全性问题,讨论一些保护措施以防止使用量子计算机的攻击,以及一个最近的项目:抗量子账本。 根据开发人员的说法,这将是世界上第一个基于后量子加密原理的平台,旨在在这些技术快速发展的情况下提供免受“量子冲击”的保护。 使用经典加密原理构建的平台可能会遭受这样的打击。 如果没有根本性的变化,比特币,以太坊,Ardor和大多数这些平台可能会在不久的将来出现。
第1部分。安全性问题
脆弱性
比特币和类似系统的保护算法基于使用公钥和私钥的非对称加密原理。 使用私钥对交易进行签名,并使用公钥验证其有效性。
使用经典的攻击算法,几乎不可能在知道公钥的情况下找到私钥。 非对称加密系统(例如RSA等)(DSA,DH等)建立在这样的断言之上:分解数的复杂度从密钥的大小呈指数增长。 但是,在量子计算机上使用
肖氏算法 ,有可能在多项式时间内将数字分解为素数,从而在知道公钥的情况下找到私钥。
在2001年,IBM通过将数字15分解为两个主要因子3和5
证明了这一点。为此,使用了由7个量子位组成的量子计算机。 从那时起,量子计算技术的发展一直在加快。
2016年,麻省理工学院的一组研究人员与因斯布鲁克研究所一起,
仅用5个量子位来完成分解数字15的相同任务。
2017年7月,俄裔美国物理学家发明了一台
可编程的51 qubit计算机 。
2017年10月底,来自新加坡和澳大利亚大学的国际研究小组得出结论,区块链中使用的大多数加密协议都容易受到功能强大的量子计算机的攻击。 该
小组的报告对量子计算机的功率增长提供了两种预测:乐观和不乐观。 根据第一,量子计算机的量子位数将每10个月翻一番。 较不乐观的预测表明,每20个月qubit数量将增加一倍。 下图显示了两个预测的图表。
最容易受到量子计算机攻击的是基于椭圆曲线(
ECDSA )创建数字签名的
算法 。 因此,根据
该组织的报告 ,到2027年,经典形式的比特币将被破解。
也许不是一切都那么糟吗? 公钥未以明文形式存储
2017年4月底,bitcoin.com上发表了
一篇文章,以回答比特币持有人是否应该警惕用量子计算机破解它的问题。 它说,尽管在比特币区块链中使用了非对称加密,但用户不必担心他们的硬币的安全性。 公钥未以明文形式存储。 因此,用于转移硬币的地址不是公共密钥,而只是应用SHA-256哈希函数的结果。 哈希函数执行单向转换,因此可以抵抗量子计算机的攻击。
在交易过程中公钥变得众所周知
关于公开密钥显然不可用的说法并不完全正确。 无需赘述,我们将以比特币(BTC)为例分析加密货币如何从一个人转移到另一个人。
让爱丽丝在一个比特币地址的钱包里有100 mBTC(1000 mBTC = 1 BTC)。 她想转让Bob 1 mBTC。 为此,她在她的钱包中指出Bob的比特币地址,转移费和比特币地址,以接收找零。 假设爱丽丝表示1 mBTC作为佣金。 因此,在Alice拥有的100 mBTC中,有1 mBTC发送给Bob,有1 mBTC留给了比特币网络作为佣金,有98 mBTC返回了Alice的钱包。
现在,让我们看看在比特币网络级别会发生什么。 爱丽丝和鲍勃的钱包里有存放硬币的地址。 一个钱包可以包含几个比特币地址。 创建钱包时会生成地址。 每个地址对应于ECDSA算法创建的密钥对:公共和私有。 转移硬币时,会创建一个交易,其中会传输有关爱丽丝传输的硬币数量,鲍勃的比特币地址,爱丽丝的私钥,爱丽丝的
公钥所做的签名以及其他一些数据的信息。 接下来,
以开放(未加密)形式的交易
被发送到网络 。 主机在接受交易进行处理之前,使用公钥验证其签名。 如果签名有效,则将交易信息添加到该区块中。 该切换操作称为确认。
比特币网络中平均区块生成时间为10分钟。 网络试图保持该时间恒定。 在使用收到的资金之前,
建议等待6次确认。 因此,鲍勃在遵守安全规则的情况下,将能够在转移资金大约一小时后使用收到的资金。
在比特币网络上转移硬币的特征之一是不可能仅从一个地址转移一部分硬币。 硬币总是全额转账,位于钱包的比特币地址上,并且零钱会退回给发件人。 既可以从发送硬币的地址获得,也可以从其他任何地址获得。 因此,爱丽丝必须注明送货地址。 在许多操作钱包的软件中,交货地址是发送地址。
严格来说,交易费用不是强制性的,但如果没有交易费用,则可能导致交易延迟很长时间。 反之亦然:您可以通过增加佣金的规模来加快交易速度。 在撰写本文时(2018年1月),大多数钱包软件提供的费用为1 mBTC。 例如,有很多资源,这些资源使您可以根据佣金的大小来估计交易被包含在区块中的时间。
使用公钥1次
从安全的角度来看,最好接收对新地址的更改,而该地址的公钥对于网络来说是未知的。 在这种情况下,密钥对仅使用1次。 但是,根据截至2017年12月的
统计数据 ,约有41.34%的地址被重用。
10分钟进攻
但是,迟早您将需要在新地址使用资金。 公钥以明文方式传输到网络。 在确认未收到之前,资金仍在发送者处。 如果攻击者在交易期间收到公钥,则他将有大约10分钟的时间使用量子计算机获取私钥,并尝试从同一地址进行交易,从而提高了佣金。
静态地址更容易受到攻击
在诸如以太坊,NXT,Ardor等的系统中,公钥在第一次交易后也变得已知。 令牌或智能合约与静态地址相关联的事实使情况更加恶化,因为静态地址可能会受到长期攻击。 如果攻击成功,则攻击者可以根据这些地址破坏整个经济系统。
第2部分。解决方案
如何抵抗量子计算机的攻击?
当前,有几种提供针对量子计算机攻击的保护的基本方法:
- 基于散列的加密;
- 基于代码的密码学;
- 基于矩阵的密码学;
- 基于多维二次系统的密码学;
- 私钥密码术。
这些保护方法具有足够长的密钥并符合安全性要求,能够抵御经典攻击和使用量子计算机的攻击。
研究最多的是基于哈希函数的数字签名的使用。
如前所述,哈希函数执行单向消息转换。 该消息将转换为固定长度的哈希值。 一方面,使用哈希函数应该使搜索消息以获得相似的哈希值变得毫无意义。 另一方面,该算法必须具有抗冲突性:当2条不同的消息对应于哈希函数的相同值时。
Grover的量子算法可用于尝试查找冲突或进行初步攻击以查找原始消息。 这将需要
Ô (2 ˚F ř 一个Ç Ñ 2 ) 操作。 因此,为了维持128位安全性,所得哈希的长度至少为256位。 作为这种功能,可以选择SHA-256。
灯港签名
在数字签名中使用哈希函数的一种选择是Lamport签名。 它可以基于任何单向哈希函数构建。 该算法的密码稳定性基于使用的哈希函数的密码稳定性。
签名方案留言
中号 长
米 密钥已生成。 首先,成对生成私钥
在S K个 长
ñ ,然后使用哈希函数,由私钥形成公钥对
P K个 。 私钥和公钥对的数量等于原始消息中的位数。
签名时,将逐位读取一条消息,然后根据当前位的值选择相应对中的一个私钥。 选定的私钥组合成一个签名。 接下来,生成的签名和
米 成对的公钥被发送给接收者。
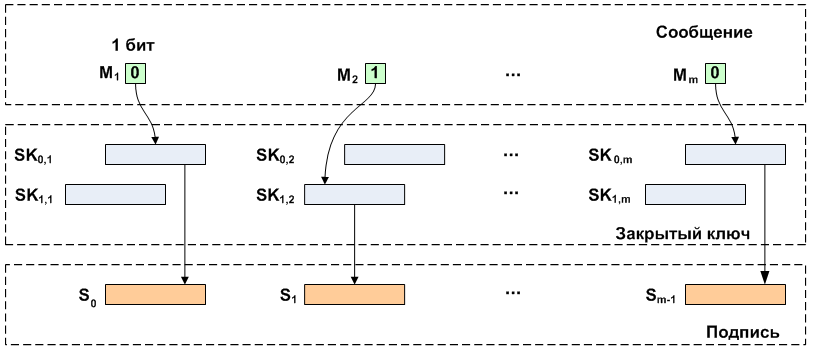
验证签名类似于创建签名的过程。 签名被分成长度不一的片段
ñ 然后使用相同的哈希函数进行转换。 逐位读取消息,并且该位的值选择公钥,将其与接收到的哈希值进行比较。
通常,在应用签名之前,会对原始消息进行哈希处理以减小其大小。 让SHA-256被选择为哈希函数,然后
m=n=256 。 在这种情况下,公钥(以及私钥)的总长度
LPK 结果是相等的:
LPK=n∗2∗m=256∗2∗256=128KB=16KB
签名长度
LS 是:
LS=n∗m=64KB=8KB
Lamport的签名是一次性的(仅当使用一次时才保持安全),因为在执行和传输时,已知一半的私钥。 假设消息长度为256个字节,哈希长度为256个。在Alice发布消息签名之前,没有人知道密钥中的2 * 256个随机数。 因此,没有人可以创建一组正确的256个数字进行签名。
爱丽丝发布签名后,没有人仍然会知道剩余的256个数字,因此将无法为具有不同哈希值的邮件创建签名。
Lamport的签名是一次性的,加上令人印象深刻的签名和公共密钥的总量(24 KB,消息长度为256字节,哈希长度为256字节),这一事实使其在公共事务块中的使用不合适。
温特尼茨签名
还有其他的一次性数字签名算法。 在Vinternytsia的签名中,与Lamport的签名相反,原始消息不是按位签名的,而是成块的。 像Lamport一样,Winternitz的一次性签名可以建立在任何强大的加密功能的基础上。
签名方案留言内容
M 长
m 分成碎片
Mi 长
w 。 每个片段都会生成一个私钥
SK 长度
n 。 对于每个私钥,将依次应用哈希操作
2w−1 次(回合
R ) 作为操作的结果,获得了相应的公钥
PK 相同长度
n 。
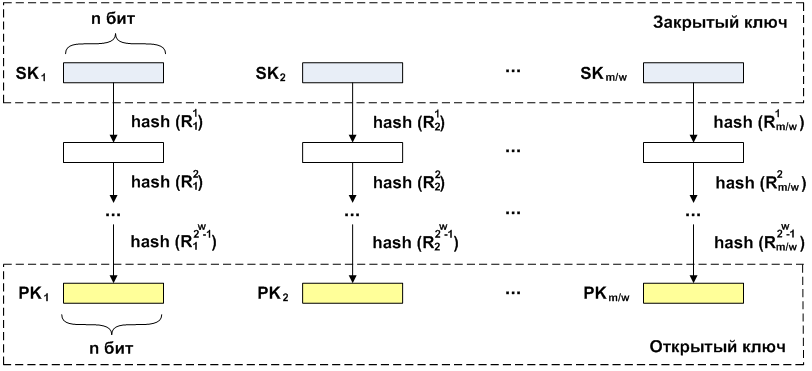
签名时,如生成公共密钥一样,对私有密钥进行哈希的迭代计算。 每种情况下的重复次数取决于所签名的消息。 如前所述,该消息分为多个长度块
w 。 该块的数值
Mi 是为获得签名而必须对私钥执行的迭代次数。 接收到的块的连接将成为该消息的签名。
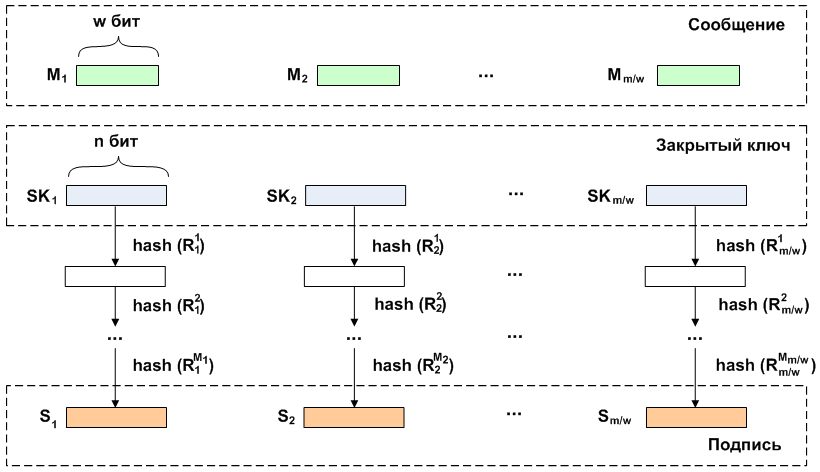
在签名上检查其长度的片段时
n 迭代计算哈希。 轮数
Ri 哈希函数的应用定义为获得公钥的迭代次数与消息块的数值之间的差,即
Ri=2w−1−Mi 次。 然后将获得的值与相应的公钥进行比较。
例子我将通过一个小例子来说明上面的内容。 让消息发出
M (以位表示)长度
m ,参数Vinternitsa
w 和一些哈希函数的长度
n :
M=11000111\:01100111,m=16,\:w=8,\:n=256
产生
m/w=2 基于伪随机数生成器的私钥。 对于每个私钥,我们应用
2w−1=$25 一次哈希函数,从而得到
2 组合成一个长度公用密钥的公共密钥
2∗n=512 一点。 每个消息块的下一个
M 长度
w 确定应用于私钥的哈希操作数
Ri 。 在这种情况下,这些将是值
110001112=19910 和
011001112=10310 相应地。 对私钥执行哈希操作后,我们获得了长度签名
2∗n=512 一点。
要验证签名,请将其分为多个长度
n 。 我们生产每个零件
Ri=2w−1−Mi 哈希运算。 即
255−199=56 和
255−103=$15 次。 如果运算结果得到与公钥匹配的值,则该消息是可靠的。
当使用SHA-256作为签名Winternitz的哈希函数时,
m=n=256 。
让
w=8 一点。 然后是公钥的完整大小
LPK 和签名
LS 等于:
LPK=LS=m/w∗n=256/8∗256=8KB=1KB
在这种情况下,哈希计算操作的数量等于:
P=(2w−1)∗m/w=(28−1)∗256/8=8160
对于
w=16 ,此值增加到
P=1048560 。
公钥和签名的大小(与Lamport签名示例中的参数相同)为1 KB。 总体而言,这比Lamport签名(24 KB)小。 但是,在这种情况下,哈希计算的数量为8160。当然,这是非常多的。 另外,在检查签名时,平均执行此迭代次数的一半。 这使得该签名选项不适用于区块链。
对Winternitz进行签名有多种选择,包括扩展签名以提高可靠性并减少哈希函数的使用次数。 它们的描述超出了本文的范围。 那些感兴趣的人可以
在这里看到更多。 在
这里可以看到基于GOST 34.11-12的家用哈希函数的签名Vinternitsa的应用。
默克尔树(MSS)
一次性签名可以提供令人满意的密码安全性,但是一次性使用签名会成为一个严重的问题。 让我们有必要将储蓄从一个地址转移到另一个地址。 事实证明,使用一次性签名时,有必要每次转移全部资金,并且对于每笔交易,都需要一个新的地址。 对于每笔交易,您将需要发布一个新的公共密钥。 此外,将新交易存储在区块链中将逐渐需要越来越多的时间来搜索它们。
为了解决该问题,他们通过基于每个地址的几个密钥对进行几个签名来扩展签名方案。 几个签名的使用是基于二进制哈希树-Merkle树执行的。
更多细节一棵树的计算是从叶子到根。 树的每个节点叶都根据生成的公钥计算为哈希。 其余节点是通过从子节点的串联(粘合)获得哈希值来计算的。 因此,将整个树计算为根。 假设有4个密钥对,则通过计算7个散列来计算Merkle树(请参见上图)。
Merkle树的一个特征是,可以通过计算根来以密码证明任何节点或叶的存在。
消息签名是使用所选密钥对中的私钥创建的。
签名验证涉及根据传递的参数计算根并将其与可重用的公钥进行比较。 这些参数是:
- 签名
- 根
- 一次性密钥,签名的关闭部分;
- 沿从选定叶到根的路径散布的树哈希。
使用一次性Merkle或Winternitz签名时,无需传输单独选择的一次性公钥,因为它可以从消息签名中获得。 , . , : , , — 0 (
PK1 )
H2 和
H6 。
PK1 , ,
H1 。
H1 和
H2 H5 。
H5 和
H6 R , .
通过公用密钥编译和计算的Merkle树允许而不是发布它们的整个集合而仅发布树的根。通过在签名中包含树的一部分,可以增加签名的大小,但是可以仅使用1个散列来检查许多签名。所以,随着树的深度N可以签名2 N个帖子。在比特币和以太坊中使用了基于椭圆曲线算法的用于密钥的Merkle树,其中有一篇关于Merkle树的优秀文章。超树
基本Merkle方案的主要缺点是可用签名的数量有限,并且必须在计算Merkle树之前生成一次性签名的所有密钥对。密钥生成和签名时间相对于树的高度呈指数增长。使用超级树时,可以延迟新密钥的生成,并增加可用对的数量。更多细节, . 2 : . , . . , (. ).
, , . , , . , .
. . , , .
扩展Merkle树结构(XMSS)
电路的完整描述远远超出了本文的范围;更多详细信息可以在这里找到。我将仅介绍基本概念和特征。与Merkle树一样,XMSS方案允许您扩展一次性签名。在将散列连接到父节点之前使用使用子节点的异或(XOR)的位掩码可以增加对使用的哈希函数的冲突的抵抗力。因此,将SHA-256作为哈希函数与扩展方案结合使用时,带有安全性参数(W-OTS +)的Winternitz可使您将安全性从128位提高到196位。根据lenstra196位防御足以抵御简单的蛮力攻击直到2169年。拥有XMSS方案的所有优点,其主要缺点是密钥生成时间长。当前,还有其他Merkle树扩展方案(GMSS,CMSS),与一次性签名算法结合使用,也可以在可抵抗使用量子计算机攻击的区块链中使用。第3部分。思想的实现
量子可持续区块链项目-QRL
在2016年下半年,P。Waterland博士成立了一个小组,致力于开发一种既能进行经典攻击又能使用量子计算机进行攻击的稳定区块链。根据同年年底开发理论部分的结果,已开发区块链的主要文件“白皮书”(白皮书)已公开发布。该文档目前有多种语言版本,包括俄语。QRL的主要功能
1.签名方案和安全性基于基于XMSS连接结构的Winternitz扩展签名算法(W-OTS +,w = 16,SHA-256)应用签名方案。 这种方法允许生成基于签名的地址,避免了在创建巨型XMSS构造时观察到的冗长的计算延迟。 通过简单的枚举可提供196位保护以及可预测的安全性,以防止受到攻击,直到2169年。
2.共识算法-工作量证明在主网络的第一次迭代中,宣布了一种工作量证明共识算法。
3.浮动佣金与交易链中其他区块相比,更大的交易规模需要为每笔交易付费。 根据Waterland的说法,不需要人为佣金的市场(例如,比特币),这与开放式区块链的理想背道而驰。 每笔交易,如果加上最低付款额,必须与其他任何交易一样有效。 矿工可接受的最低付款额应由市场浮动并确定。 即 节点(矿工)必须竞争性地为他们之间的支付建立下界。 在协议级别将遵守绝对最小值。 因此,矿工将自行决定从内存池订购交易,以将其包含在区块中。
4.动态块奖励计算每个新创建的区块将包括包含采矿地址的第一个币库交易,对此的奖励将定义为币率的奖励金额以及区块内交易的佣金总额。
5.积木花费的时间为1分钟比特币网络中各个区块之间的时间约为10分钟。 有了所需的6个确认,这额外增加了完成交易的等待时间。 较新的交易链区块计划,例如以太坊,在这方面得到了改善,并且由于孤立/过时区块的出现率很高,因此可以在更短的区块时间内受益,而不会失去安全性或集中矿工。
对于QRL,此阻止时间为1分钟。
6.自适应块大小为避免可能出现的纠纷,基于Bitpay提案对现成的自适应解决方案进行了建模,该方案使用乘数来增加块大小
X 中等大小
ÿ 最后
ž 块。 使用平均值不允许矿工进行操作,包括使用空的或溢出的块来更改平均块大小。
X 和
ž 则对于网络必须遵循严格的共识规则。 因此,最大块大小
b 可以简单地计算为:
b = X Y 。
7.货币-量子货币的基本单位是量子。 每个量子被分成最小的元素。 以下是所有元素的名称按升序排列:
| 项 | 价值 |
|---|
| 岸边 | 1个 |
| 中本 | 10 3 |
| 布特林 | 10 6 |
| 默克尔 | 10 10 |
| 兰普波特 | 10 13 |
| 量子 | 10 16 |
因此,涉及部分量子的每笔交易实际上都是大量的肖氏单位。 交易费用以肖氏单位计算并过帐。
8.帐户和地址用户余额存储在帐户中。 每个账户都是一个唯一的,可重复使用的交易链块地址,以“ Q”开头的行表示。
通过在最高XMSS认证树的Merkle根上执行SHA-256创建地址。 此外,还添加了一个四字节的校验和,该校验和由Merkle根的双SHA-256哈希的前四个字节和字母“ Q”组成。
例如,在Python伪代码中,将对此进行如下描述:
Q + sha256(merkle root) + sha256(sha256(merkle root))[: 4]
典型的帐户地址:
Qcea29b1402248d53469e352de662923986f3a94cf0f51522bedd08fb5e64948af479
每个账户都有一个以量子为单位的余额,最多可除以一个肖氏单位。 每笔交易的地址都使用一对新的一次性签名密钥。 从您的帐户发送的每笔交易,称为nonce的交易计数器都会增加。 这允许不存储整个块链的钱包在具有状态保存的超树签名方案中跟踪其位置。
项目的现状和未来的计划
“白皮书”发布后,该小组得到了一些新开发人员的补充,并开始了该计划的实施工作。 定期进度报告已出现在项目网站上。 到2017年4月,QRL区块链测试网络已经启动。 该项目的源代码发布在Github上。 该项目正在Bitcointalk和Reddit上进行积极讨论。
2017年5月,在以太坊生态系统中进行了ICO。 发行了ERC20 QRL令牌。 总共发行了6500万个令牌。 其中有5200万枚代币正在流通中。 在200年的过程中,将逐步发行另外4000万枚硬币。 因此,总发行量将为1.05亿枚硬币。 当主网络启动时,可以将这些令牌以1:1的比例交换为QRL硬币。 当前,可以在交易所(例如Bittrex,Upbit和Liqui)上购买令牌。 下图显示了QRL报价(根据
coinmarketcap.com网站)。
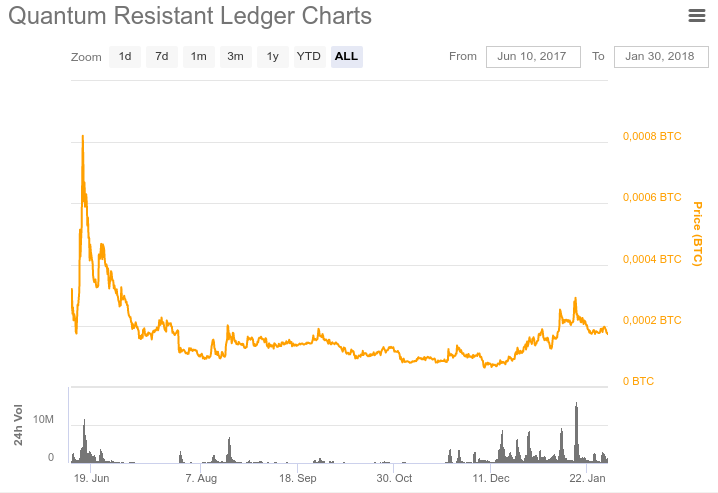
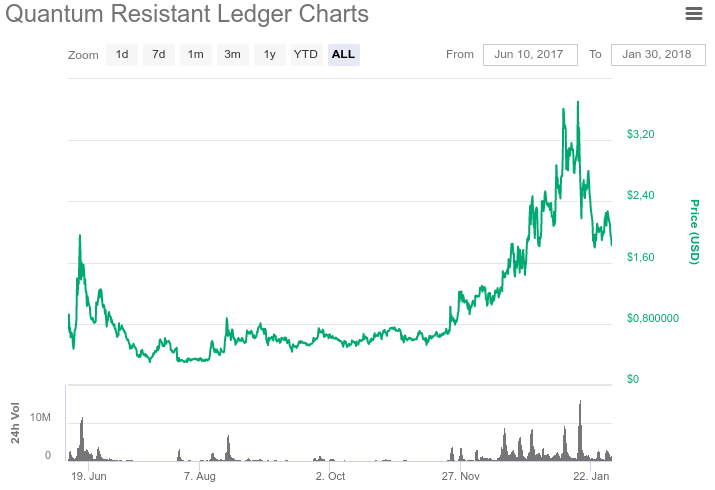
主网络计划于2018年2月至3月启动。
将来,计划将共识算法从工作确认更改为股权确认(权益证明)。 预期的安全停留时间为15-30秒。
结论
量子技术的进步已经启动,不能停止。 随着越来越多的高效量子机器的出现,它们解决的任务范围将不断扩大。 破解现有的不适合量子计算机攻击的加密防御,一直是许多
安全论坛的主题之一。
QRL是第一个旨在解决此问题的区块链技术。 当然,将来还会出现其他人。 他们中哪一个最成功-时间会证明一切。
致谢
作者感谢
kamnik准备了大量的材料,尤其是技术性的部分,以及
SannX的建设性批评和更正。
参考文献
- 肖氏算法 。
- 量子计算机(IBM)上的质因数分解 。
- 在量子计算机(MIT)上将数字15分解为简单因子 。
- 51 qubit计算机的实验报告 。
- 国际研究小组关于量子计算机前面的比特币稳定性的报告 。
- 在比特币区块链中使用ECDSA密钥生成算法 。
- 关于比特币对量子计算机攻击的抵御能力 。
- 比特币网络上的交易确认 。
- 有关比特币网络中佣金的信息 。
- 比特币地址重用统计 。
- 量子Grover算法 。
- 扩展签名温特尼茨 。
- 基于GOST 34.11-12的哈希函数的一次性签名Vinternitsa的应用 。
- 关于以太坊的极客时间 。
- XMSS模式 。
- 伦斯特拉。 密码密钥大小的选择 。
- GMSS
- CMSS 。
- 加密货币系统课程 。
- 年度后量子安全论坛 。
附加材料
- 量子计算机对比特币有害吗?
QRL项目
- 项目现场 。
- 白皮书 。
- 简报
- 博客 。
- GitHub源代码 。
- 关于Bitcointalk的讨论线程 。