
所以你是一个程序员。 为什么甚至需要多项式? 例如,这是一种很好的几何粘土,您可以用它来模制不同的东西。
从我们的
文章以python,血液和炸药为例说明数学分析的本质,可以看出您可以分析和综合任意函数作为多项式。 但是,没有必要专门使用功能。 有时,您可能需要根据多个点或特性(例如曲线的切线)对样条曲线建模。 例如,您需要制作某种动画或漂亮的视频效果,或者绘制一条穿过某些点的曲线,或者创建一个在一个位置平坦而在另一个位置弯曲的曲面。
多项式,甚至包括样条多项式,可能不一定总是执行此任务的最佳工具,但它们具有程序员真正欣赏的某些功能。 它们本质上是简单且通用的,最重要的是,在性能方面非常有效。 以下面的多项式为例:
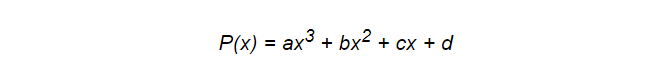
要计算它,只需要6个乘法操作和3个加法。 这很重要,因为您的模型将不断受到计算的影响。 但是在这里我们可以执行优化。 霍纳的计划将帮助我们实现这一目标。 在它的帮助下,相同的多项式可以写为

这只是3个乘法和3个加法。 您知道,我们才刚刚开始,您已经学会摆脱三分之一的计算。
多项式插值
使度数
n的多项式适应空间中
n +1个点的任务称为多项式插值。 有几种方法可以实现它。 您可以使用
牛顿或
拉格朗日插值公式,但是获得插值多项式的最简单方法是求解线性方程组。
如果多项式通过一个点,那么我们显然可以说
P(xi)= yi 。 假设我们要使多项式适应一组三个点。 这意味着:

在一般情况下,我们不能通过三个任意点画一条线。 因此,我们必须弯曲它,形成抛物线。 或者换句话说,引入二阶多项式,也称为二次函数。

由于xs和ys是已知的,因此我们只需要求解该系统并找出系数a,b,c,并且由于该系统由三个方程和三个变量组成,我们通常可以得到一个解决方案。
为确保这一点,请尝试移动下部图表中三个点的位置,然后看看会发生什么。

该图对于线性系统的心理分析也非常有用。 在一般情况下,不可能在三个点上拟合一条直线,就像无法找到具有n-1个未知变量的n个方程组的解一样。 但是有时候有可能。 例如,在某些点重合或所有点有意位于一条直线上的情况下。
相反的情况更加有趣。 我们可以通过两个给定点绘制无数抛物线。 所有这些都同样适合作为该问题的解决方案。 同时,对于n个方程和n +1个变量的系统,我们无法获得一些独特的更好的解决方案。
但是,如果仍然可行怎么办? 如果我们可以引入一些其他准则来选择最合适的选择怎么办?
综合性
类似的问题将我们引向多项式综合领域。 在我们的情况下,这是多项式级数和多项式插值之间的交叉。 使用系列,我们可以在某个时候基于其派生函数建模,使用综合,我们可以同时使用点和派生类(不仅是它们,而且可以同时使用)。
函数的导数与其图的几何特性密切相关。 一阶导数确定切线斜率的切线,而二阶确定曲率。
假设我们需要定义一个通过两个点的函数,同时知道两个点的切线。 在这种情况下,我们可以轻松地将其综合为多项式。
和以前一样,我们需要写下一个方程组。 现在我们需要四个条件,因此我们应该选择一个次数为3的多项式,即三次函数。
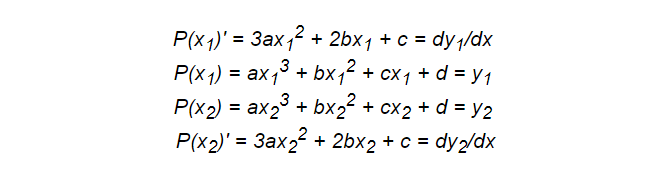
一些方程是基于点的,而另一些是导数的。 还可以在此处添加积分以引入必要的整数属性,这使该技术非常有效。
但是,我们将继续考虑将连续平滑线的两个点与切线约束相连接的函数。


龙格现象
多项式插值法具有令人不快的特性,其表现为该区间两端的振荡增长随点数的增加而增加。 这种现象称为龙格现象。 它限制了使用简单多项式插值的可能性。
这种方法的另一个缺点是它的全局特性,即整个功能的变化以及至少一个点的位置的最小变化。 结合振荡,结果就是混乱。

切比雪夫节点
解决混乱的方法之一是为插补
-Chebyshev节点选择特殊的网格。 这些是特殊的x值,这些值是通过将半径为1的半圆划分为相等的片段并将其投影到x轴上而获得的。
通常,此技术中隐藏了某种数学魔术,但从务实的角度来看,它旨在最大程度地减少龙格现象。 尽管不允许完全预测插值,但一切都在区间(-1:1)上稳定进行。

当然,您可以使用一维仿射变换根据需要扩展X轴上的间隔。 不必遵守段
(-1; 1) 。
但是插值同时保留了它的普遍性。 更改第一个点仍然会影响到最后一个点附近的功能,尽管影响不大。
花键
花键有很多变体,但是它们都被一个应用场景结合在一起。 一旦出于某种原因全局插值不再适合我们的任务,我们就可以将区间分成较小的片段,并为每个片段定义独立的插值函数。
我们唯一需要考虑的是在末端将它们连接以保持连续性。 如果我们不仅保证最终的,逐段定义的函数的连续性,而且还保证其一阶导数的连续性,那么在这种情况下,其每个段的切线将重合,并且其进度表将看起来很平滑。
花键有一定的
分类 。 例如,采用由两个片段组成的多项式样条。 如果它的每个片段都是由三次多项式确定的,则称为三次。 它可能具有例如一阶导数的连续性等性质,因为片段交界处的切线重合。 它的片段宽度不相等。 它不是自然起源的,因为我们可以控制其末尾的导数。 当然,这是一个插值样条曲线,因为它正好穿过我们指示的网格点。

结论
您将不得不实施自己的插值的可能性非常小。 有许多现成的解决方案,在大多数情况下,您只需要选择合适的工具即可完成工作。 这方面的知识并不那么复杂,但是未知单词和名称的数量却可以减少。
本指南的目的是使您对用于多项式和样条的概念有基本的了解。 他绝不会假装是完整的,因为事实上,整本书都写在本材料的每一小章上。 但是,我们至少希望,本材料中的交互式呈现方式不仅对简要介绍有用,而且如果有这种需要,它将有助于您掌握更高级的主题。
