宇宙学-斯坦福。 摘要 讲座1

本文打开了有关斯坦福大学宇宙学的一系列讲义。 可以使用以下语言进行英语讲座： 宇宙学（2013）-伦纳德·苏斯金德-斯坦福大学 。 我观看了视频讲座并愉快地概述了视频。 讲师伦纳德·苏斯金德（Leonard Susskind）讲解非常有趣。 显然，他是一个有才华的人和一个优秀的老师。

斯坦福大学还以我们杰出的同胞安德烈·林德（Andrei Linde）在这里工作而著称，他因对现代宇宙学的贡献而不久将被授予诺贝尔物理学奖。 谁在乎，我建议您观看他的公开演讲“ 宇宙的许多面孔” 。

这是我对自我教育的尝试。 我还是会自己在笔记本上写的。 但是我决定将商务与娱乐相结合。 我希望这对某人也很有趣。

立即做出保留，我试图记笔记与原始文本接近。 但是，在某些地方，我允许我根据自己作为专业物理学家的经验来补充或概括讲师的陈述。 这样做仅仅是为了促进对材料的理解，理解和吸收。

在本文中，第1讲的提要提请您注意，以后可能还会出现续集。

历史回顾

宇宙学是一门非常古老的学科。 宇宙学的历史可以追溯到数千年前。 特别是古希腊人很久以来就对宇宙学有所了解。

这些演讲的时间段不超过二十世纪下半叶，即埃德温·哈勃（Edwin Hubble）发现宇宙膨胀定律的时候。

如果我们谈论宇宙学是一门科学，那么这是一个相当新的知识领域。 现代宇宙学的历史可以追溯到微波遗迹辐射的发现和大爆炸理论的形成 。 而这只发生在1960年代。

到目前为止，宇宙学不是物理学的一个分支，而是属于自然科学的。 也就是说，在宇宙学中，现象学方法占了上风：观察，测量，分类，分类等。

那时，测量精度很低。 因此，不可能制定确切的陈述。 有方程式，但它们是不正确且不准确的。 物理学家一直参与研究过程，因为恒星，星系和其他天体具有诸如角动量之类的物理特征。 由于天体具有化学成分，物理化学家也参与其中。

但是，对于作为一个物理对象的宇宙本身的态度，对于作为一个系统的宇宙，应该使用一组物理原理和相应的精确正确方程式进行数学研究-这是一个相对较年轻的方法。

宇宙的性质

在这些讲座中，宇宙被视为一个物理系统。 我们将使用方程式对其进行研究。 我们可以从一些一般性的观察开始对宇宙的探索。

各向同性

因此，通常来说，可能不是绝对准确的，就像所有物理学都不是绝对准确的一样，第一个观察是宇宙是各向同性的 。

各向同性意味着宇宙在任何方向上看起来都是相同的。 当然，这仅对于足够大的距离才是正确的。 如果您看起来太近，则由于局部不均匀性（例如由于我们的星系形状），可能无法观察到各向同性。

均匀度

如果宇宙是各向同性的，那么可以肯定地说宇宙也必须是同质的 。 同质性并不意味着在各个方向上均一，而是在每个地方均一。 也就是说，无论观察者身在何处，无论是在我们的银河系中还是在其他离我们很远的地方，大范围的宇宙看起来都是一样的。

星系

宇宙尺度上的星系实际上是质量集中点 。 我们可以将它们视为实质要点。 宇宙可见部分的星系总数约为1000亿 $$$10 ^ {11} = 100 \，000 \，000 \，$ 00$ 。 反过来，每个星系也包含大约 $$$10 ^ {11}$ 千亿颗星。 我们必须记住，这是我们可以看到的仅在球体内部的星系数量。 只有天文学家才能用望远镜看到。 就是说，我们能看到的最远距离是整个宇宙存在的距离：光设法到达我们的距离：大约130亿年。

一个有趣的事实。 宇宙可见部分的恒星总数 $$$10 ^ {11} \ cdot 10 ^ {11} = 10 ^ {22}$ ，如果每颗恒星平均有10颗行星，那么事实证明 $$$10 ^ {23}$ -宇宙中阿伏伽德罗行星的数量。 物质的行星痣！ （讲师笑）

反对宇宙同质性的论点。 反驳

考虑一下我们所处的宇宙。 我们肯定知道，因为我们看到宇宙是各向同性的 。 我们假设宇宙也是同质的 。 但是，如果宇宙不是同质的，将会发生什么？

如果宇宙是各向同性的，那么使其不均质的唯一方法就是采用一种壳形式的结构。


异质宇宙的假设。 左边是各向同性的均匀宇宙；右边是各向同性的非均匀宇宙。 中心的十字表示我们。

如果是这样的话，那么在任何其他点上，宇宙都不会是各向同性的。 也就是说，如果我们不想以某种方式相信自己正好位于宇宙的中心，并且整个宇宙在我们周围都具有球对称性，那么我们将不得不承认宇宙不仅是各向同性的，而且是均匀的。

宇宙学原理

因此，如果我们不相信自己正好位于宇宙的中心，那么宇宙必须是同质的。 均匀的宇宙意味着宇宙在整个体积中均匀地填充有粒子（星系）。 这就是所谓的宇宙学原理 。 宇宙学原理是正确的，因为我们的观察结果在某种程度上近似地表明了这一点。

一些天文学家声称他们观察到了宇宙中的大规模异质性。 讲师怀疑这些资料和陈述的可靠性。

当然，关于宇宙同质性的想法并不是绝对准确的。 甚至星系已经存在的事实也表明存在异质性。 顺便说一下，不仅有星系，而且还有星系团。 但是，在相当大的范围内（大约10亿光年），宇宙看起来是均匀的。

起初，宇宙学原理只是一个假设。 但是随着观测数据的积累，人们对它的确认越来越可靠，最后发现了遗物微波辐射，这表明宇宙中物质的初始分布是高度均匀的。

身体问题陈述

有均匀的银河粒子气体。 每个星系都与其他星系相互作用。 整个星系在电气上是中性的。 但是他们在重力上并不是中立的。 它们通过牛顿引力相互作用。 这是大规模的唯一重要力量。 重力作用于星系，并试图将它们拉在一起。

因此，如果您查看宇宙中的任何一点并想知道它应该向何处移动，您可以猜测它从各个侧面被相同数量的质量围绕着。 按照这个逻辑，可以假设星系根本不应该移动，并且宇宙应该是静态的，因为作用在宇宙中任何点上的力的结果为零。 这是绝对错误的！

现在我们得到了宇宙的牛顿运动方程。 您可能会听到，膨胀的宇宙与爱因斯坦的相对论是完全一致的，在广义相对论之前 ，膨胀的宇宙的定律是无法理解的。 这根本不是真的。 也许这在历史上是如此。 但这仅仅是关于日期的历史事实，而不是关于逻辑的事实。 牛顿可以得到一个扩展的宇宙方程。 现在我们将按照牛顿本该做的。

坐标系

在任何物理问题中，首先要做的就是引入坐标系。 与其选择栅格距离作为距离：1米，一百万公里，一千光年，不如选择一个栅格，使它的节点牢固地附着在星系上。 由于宇宙是同质的，所以我们可以做到。 然后，无论宇宙发生什么变化，星系将始终保持在大致相同的坐标上。 也就是说，星系似乎被“冻结”到坐标网格中。

完全不明显可以做到这一点。 如果银河系完全是偶然地并且完全朝着不同的方向移动的，那么我们就无法做到这一点。 但是我们看到星系是偶然移动的。 我们看到星系一致移动，就像它们被嵌入某个坐标网格中一样。 我们所看到的使我们能够做到这一点，因为星系相对于彼此的速度是一致的，并非偶然。

我们介绍一个网格 $$$（x，y，z）$ 。 这些坐标不是以长度为单位测量的。 如果我们考虑两个星系之间有一个间隔 $$$\ Delta x$ 然后距离 $$$D$ 它们之间（以米为单位）表示为

$$

$$D =一个\，\ Delta x$$

在哪里 $$$一$ 是一个比例参数，可以是一个常数，但一般来说可能不是。 标度参数可能与时间有关。 $$$a = a（t）$ 。

因此，根据毕达哥拉斯定理，两个星系之间的距离通常写为

$$

$$D = a（t）\ sqrt {\ Delta x ^ 2 + \ Delta y ^ 2 + \ Delta z ^ 2}$$

当然，参数 $$$一$ 不是一个常数。 如果它是一个常数，那么星系将是静态的，它们将不会在任何地方移动。 这不是我们正在观察的。 我们看到它们飞散了。

哈勃定律

我们写出两个星系之间的相对速度。 我们及时区分了以前的公式。 我们考虑到 $$$\ Delta x$ -这是一个固定的间隔，不能根据构建坐标系的条件进行更改。 然后

$$

$$\ mathcal {V} = \点{a} \，\ Delta x$$

我们在哪里使用符号 $$$\点{a} = da / dt$ 。

现在，我们写出两个星系的相对速度与它们之间距离的比率

$$

$$\ frac {\ mathcal {V}} {D} = \ frac {\点{a}（t）} {a（t）}$$

注意 $$$\ Delta x$ 减小，并且该比率完全不依赖于坐标。 也就是说，该公式对于任何两个星系都有效，无论它们是多远或多近。

这种关系称为哈勃常数参数。

$$

$$H（t）= \ frac {\点{a}（t）} {a（t）}$$

它不依赖于坐标。 然后您就可以用标准格式写

$$

$$\数学{V} = H \，D$$

两个星系的相对速度与它们之间的距离成正比。

您需要了解，如果哈勃没有发现他的法律，我们将永远不会写下来。 另一方面，哈勃定律并不令人惊讶。 有一句话：“最快的马匹领先于所有人，这不足为奇。” 移动得越快，您走得越远。 这是哈勃发现的事实。

宇宙中的物质质量

考虑一些量 $$$\ Delta x \，\ Delta y \，\ Delta z$ 。 我们问一个问题：什么质量集中在这个体积中？ 让 $$$\ nu$ 基本体积中物质的质量 $$$dx \，dy \，dz$ （以千克为单位）。 然后体积 $$$\ Delta x \，\ Delta y \，\ Delta z$ 等于

$$

$$M = \ nu \，\ Delta x \，\ Delta y \，\ Delta z$$

该区域的公制体积是多少？ 由于 $$$D =一个\，\ Delta x$ 我们可以写

$$

$$V = a ^ 3 \，\ Delta x \，\ Delta y \，\ Delta z$$

该区域物质的密度是多少？ 根据定义，密度为 $$$\ rho = M / V$ ，即考虑到前面两个公式，我们得到

$$

$$\ rho = \ frac {\ nu} {a ^ 3}$$

这是物质的标准物理密度。

虽然总质量量 $$$\ Delta x \，\ Delta y \，\ Delta z$ 不会改变，因为星系会被“冻结”到坐标网格中，因此相同体积中物质的绝对密度会发生变化，因为参数 $$$a（吨）$ 取决于时间。

牛顿定理

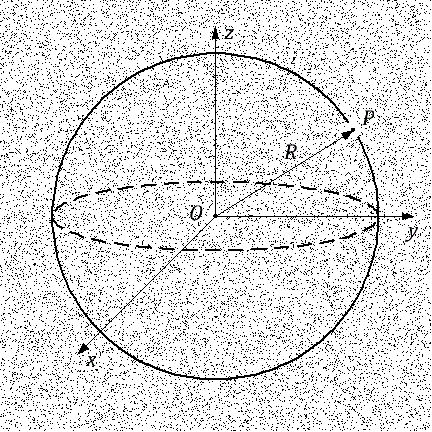牛顿定理的图示

考虑两个半乳。 我们总是可以将其中之一放在原点。 让银河系 $$$O$ 是起源，而银河系 $$$P$ 离她有一段距离。

牛顿定理指出，重力作用于银河系 $$$P$ 仅取决于以原点为中心的球体内的质量 $$$O$ ，并通过银河系 $$$P$ 。 牛顿定理的第二个陈述是，可以认为该球体内的整个质量集中在原点的中心 $$$O$ ，前提是球体内的质量分布不均匀，至少各向同性 。

换句话说，球体内的整个质量对银河系的影响 $$$P$ 相当于该质量集中在一个点上 $$$O$ ，这是球体的中心。

牛顿运动方程

找出星系之间的距离 $$$P$ 和 $$$O$ 。 星系 $$$P$ 有坐标 $$$（x，y，z）$ 即从中心到星系的距离 $$$P$ 等于

$$

$$D = a（t）\ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

我们可以介绍一下符号

$$

$$R = \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

$$$R$ 不是以米为单位，而是以与 $$$x$ ， $$$y$ 和 $$$z$ 并且不依赖于时间。 然后

$$

$$D = a（t）\，R$$

现在，我们记录银河系的速度和加速度 $$$P$

$$

$$\数学{V} = \点{a}（t）\，R$$

$$

$$\ mathcal {A} = \ ddot {a}（t）\，R$$

现在我们必须等同于加速度 $$$\数学{A}$ 半径范围内与整个引力质量相关的加速度 $$$R$ 。 表示星系的质量 $$$P$ 为 $$$m$ 以及球外所有物质的质量 $$$M$ 。 然后，重力作用于银河系 $$$P$ 等于

$$

$$F = -G \ frac {m \，M} {D ^ 2}$$

在哪里 $$$G = 6.67408 \ times10 ^ {-11} \ mathrm {N \ cdot m ^ 2 \ cdot kg ^ {-2}}$ -重力常数。 公式中的减号表示它是一种吸引力。

现在您可以记录星系的加速度 $$$P$

$$

$$\ mathcal {A} = -G \ frac {M} {D ^ 2}$$

我们等于两个表达式 $$$\数学{A}$ 并得到

$$

$$\ ddot {a}（t）\，R = -G \ frac {M} {D ^ 2}$$

我们考虑到 $$$D =一个\，R$ 然后

$$

$$\ ddot {a} \，R =-\ frac {M \，G} {a ^ 2 \，R ^ 2}$$

将两边除以 $$$a \，R$

$$

$$\ frac {\ ddot {a}} {a} =-\ frac {M \，G} {a ^ 3 \，R ^ 3}$$

查找球体的体积

$$

$$V = \ frac {4} {3} \ pi \，D ^ 3 = \ frac {4} {3} \ pi \，a ^ 3 \，R ^ 3$$

我们将右侧的分子和分母乘以 $$$4 \ pi / 3$

$$

$$\ frac {\ ddot {a}} {a} =-\ frac {4} {3} \ pi \，G \，\ rho$$

这个方程式独立于 $$$R$ ，这对于宇宙中的任何星系都是如此。 这个方程是宇宙学的核心基本方程 。

该方程式的后果之一是，如果宇宙不为空，则它不可能是静态的。 从这个等式可以得出，只有当宇宙为空时，它才能是静态的。

鉴于 $$$\ rho = \ nu / a ^ 3$

$$

$$\ frac {\ ddot {a}} {a} =-\ frac {4 \ pi} {3} \ frac {G \，\ nu} {a ^ 3}$$

该方程首先是在亚历山大·弗里德曼（Alexander Friedman）的广义相对论的背景下获得的。 这个方程式不能告诉我们宇宙是在膨胀还是在收缩。 它仅表示比例因子的二阶导数为负。 也就是说，如果宇宙膨胀，那么它会减速，如果宇宙收缩，那么它会加速。

实际上，宇宙正在膨胀，并且没有减速。 我们只是做了牛顿能做的事，所有宇宙学家都一直认为直到1998年左右。 这种模型被普遍接受，并被称为宇宙的标准模型，直到公开发现宇宙的加速扩展。 到目前为止，方程式的右侧只有一个项。 实际上，应该有几个与广义相对论有关的术语。

出发速度

现在写下银河系的全部能量 $$$P$ 作为动力学和潜力的总和

$$

$$E = \ frac {1} {2} m \ mathcal {V} ^ 2-G \ frac {m \，M} {D}$$

能量可以为正或负，具体取决于这两个项之间的比率。 记住粒子的总能量也很重要 $$$P$ 保存。 如果总能量为正，则粒子无法返回。 仅当总能量为负时，粒子才返回。 边界情况是总能量为零。 解方程 $$$E = 0$ 为 $$$\数学{V}$ 查找出发速度。

$$

$$\ frac {1} {2} m \数学{V} ^ 2-G \ frac {m \，M} {D} = 0$$

$$

$$\ mathcal {V} _ {0} = \ frac {2MG} {D}$$

就像银河系一样 $$$P$ 整个宇宙的速度可以高于出发速度，小于出发速度或等于出发速度。 如果宇宙的速度高于离开的速度，那么它就会膨胀并且永远不会开始收缩；如果宇宙的速度低于离开的速度，那么迟早它将开始收缩。

重写总能量方程

$$

$$\ frac {1} {2} m \，\点{a} ^ 2 R ^ 2-\ frac {m \，MG} {aR} = E$$

弗里德曼方程

考虑宇宙速度与离开速度一致的情况。

$$

$$\ frac {1} {2} m \，\点{a} ^ 2 R ^ 2-\ frac {m \，MG} {aR} = 0$$

简化表达式：除以 $$$m$ ，乘以2，除以 $$$a ^ 2 R ^ 2$

$$

$$\ frac {\点{a} ^ 2} {a ^ 2}-\ frac {2MG} {a ^ 3R ^ 3} = 0$$

在第二项中，我们将分子和分母乘以 $$$4 \ pi / 3$ 。 然后在分母中得到球体的公制体积 $$$V$ 。 鉴于 $$$M / V = \ rho$ 我们得到

$$

$$\左（\ frac {\ dot {a}} {a} \ right）^ 2 = \ frac {8 \ pi} {3} G \ rho$$

这称为弗里德曼方程 。 它等效于上面获得的牛顿方程。 因为我们假定总能量为零，所以这样的宇宙会扩展，渐近地减慢到零，但永远不会越过零并且不会开始缩小。

现在回想一下 $$$\ rho = \ nu / a ^ 3$ 。 重写弗里德曼方程

$$

$$\左（\ frac {\ dot {a}} {a} \ right）^ 2 = \ frac {8 \ pi} {3} \ frac {\ nu G} {a ^ 3}$$

参量 $$$\ nu$ 非常灵活。这完全取决于我们对网格的选择。一般来说，我们甚至可以选择它，以便$$$\frac{8\pi}{3}\nu G = 1$ 。 然后

$$

$$\left(\frac{\dot{a}}{a}\right)^2 = \frac{1}{a^3}$$

该方程式的右侧始终为正，因此扩展率
$$˙ 一个永远不会为0。现在回想一下$\dot{a}$$$˙ 一 /一个=H ^-是一个恒定参数哈勃。从方程式还可以看出，Hubble参数从不改变符号。但是，它仍在放缓。哈勃参数随着时间变得越来越少。这个方程对所有宇宙学都极为重要。一种简单的解决方法是寻找某种类型的解决方案，即我们将以以下形式寻找解决方案$\dot{a}/a = H$

$$

$$a(t) = c\,t^p$$

在哪里 $$$c$ 和 $$p是一些常数。$p$

$$

$$\dot{a} = c\,p\,t^{p-1}$$

$$

$$\frac{\dot{a}^2}{a^2} = \frac{p^2}{t^2}$$

$$

$$\frac{p^2}{t^2} = \frac{1}{c^3\,t^{3p}}$$

$$

$$3p = 2\\ p^2 = \frac{1}{c^3}$$

$$

$$p = \frac{2}{3}\\ c = \left(\frac{3}{2}\right)^{\frac{2}{3}}$$

我们已经获得了弗里德曼方程的解。


弗里德曼方程的解图

真正的宇宙只在某个特定时间点遵循此决定，然后开始加速。 牛顿可以做到这一点。 他离得很近。 问了所有正确的问题。 讲师相信牛顿很可能做到了这一点，并收到了这一决定。 但是，有关宇宙的这种信息与他的宗教观点背道而驰，因此他没有发表自己的发现。