引言

本简短说明将讨论Jetlag在我们上一次出现的 4k int 出现中如何构造大气光散射的模型，该模型的缔约方版本在今年4月的2018年修订版演示会上的4k intro组件中名列第12位 。

您可以在此处免费下载没有SMS的二进制文件。

但是，如果您没有Windows，或者您没有功能强大的现代视频卡，那么您将得到一个令人欣慰的傻瓜：

这项工作的音乐是由keen用4klang编写的。 所有的代码和视觉效果都留在我身后。

在这里，我们仅讨论光散射的模型。 其他事物，例如工具，城市模型，照明和材料模型均不受影响。 我可以派出勇敢的人来阅读源代码 ，或者观看我沉迷了几个小时的录音 -大多数开发工作都是通过视频进行的。

想念一个无聊的故事

这项工作的开始是意识到主要的全职工作不会留出时间来完成一份完整的4k工作-它已经快要到三月中旬了，离Revizen还剩几周。
剩下的只是想出一些简单的方法来快速填充几个晚上的compo填充器。 进行另一个愚蠢的重新行进是不尊重观看者，所以我记得几年前我不得不做一个带有散射的着色器，它非常简单，紧凑，同时允许漂亮，尽管相当慢。

在简短的讨论过程中，我坚持自己的观点，我们决定集中精力于以下方面：使风景充满散射光，日落，云层和微弱的光线（翻译为TIL，意为“神射线”。） 为了不将大气层中的台阶数提高到完全非交互式的值，您必须剧烈摇晃（例如蒙特卡洛庭院方法），这会产生可见的噪声。 但是，如果您移动相机并缓慢地改变场景并启动环境轨道并不重要，则可以轻松地混合相邻的帧并暂时消除这种噪点。

Keen很快就写了音乐-在Revision发行前两周就准备好了。 但是，我因流感而严重受伤-患有救护车和传染病-因此，直到我或多或少以某种方式生活到飞往法兰克福的那一刻，我才真正开始从事着色器工作。 这个散射模型的原型已经写在空中。

在截止日期之前剩下的几个小时内（可能是几个之后； D），我们在派对上从沙子和唾液中抽出了派对版本的内部信息，而与此同时我正远离流感，睡眠不足，长时间飞行，以及他经常参加Shader摊牌 现场编码 比赛而 分心 。

大屏幕上显示的版本包含许多文物，并且仅基于具有随机高度的Voronoi图绘制了城市的基本几何形状。

总的来说，第十二名是相当慷慨的。

如上所示，最终版本是在以后以更轻松的方式制作的，一个月每周工作1-2点。 总共花了大约40至50个小时的工作时间。

散射模型

（注意：我不是专业从事图形编程的人。这对我来说是个小小的舒适爱好，如果一百或一百个人在 啤酒 每年的酒时间。 因此，下面描述某些事物和/或错误命名的可能性不为零。 叔叔，打！）

散射模型是从Egor Yusov的文章“使用对极采样进行高性能户外光散射”中借用的，该文章发表在GPU Pro 5书中，具有完全弹出的对极采样。

物理模型

太阳光子轰击地球的大气层并与空气微粒相互作用。 光子可以被粒子散射，这需要改变光子的方向，或者可以被吸收，这意味着光子丢失了，其能量已经转换为其他形式。
这两个过程都是概率性的，并且尤其取决于粒子密度和光子能量（对应于其颜色）。

在手指上，“红色”光子与空气相互作用的机会较小，因此它们可以相对完整地克服大气层的厚度。
然而，蓝色的具有较高的散射概率，这就是为什么它们可以反复改变方向并在到达（或不到达）观察者之前在大气中传播相当长的距离的原因。

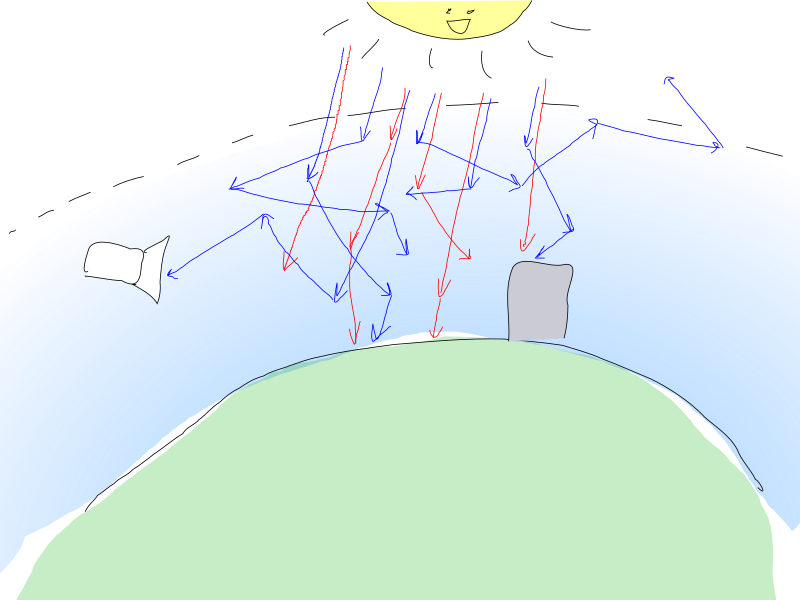
我们感兴趣的光与空气相互作用的参数如下：

• $$$\ beta ^ s（x）$ -点上每单位长度的散射光的分数 $$$x$
• $$$\ beta ^ a（x）$ -某一点每单位长度吸收的光的分数 $$$x$
• $$$\ beta ^ e（x）= \ beta ^ s（x）+ \ beta ^ a（x）$ -某一点每单位长度的总损耗光量 $$$x$
• $$$p（\ alpha）$ 是散射光的角度分布，其中 $$$\ alpha$ 这是入射光束和散射光束之间的角度

假定空气由两种类型的颗粒组成，它们的散射是独立发生的：分子（瑞利模型）和气溶胶（相对较大的球形颗粒，英语文献中为Mie散射 ）。 对于上述参数，型号仅在不同值上有所不同。

对于这两种模型，可以认为相应粒子的密度随高度呈指数下降： $$$\ rho = \ rho_0e ^ {-\ frac {h} {H}}$ 在哪里 $$$\ rho_0$ -海平面上的密度。 赔率 $$$\ beta$ 成比例的 $$$\ rho$ ，其以下含义是针对海平面给出的。

瑞利模型

• $$$p_R（\ alpha）= \ frac {3} {16 \ pi}（1+ \ cos ^ 2（\ alpha））$ [Nishita等。 93，Preetham等。 99]
• $$$\ beta_R ^ a = 0$
• $$$\ mathbf {\ beta_R ^ e} = \ mathbf {\ beta_R ^ s} =（5.8，13.5，33.1）_ {rgb} 10 ^ {-6} m ^ {-1}$ [Riley等。 04，Bruneton and Neyret 08]
• $$$H_R = 7994m$ [Nishita等。 93]

气溶胶

• $$$p_M（\ alpha）= \ frac {1} {4 \ pi} \ frac {3（1-g ^ 2）} {2（2 + g ^ 2）} \ frac {1+ \ cos ^ 2（\ alpha）} {（1 + g ^ 2-2g \ cos（\ alpha））^ \ frac {3} {2}}$ [Nisita等。 93，Riley等。 04]在哪里 $$$g = 0.76$ [布伦顿和内雷特08]
• $$$\ beta_M ^ s = 2 \ cdot10 ^ {-5} m ^ {-1}$ [布伦顿和内雷特08]
• $$$\ beta_M ^ e = 1.1 \ beta_M ^ s$
• $$$H_M = 1200m$ [Nishita等。 93]

单次散射近似

散射近似基于相机每个像素发出的光束以及计算从该方向应该从大气中获取多少光。 每条射线对应于所有三个RGB光分量，就像三个具有相应能量的光子沿着该射线飞行一样。

到达腔室的光是通过空气中的以下过程形成的：

• 散射 （无花果的TIL学习如何翻译散射内）。 添加了太阳发出的光，该光可能以与相机方向对应的角度散射。
• 吸收 。 已经沿光束飞行的光被空气吸收。
• 散射 。 已经沿光束飞行的光会丢失，并向其他方向散射。

出于性能原因，我们认为光只能从一次散射进入相机的方向，而所有其他光（多次散射）可以忽略不计。 不建议在暮光之城使用，但要怎么做。

下图显示了这种方法（我尝试过！）：

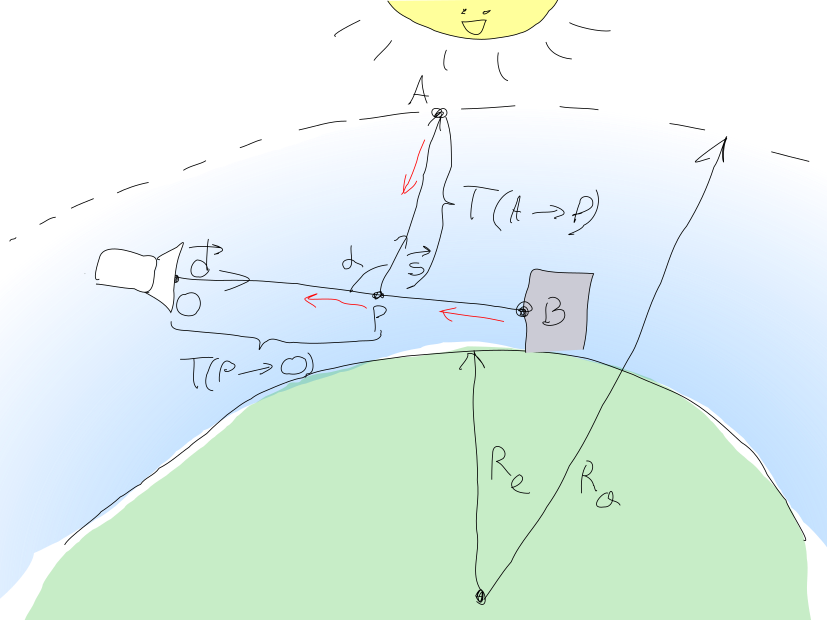
因此，相机像素必须检测到的光量 $$$O$ 可以计算为总和 $$$\ mathbf {L} = \ mathbf {L_ {in}} + \ mathbf {L_ {BO}}$ 在哪里 $$$\ mathbf {L_ {in}}$ -来自太阳的散射光，以及 $$$\ mathbf {L_ {BO}}$ -从该点发出的光量 $$$B$ 对象几何场景到达 $$$O$ 。

灯光几何

$$$\ mathbf {L_ {BO}} = \ mathbf {L_O} e ^ {-\ mathbf {T}（B \ rightarrow O）}$ 在哪里 $$$\ mathbf {L_O}$ 是从某个点发出的光 $$$B$ 对着镜头。

$$$\ mathbf {T}（B \ rightarrow O）$ 点之间的介质的光学厚度 $$$B$ 和 $$$O$ ，其计算方式如下：

$$

$$\ mathbf {T}（B \ rightarrow O）= \ int_B ^ O（\ beta_M ^ e（s）+ \ mathbf {\ beta_R ^ e}（s））ds$$

而成员 $$$\ beta$ 由恒定的海平面和可变的密度组成，此表达式可以转换为：

$$

$$\ mathbf {T}（B \ rightarrow O）= \ beta_M ^ e \ cdot \ int_B ^ O \ rho_M（s）ds + \ mathbf {\ beta_R ^ e} \ int_B ^ O \ rho_R（s）ds = \ bar {\ mathbf {\ beta}} \ cdot \ bar {T_ \ rho}（B \ rightarrow O）$$

请注意，我没有具体透露 $$$\ rho$ ，因为我们稍后会在添加云时对其进行更改。 我还提请注意以下事实： $$$\ beta$ -RGB向量（至少 $$$\ mathbf {\ beta_R}$ 对于RGB组件具有不同的含义，并且 $$$\ beta_M$ -仅为保持一致性而使用的矢量）。 成员与 $$$\ rho$ 在积分下是标量。

阳光

阳光 $$$\ mathbf {L_ {in}}$ 通过积分计算得出 $$$P$ 沿线段 $$$Ob$ 以及所有入射阳光向相机散射并在厚度上逐渐消失的累积 $$$\ mathbf {T}（P \ rightarrow O）$ 。

日照量 $$$P$ 用类似的公式计算 $$$\ mathbf {L_P} = \ mathbf {L_ {sun}} e ^ {-T（A \ rightarrow P）}$ 在哪里 $$$\ mathbf {L_ {sun}}$ -太阳的亮度，以及 $$是从该点发出光线的点 $$$P$ 朝着太阳 $$$\ vec {s}$ 离开气氛。 朝相机散射的光的一部分是 $$$\ mathbf {L_P} \ cdot（\ mathbf {\ beta_R ^ s}（s）p_R（\ alpha）+ \ beta_M ^ s（s）p_M（\ alpha））$ 。

总计，我们得到：

$$

$$\ mathbf {L_ {in}} = \ int_B ^ O \ mathbf {L_P}（s）\ cdot（\ beta_M ^ s（s）p_M（\ alpha）+ \ mathbf {\ beta_R ^ s}（s）p_R （\ alpha））\ cdot e ^ {-\ mathbf {T}（P（s）\ rightarrow O）} ds$$

您可能会注意到：

• $$$\ alpha$ 是相机的每个像素射线的常数（我们认为太阳无限远，并且来自太阳的光线是平行的）
• 赔率 $$$\ beta$ 由海平面常数和密度函数组成 $$$\ rho（s）$
• 功能介绍 $$$p（\ alpha）$ 两种散射过程都有共同的因素

这使您可以将表达式转换为：

$$

$$\ mathbf {L_ {in}} = \ mathbf {L_ {sun}}（1+ \ cos ^ 2（\ alpha））（\ frac {\ frac {1} {4 \ pi} \ frac {3（1 -g ^ 2）} {2（2 + g ^ 2）}} {（1 + g ^ 2-2g \ cos（\ alpha））^ \ frac {3} {2}} \ beta_M ^ s \ cdot \ mathbf {I_M} + \ frac {3} {16 \ pi} \ mathbf {\ beta_R ^ s} \ cdot \ mathbf {I_R}）$$

在哪里

$$

$$\ mathbf {I_M} = \ int_B ^ O \ rho_M（s）e ^ {-\ mathbf {T}（A \ rightarrow P（s））-\ mathbf {T}（P（s）\ rightarrow O）} ds$$

$$

$$\ mathbf {I_R} = \ int_B ^ O \ rho_R（s）e ^ {-\ mathbf {T}（A \ rightarrow P（s））-\ mathbf {T}（P（s）\ rightarrow O）} ds$$

$$$I_m$ 和 $$$I_R$ 仅密度函数不同；它们的指数相同。

没有人能够解析地计算这些积分，因此必须使用重新映射以数值方式进行计算（正如他们在原始出版物中所说的那样，您做不到！）。

数值积分

出于大小和懒惰的原因，我们将其视为尽可能愚蠢的： $$$\ int_A ^ B f（x）dx \大约\ frac {\左| B-A \右|} {N} \ sum_ {i = 0} ^ N f（A + i \ cdot \ frac {\ vec { B-A}} {N}）$

光线行进将在与光流相反的方向上执行：从相机点开始 $$$O$ 在光束与几何形状相交之前 $$$B$ 。 线段 $$$O \ rightarrow B$ 除以 $$$N$ 步骤。

开始进行之前，请初始化变量：

• vec2 （两个独立的分量，用于瑞利散射和气溶胶散射）总累积光学厚度 $$$\ mathbf {T_ \ rho}（P（s）\ rightarrow O）$
• vec3 （RGB） $$$\ mathbf {I_M}$ ， $$$\ mathbf {I_R}$

接下来要说的 $$$P_i$ 之间的每一步 $$$O$ 和 $$$B$ ：

1. 我们来吧 $$$\ vec {s}$ 在太阳的方向，并得到一个点 $$$A_i$ 射线从大气中的出口。
2. 计算厚度 $$$\ mathbf {T}（A \ rightarrow P_i）$ 通过首先计算 $$$\ int_A ^ {P_i} \ rho_M（s）ds$ 和 $$$\ int_A ^ {P_i} \ rho_R（s）ds$ 使用相同的重新行进（步骤数为M ），然后将结果项与相应的常数相乘 $$$\ beta_M ^ e$ 和 $$$\ mathbf {\ beta_R ^ e}$ 。
3. 计算厚度 $$$\ mathbf {T_ \ rho}（P_i \ rightarrow O）= \ mathbf {T_ \ rho}（P_ {i-1} \ rightarrow O）+ \ rho_i（s）\ cdot ds$
4. 积累 $$$\ mathbf {I_R}$ 和 $$$\ mathbf {I_M}$ 使用这些值

重新拼合后的最终颜色由以下各项之和计算得出：

1. 学期 $$$\ mathbf {L_ {BO}}$ 琐碎：包含 $$$\ mathbf {T_ \ rho}（P_i \ rightarrow O）$ 包含价值 $$$\ mathbf {T_ \ rho}（B \ rightarrow O）$ 从 $$$P_i$ 已经达到 $$$B$ 。
2. 通过乘法 $$$\ mathbf {I_R}$ 和 $$$\ mathbf {I_M}$ 到相应的常数并通过相加得出结果 $$$\ mathbf {L_ {in}}$

着色器

没有任何人的简单散射

稍微梳理并注释掉（几乎）直接从内部本身获取的散射源：

 const float R0 = 6360e3; //    const float Ra = 6380e3; //     const vec3 bR = vec3(58e-7, 135e-7, 331e-7); //    const vec3 bMs = vec3(2e-5); //    const vec3 bMe = bMs * 1.1; const float I = 10.; //   const vec3 C = vec3(0., -R0, 0.); //   ,  (0, 0, 0)    //   //  vec2(rho_rayleigh, rho_mie) vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); //    return vec2(exp(-h/8e3), exp(-h/12e2)); } //    ,        float escape(vec3 p, vec3 d, float R) { vec3 v = p - C; float b = dot(v, d); float det = b * b - dot(v, v) + R*R; if (det < 0.) return -1.; det = sqrt(det); float t1 = -b - det, t2 = -b + det; return (t1 >= 0.) ? t1 : t2; } //         `L`   `p`   `d` //   `steps`  //  vec2(depth_int_rayleigh, depth_int_mie) vec2 scatterDepthInt(vec3 o, vec3 d, float L, float steps) { vec2 depthRMs = vec2(0.); L /= steps; d *= L; for (float i = 0.; i < steps; ++i) depthRMs += densitiesRM(o + d * i); return depthRMs * L; } //   (  --   ) vec2 totalDepthRM; vec3 I_R, I_M; //    vec3 sundir; //    ,    `-d`   `L`   `o`   `d`. // `steps` --    void scatterIn(vec3 o, vec3 d, float L, float steps) { L /= steps; d *= L; //   O  B for (float i = 0.; i < steps; ++i) { // P_i vec3 p = o + d * i; vec2 dRM = densitiesRM(p) * L; //  T(P_i -> O) totalDepthRM += dRM; //     T(P_i ->O) + T(A -> P_i) // scatterDepthInt()    T(A -> P_i) vec2 depthRMsum = totalDepthRM + scatterDepthInt(p, sundir, escape(p, sundir, Ra), 4.); vec3 A = exp(-bR * depthRMsum.x - bMe * depthRMsum.y); I_R += A * dRM.x; I_M += A * dRM.y; } } //    // O = o --   // B = o + d * L --   // Lo --     B vec3 scatter(vec3 o, vec3 d, float L, vec3 Lo) { totalDepthRM = vec2(0.); I_R = I_M = vec3(0.); //  T(P -> O) and I_M and I_R scatterIn(o, d, L, 16.); // mu = cos(alpha) float mu = dot(d, sundir); //     return Lo * exp(-bR * totalDepthRM.x - bMe * totalDepthRM.y) //   + I * (1. + mu * mu) * ( I_R * bR * .0597 + I_M * bMs * .0196 / pow(1.58 - 1.52 * mu, 1.5)); } 

关闭着色器

乌云

不错，但是使用一些狡猾的渐变也可以轻松获得这样的图片。

以欺骗的方式，获取云层和上帝的光芒要困难得多。 让我们添加。

这个想法是用气溶胶近似云层，并且只修改密度函数densitiesRM() 。 这可能不是我们想要的物理上正确的（我不知道计算机图形中云中的光的散射实际上是如何接近的）。

 //      const float low = 1e3, hi = 25e2; // vec4 noise24(vec2 v) --       // float t --  float noise31(vec3 v) { return (noise24(v.xz).x + noise24(v.yx).y) * .5; } vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); vec2 retRM = vec2(exp(-h/8e3), exp(-h/12e2) * 8.); //    () if (low < h && h < hi) { vec3 v = 15e-4 * (p + t * vec3(-90., 0., 80.)); //    <s></s>      :     retRM.y += 250. * step(vz, 38.) * smoothstep(low, low + 1e2, h) * smoothstep(hi, hi - 1e3, h) * smoothstep(.5, .55, //  :   .75 * noise31(v) + .125 * noise31(v*4. + t) + .0625 * noise31(v*9.) + .0625 * noise31(v*17.)-.1 ); } return retRM; } 

与期望相反，我们得到的不是美丽的云彩，胜利的甜蜜和粉丝，而是文物。 尝试增加额头上的伪影的步骤并不能完全消除，但是会严重破坏演奏效果。

解决方案 推动内部的拐杖：

• 地平线上最不愉快的文物藏在山后
• 仅在摄像机附近添加云。
• 添加了Monte-Karlovschina，每条行进的射线都偏移了一个随机偏移量： for (float i = pixel_random.w; i < steps; ++i) 。 这增加了非常大的噪点，您必须通过混合连续的帧来暂时消除噪点。

• 需要更多详细信息的区域的步骤数量正在增加（例如，带有云的图层）。 为此，将函数荒谬地分为scatterImpl()和scatterDepthInt() ：

  
  

   //    scatterIn() vec2 depthRMsum = totalDepthRM; float l = max(0., escape(p, sundir, R0 + hi)); if (l > 0.) //   16  depthRMsum += scatterDepthInt(p, sundir, l, 16.); //     4- depthRMsum += scatterDepthInt(p + sundir * l, sundir, escape(p, sundir, Ra), 4.); 

  
  

   //   scatter() //  10    float l = 10e3; if (L < l) scatterIn(o, d, L, 16.); else { scatterIn(o, d, l, 32.); // 8  --     scatterIn(o+d*l, d, Ll, 8.); } 

  
  

与场景几何体对齐

作为距离和阴影函数的传统重新映射的结果，已经获得了到点B的距离L和像素颜色Lo 。 这些值被简单地替换为scatter()函数。 如果光束不靠在几何体上并离开场景，则颜色Lo为零，并且使用escape()计算L认为光束已离开大气层。

像一切。

... ...当然，并非全部。 将所有零件摩擦在一起以使其整体看起来令人信服，这是一个很大的痛苦。 扭曲参数，场景几何形状，噪波功能，轨迹和相机角度只是一堆小题大做。 恐怕我在这里没有很好的建议，除了要花很多小时并把头撞在墙上。

缩小

在处理了着色器最小化器之后 ，最终的着色器分散代码的大小约为1500个字节。 Crinkler将其压缩到约700个字节，大约占所有着色器代码的30％。

育种

我不知道如何计算机图形学。