多项式回归模型

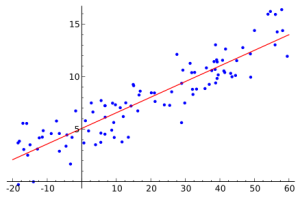
简而言之，数学统计中的回归模型是基于已知数据（即成对的数字）建立的。 这样的对的数量是预定的。 如果您想象一对中的第一个数字是坐标的值 $$$x$ 第二个 $$$y$ ，则此类数字对的集合可以在笛卡尔坐标系中的平面上表示为一组点。 这些数字对不是随机抽取的。 实际上，通常，第二个数字取决于第一个。 建立回归意味着要选择一条线（更确切地说是一个函数），该线尽可能接近（近似）许多上述要点。

这都是为了什么？ 首先，这对于准备所谓的 预测。 经常需要找出 $$$y$ 只知道 $$$x$ 如果它与那些X不同，则在此基础上建立回归。 我将举一个简单的例子。 根据研究的100个不同的人，统计出一个人的成长对其年龄的依赖性。 因此，我们有100对数字{age; 增长}。 同时，“增长”是一个依赖数量，“年龄”是独立的。 通过正确构建回归模型，我们可以根据任何年龄值来确定地“预测”增长。

在实践中，根据情况，在回归模型的构建中将使用线性，抛物线，幂和其他类型的函数。 在数学统计过程中，最常考虑线性回归模型。 有时他们涉及到更复杂的情况-抛物线模型。 概括起来，很容易猜到线性和抛物线模型是更复杂的模型-多项式的特殊情况。 建立回归模型意味着找到将在其中出现的函数的参数。 对于线性回归-两个参数：系数和自由项。

多项式回归可用于数学统计中，以对时间序列的趋势成分进行建模。 实际上，时间序列是取决于时间的一系列数字。 例如，过去一年的平均每日温度或公司的月收入。 模拟多项式的阶数通过特殊方法评估，例如通过级数准则。 在时间序列领域中构建多项式回归模型的目标仍然是相同的-预测。

首先，我们以一般的方式考虑多项式回归问题。 所有推理都基于线性和抛物线回归问题中推理的一般化。 在考虑了这些因素之后，我将继续介绍一种特殊情况-针对时间序列考虑此模型。

让我们给出两个系列的观察结果 $$$x_i$ （独立变量）和 $$$y_i$ （因变量） $$$i = \上划线{1，n}$ 。 多项式方程的形式为

$$

$$y = \ sum \ limits_ {j = 0} ^ k b_jx ^ j，\ \ \ \ \（1）$$

在哪里 $$$b_j$ -该多项式的参数， $$$j = \上线{0，k}$ 。 其中 $$$b_0$ -免费会员。 让我们找到最小二乘（OLS）参数 $$$b_j$ 给定回归。

与线性回归类似，OLS还基于最小化以下表达式：

$$

$$S = \ sum \ limits_ {i = 1} ^ n \ left（\ hat y_i-y_i \ right）^ 2 \ to \ min \ \ \ \ \（2）$$

在这里 $$$\帽子y_i$ -作为点处的多项式（1）的值的理论值 $$$x_i$ 。 将（1）代入（2），我们得到

$$

$$S = \ sum \ limits_ {i = 1} ^ n \左（\ sum_ {j = 0} ^ kb_jx_i ^ j-y_i \ right）^ 2 \至\ min$$

根据功能极值的必要条件 $$$（k + 1）$ 变数 $$$S = S（b_0，b_1，\点，b_k）$ 我们将其偏导数等于零，即

$$

$$S'_ {b_p} = 2 \ sum \ limits_ {i = 1} ^ nx_i ^ p \ left（\ sum \ limits_ {j = 0} ^ kb_jx_i ^ j-y_i \ right）= 0，\ \ \ p = \上线{0，k}$$

将每个等式的左侧和右侧除以2，我们得出第二个和：

$$

$$\ sum \ limits_ {i = 1} ^ nx_i ^ p \左（b_0 + b_1x_i + b_2x_i ^ 2 + \点+ b_kx_i ^ k \右）-\ sum \ limits_ {i = 1} ^ nx_i ^ py_i = 0 ，\ \ \ p = \上标{0，k}$$

打开括号，我们在每个 $$$p$ 表达式，最后一项 $$$y_i$ 向右将两边除以 $$$n$ 。 结果，我们得到了 $$$（k + 1）$ 构成线性正规方程组的表达式 $$$b_p$ 。 它具有以下形式：

$$

$$\ left \ {\ begin {array} {l} b_0 + b_1 \ overline x + b_2 \ overline {x ^ 2} + \ dots + b_k \ overline {x ^ k} = \ overline y \\ b_0 \ overline x + b_1 \上线{x ^ 2} + b_2 \上线{x ^ 3} + \点+ b_k \上线{x ^ {k + 1}} = \上线{xy} \\ b_0 \上线{x ^ 2} + b_1 \上线{x ^ 3} + b_2 \上线{x ^ 4} + \点+ b_k \上线{x ^ {k + 2}} = \上线{x ^ 2y} \\ \ ldots \ ldots \ ldots \ \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \\ b_0 \ overline {x ^ k} + b_1 \ overline {x ^ {k + 1}} + b_2 \ overline {x ^ {k + 2}} + \点+ b_k \上线{x ^ {2k}} = \上线{x ^ ky} \结束{array} \右\ \ \ \ \（3）$$

您可以以矩阵形式重写系统（3）： $$$AB = C$ 在哪里

$$

$$A = \ left（\ begin {array} {ccccc} 1＆\ overline x＆\ overline {x ^ 2}＆\ ldots＆\ overline {x ^ k} \\ \ overline x＆\ overline {x ^ 2 }＆\ overline {x ^ 3}＆\ ldots＆\ overline {x ^ {k + 1}} \\ \ overline {x ^ 2}＆\ overline {x ^ 3}＆\ overline {x ^ 4}＆ \ ldots＆\ overline {x ^ {k + 2}} \\ \ vdots＆\ vdots＆\ vdots＆\ ddots＆\ vdots \\ \ overline {x ^ k}＆\ overline {x ^ {k + 1} }＆\ overline {x ^ {k + 2}}＆\ ldots＆\ overline {x ^ {2k}} \ end {array} \ right），\ \ B = \ left（\ begin {array} {c} b_0 \\ b_1 \\ b_2 \\\ vdots \\ b_k \ end {array} \ right），\ \ C = \ left（\ begin {array} {c} \ overline y \\\ overline {xy} \\ \ overline {x ^ 2y} \\\ vdots \\\ overline {x ^ ky} \ end {array} \ right）$$

现在，我们将上述事实应用于时间序列。 给出时间序列 $$$x_t$ 在哪里 $$$t = \上标{1，n}$ 。 需要建立多项式阶数趋势 $$$k$ ，它会尽可能准确地近似给定的时间序列。 作为自变量 $$$x$ 我们将采取 $$$t$ 基于时间序列的定义。 这些X是代表时间段的一系列自然数。 作为一个 $$$y$ 时间序列值 $$$x_t$ 。 可以看出，元素的值 $$$a_ {ij}$ 系统矩阵 $$独立于 $$$x_t$ 。 因为显然在一般情况下，

$$

$$a_ {ij} = \上线{x ^ {i + j-2}} = \ frac1n \ sum \ limits_ {r = 1} ^ nx_r ^ {i + j-2}，$$

然后是时间序列

$$

$$a_ {ij} = \ frac1n \ sum \ limits_ {r = 1} ^ nr ^ {i + j-2}，$$

在哪里 $$$i，j = \上线{1，（k + 1）}$

物品 $$$c_j$ 自由项的矩阵向量 $$$C$ 通常以

$$

$$c_j = \上线{x ^ {j-1} y} = \ frac1n \ sum \ limits_ {r = 1} ^ nx_r ^ {j-1} y_r。$$

在时间序列的情况下

$$

$$c_j = \ frac1n \ sum \ limits_ {r = 1} ^ nr ^ {j-1} x_r，$$

在哪里 $$$j = \上线{1，（k + 1）}$

因此，通过求解系统（3），我们可以找到多项式趋势的所需参数 $$$b_0，\点，b_k$

为了填充系统矩阵并进行求解，可以在计算机上对趋势建模时使用一种数值方法。 在这种情况下，计算结果将非常准确。

结果，趋势组件将采用以下形式：

$$

$$T_t = \ sum \ limits_ {i = 0} ^ kb_it ^ i，\ \ \ t = 0,1,2，\点$$

还值得注意的是，模拟趋势分量 $$$T_t$ ，不仅针对当前期间确定 $$$[1; n]$ ，而且在将来 $$$t> n$ 。

我立即注意到，多项式回归仅对时间序列的趋势成分进行建模。 完整的时间序列模型还包含其他组件，这不在本文的讨论范围之内。

实际上，我个人没有看到多项式趋势阶数大于2的时间序列。这解释了线性和实用回归模型作为多项式的特殊情况的普遍性。