关于环境或例如某个控制对象的状态的信息可以通过测量表征环境或对象的某些特性的参数的当前值来获得。 为了通过技术手段接收,处理和传输此类信息,必须通过自动测量设备将测量参数的值转换为测量信息信号。 为此,将信息测量通道(
IIC )作为技术手段的组合来实现,每种方法都将履行其特定的功能,从对测量值的感知开始,到最终以易于人类感知或对其进行进一步处理的形式接收测量信息为止。 一切都会好起来,但是沿着信息的路径,干扰
e(t)会叠加在测量信息的有用信号
y(t)上 -时间的随机函数,可以模拟测量传感器,连接线中的电拾取器和随机波动的随机误差测量参数和其他因素。
基于此,IIC中信息的主要处理会出现问题-从随机干扰e(t)中过滤测量信息的信号y(t)。 基本上,滤波方法基于函数y(t)和e(t)频谱的差异,并且干扰被认为是更高频率的。
所实现的最佳滤波器的综合是一项复杂的任务,其解决方案需要准确说明有用信号和干扰的特性。 因此,在实践中,通常指定滤波器的传递函数并将其限制为使用简单滤波算法的参数合成。
过滤方法在软件级别和硬件级别均执行。 例如,在BMP280(BOSCH)传感器中,可以在硬件级别连接IIR滤波器,并在必要时更改滤波器系数k [1]。
IIR滤波器
具有无限脉冲响应的滤波器是递归滤波器,并根据先前输入和输出采样的值来计算输出信号。 从理论上讲,IIR滤波器的脉冲响应永远不会达到零,因此输出的持续时间是无限的。
通常,我们将用于过滤一维标量数字滤波器的算法写为[2]:
,(1),
其中
T是一个变量的标量函数。
函数
T取决于当前输入信号x [n],以及前一个:输入信号的M个样本

和N个输出信号样本
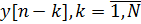
IIR滤波器的输出由以下形式的差分方程描述:

(2)
其中x [n],y [n]分别是滤波器的输入和输出,{
}是一组直接系数,M是一组直接系数,{
}是一组反系数,N是反系数的数量。
将z变换应用于方程式(2)的两边,我们获得:
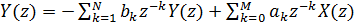
(3)。
然后,过滤器的传递函数将如下所示:
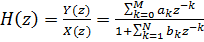
(4)
一维IIR滤波器的滤波算法
一般而言,一维标量固定递归滤波器的滤波算法如下所示:
。 (5)
现在,我们以[1]的形式编写IIR滤波器的差分方程:

(6)
其中k是滤波器系数;
或
(7)
在哪里

分别是逆滤波器系数和正滤波器系数。
从(7)可以明显看出,在k = 1时,滤波器的输出信号将重复输入,并且随着滤波器系数k的增加,前一个滤波信号的权重趋于1,而测量值的权重趋于0。
算法(6)在Arduino软件(IDE)开发环境中的软件级别上作为BMP280传感器的绝对大气压力信息测量通道的示例实现,清单1。IIC组件的电气连接图如图2所示。 图1给出了IIC原型绝对大气压的总体视图。 2.原型可以通过旋转电位计的旋钮在1 ... 50范围内以1为增量更改滤波器系数。 液晶显示屏的符号显示测得的压力值(对于k = 1)或滤波后的值(对于k = 2 ... 50),以及滤波系数k。
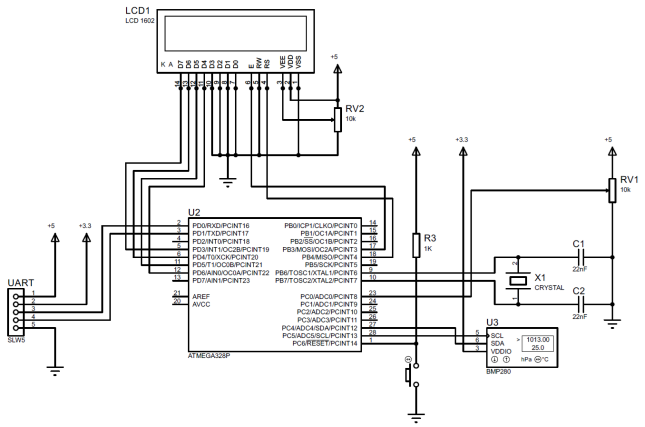 图 1-IIC原型组件的接线图
图 1-IIC原型组件的接线图 图 2-IIC原型的一般视图
图 2-IIC原型的一般视图用于研究IIR滤波器的Python脚本
清单2显示了用于检查IIR过滤器的Python脚本。 滤波器系数k写在脚本中。 从虚拟COM端口顺序读取测量的压力值并进行过滤。 实时在图形窗口和控制台上显示测量参数的测量值和滤波值。 实验结果由表格记录在文件中,测量和过滤后的值的时间轴显示在图形窗口中。
清单2 import numpy as np import matplotlib.pyplot as plt import serial from drawnow import drawnow import datetime, time k = 6.0
实验结果
: 33 : 6 : COM6 : n - ; P - , ; n P 0 100490.00 100490.00 1 100488.00 100489.71 2 100487.00 100489.33 3 100488.00 100489.14 4 100488.00 100488.97 … 30 100486.00 100488.14 31 100492.00 100488.70 32 100489.00 100488.74 : 16.028, c : 0.500875, c 275_count.txt Ctrl-C,


结论
上面的过滤算法在软件实现中非常简单,并且在实践中可以与本文中讨论的类似在IIC中使用。
Losikhin D.A.,s.v. 咖啡厅 城市 。
信息来源
- BMP280数字压力传感器
- 无限冲激响应滤波器