引言
迄今为止,确定比空气轻的飞机(LALV)的上升和下降速度几乎是设计此类装置时要承担的重要任务。
例如,大量出版物致力于LALF,仅在我们的资源上有两篇非常有趣的文章[1,2],它们与飞艇和平流器的特定设计实例有关的发展历史。 然而,很少有此类设备的垂直飞行动力学的计算,从而至少可以大致确定轻小武器的上升和下降速度。
最后的陈述需要一定的解释,因为有经验的读者会记住学校的物理课程,其中解决了上升高度和填充比空气轻的气体或飞行过程中被加热的空气本身的气球的其他参数的问题。
所有这些任务都是基于两个力的相等性:重量力和浮力。 气体被认为是理想气体,其参数根据门捷列夫·克拉珀龙定律进行计算。 但是,即使简单地计算出空气阻力的第三力,也已经导致了微分方程组的建立,而这在解析上是无法解决的。 还必须考虑大气密度随上升高度和温度的变化。
另外,如果您不仅需要考虑球的上升,还需要考虑球的冻结及其下降到地面的问题,那么这根本不是孩子的任务。 我希望考虑使用Python解决类似问题的方法,不仅将有助于扩展物理知识,而且还将有助于Python本身的编程语言的普及。 我在此资源的出版物中尝试做的事情。
具有球状壳体的LALV飞行的数学模型,其体积不会随高度变化
我们仅限于考虑在以下力的作用下其质心的运动:重力(
G ),阿基米德力(
Fa )和气动阻力(
Fc )。 我们写出通过运动和空气环境参数确定力的关系[3]:
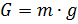

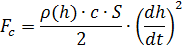
在上面的公式中,使用的符号是:h是球的高度,dh / dt是垂直速度,m是质量,g是重力加速度,W是球的体积,c是阻力系数,S是特征阻力区域(中间区域)。
空气密度对高度的依赖性将被假定为指数:
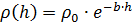
在哪里
-零高度处的空气密度,b-系数。 重力是向下的,阿基米德力是向上的,而空气阻力一直是“相对运动”的方向,因此,在运动方程中正确包含此力需要引入一个因数
。
但是,就我们的目的而言,这一事实并不重要,我们将自身限制为仅考虑升起球的阶段,即将气动阻力向下指向时,因此将在运动方程式中将其考虑为负号。 现在,运动方程可以写成:

,(1)
另外,假设气球是半径为R且具有密度的均质体
。 然后将确定其空气阻力的区域的大小定义为
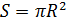
音量为

和质量分别为

。
现在很明显,方程式(1)的每个项都包含S.作为因子,因此,运动方程式的每个项都可以减少S倍。

,(2)
我们引入以下符号:

;

;
并以以下非线性方程组的形式重写(2):
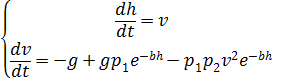
,(3)
对LALV气温上升速度和高度的影响
为此,我们首先使用以下关系式求解系统(3),其中大气空气的密度与高度有关,而无需考虑温度:
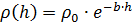
让我们重复系统(3)的解决方案,但使用该关系式来确定空气密度对海拔和温度的依赖性:

其中:b = 0.000125是与1 / m。的空气密度相关的常数。
a = 0.0065是与空气温度有关的常数,单位为K / m。
-海平面温度。
我们得到:
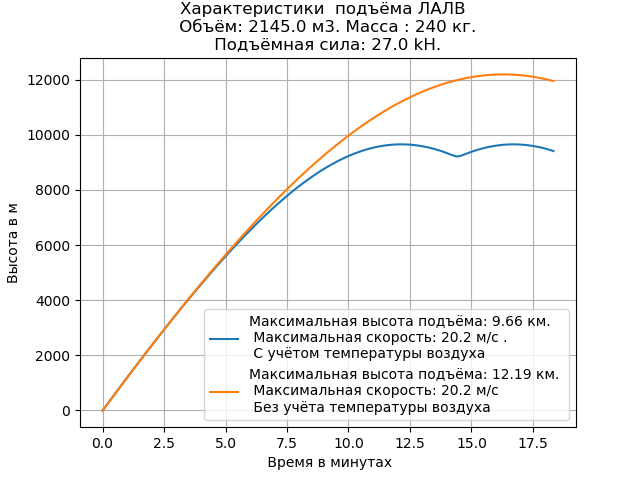
考虑到温度,LALV升降机高度的计算值小于没有。 设备的提升速度保持不变。
确定从开始到着陆的SALV飞行各个阶段的特征
要构建LALV飞行计划,请考虑以下时间段的条件:
上升 -
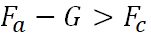
;
挂 -
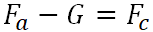
;
着陆 -

。
我们得到:
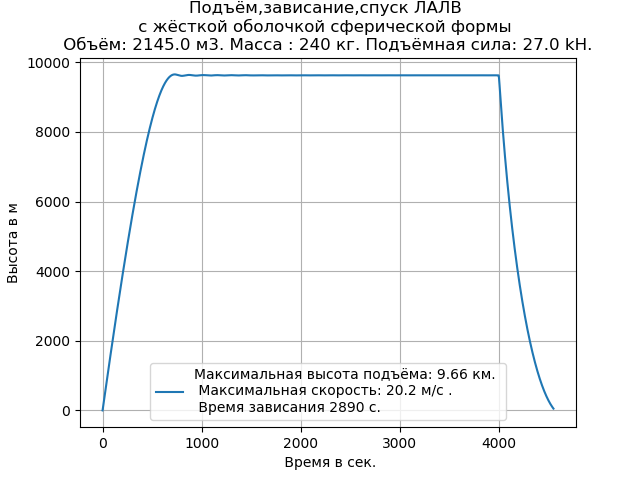
从程序的图形和清单如下所示,要进行计算实验,只需输入必要的初始数据即可。
带壳的LALV飞行的数学模型,其体积随高度而变化
这样的LALV包括平流器。 平流层气球无法完全充入氦气,从而使其具有最大的升力,这将使其外壳变成球形。 由于内部和外部压力差的增加,这种高海拔的球可能会爆裂。
由于这些原因,为了计算最大可达到的举升高度,引入了其体积的两个值:分别为最小Vmin和最大Vmax。 考虑到引入的变量以及空气密度对高度的依赖性,浮力Fa和重力Ft的比率采用以下形式:

,(4)
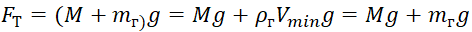
,(5)
其中:M是平流层气球的外壳和设备的质量;
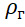
是氦气的密度。
等式(4)和(5),假设壳V的体积是LALV高度的函数,我们得到以下比率:
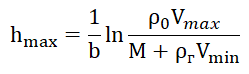
。 (6)
关系(6)中包含的参数的数值在列表中给出,用于构造图形,仅出于指定目的给出图形。
我们得到:
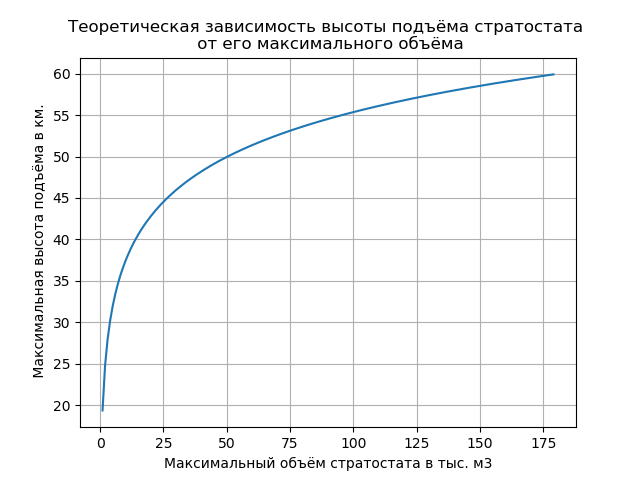
通过更改程序列表中列出的LALV参数,可以得到给定的图并在设计过程中选择所需的最大外壳体积。 使用创建此类设备的丰富经验对结果进行优化。
结论:
- 获得了两种类型的比空气轻的飞机的数学模型,其允许进行计算实验以在理想的空气环境下评估此类设备的参数。
- 所提出的用于微分方程组数值解的多阶段方案允许在悬停和下降的上升阶段获得比空气轻的飞机的垂直轨迹。
参考文献
- 关于飞艇的几句话
- 在通往太空的路上。 层流器
- 于志科夫 现代Fortran。 -圣彼得堡:王冠印刷,2004年。-288羽