“但是我们制造火箭！”在
上一篇文章中，我检查了是否可以使用优化的“标准方法”自动调整模糊控制器。 事实证明这是可能的，并且自动调整的结果非常令人满意。 至少对于使用其模型的火箭而言。
对于对象参数在宽范围内变化的非平稳控制对象，模糊控制器可能无法在所有操作范围内提供足够的控制质量。 在这种情况下，必须使用具有“多通道调整”功能的模糊控制器。
让我们检查是否可以使用标准优化方法配置这样的调节器。
考虑综合多通道调整的模糊控制器，以使弹道导弹的俯仰角稳定。 如评论所述，导弹将是FAU-2。 我们使用来自V. Gostev的同一本书中的示例。 “自动控制系统中的模糊调节器。”
本文中使用的所有术语均取自本书，可能与自动控制理论的严格术语不符。
问题陈述
使用大量本地控制系统的弹道导弹基本上是非平稳的控制对象。 将火箭描述为控制对象的传递函数与有翼飞机的传递函数的不同之处在于，它们具有不稳定的连杆，因此不受控制的火箭沿着编程路径的运动将是不稳定的。
下面我们考虑弹道导弹在俯仰角（纵向运动通道）中的稳定系统。 该系统由以下功能上必要的元素组成：
比较元件（带有以Kp系数为特征的电位传感器的自由陀螺仪）；
功率放大器Ku和液压转向器。
以俯仰角作为火箭的出口坐标
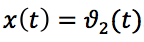
，对于输入坐标-转向角
，我们以以下形式定义传递函数：
（控制对象中包括模拟舵机和火箭）传递函数的参数将是时间相关的多项式。 从数学上讲，它们可以由多项式确定：
该任务假定飞行开始时间为6秒。 多项式值以6秒的间隔被接受。
非平稳振荡环节的数学模型由微分方程描述：
非恒定强迫连杆的数学模型由微分方程描述：
模糊控制器输入端的失配误差是设定值与所需俯仰角之间的差。
该模型的结构图如图1所示。为了理解模型形成的原理，通讯线根据链接的方程式指示变量
X1，X及其导数（
X1''，X1''，X' ）。 绿色矩形表示模型电路中与振荡链接相对应的部分，而黄色矩形是强制链接。
参数
a（t），b（t），c（t），r（t）以“放大”类型的块形式以放大系数的形式设置。 参量
在积分链接的增益中设置。
图1.模型的结构图。软件路径，给定俯仰角u（t）= 1 + 0.5sin（πt/ 30）。
飞行过程中火箭参数的变化图如图2所示。
t = 6的值作为飞行的起点；在多项式函数中，值（time + 6）用于计算参数，其中time是当前的模拟时间。
图2.火箭参数变化图。模糊逻辑控制器
作为基于模糊逻辑的控制器，我们使用图3所示的控制器。给定的俯仰角和实际导弹俯仰角之间的不匹配将应用于输入。
每个量化步骤的块延迟提供了将连续信号转换为离散信号的离散化，采样步长为0.01秒。
使用另外两个延迟，通过离散化步骤上的差分方法计算一阶和二阶导数偏差。
分阶段单元计算偏差，变化率和加速度的项值。 （有关更多信息，请参见
前面的文本 ）。 在每个定相块的出口处，我们获得了语言变量项的向量。 （见表1）
| 语言变量 | 条款 |
| 偏差 | 更多
规范
少一点
|
| 变化率 | 正在成长
不变
正在下降
|
| 更快的变化 | 正在增加
不变的
减少
|
解复用器块将向量解析为单独的项，然后根据模糊推理规则将其传输到逻辑处理块。
模糊推理的结果还具有三个语言变量：“减少”，“不变”，“增加”。 以下推理规则以图表形式编写。
- 如果更多，并且增长和增长率增加 => 减少 。
- 如果规范 ，并且不改变并且是常数 =>，我们就不改变 。
- 如果减少 跌倒且下降率增加 => 增加 。
图3.基于模糊逻辑的调节器方案。在脱硝中，将具有共同底数的三角函数用作隶属函数（参见图4）。
图4.具有共同基数的三角定相功能。假设函数相对于0是对称的，在这种情况下，为了描述三个三角函数，
Max的一个值
就足够了。 对于图中所示的最大值，Max = 30。
相同的隶属函数用于输出。
为了完整定义调节器，有必要为相位可变块设置最大值：
-deltaMax-最大偏差；
-divMax-偏差的最大导数；
-div2Max-偏差的最大二阶导数；
-uMax-最大控制动作。
全过程优化
采取的最大控制作用等于uMax-70。
因此，我们仍然需要为移相功能选择3个参数。
在这个问题中，失配是在模型时间的零时刻由一个步长进给的，u（t）= 1 + 0.5.sin（πt/ 30）。
在给定的俯仰角u（t）= 1 + 0.5sin（πt/ 30）的情况下，编程的轨迹会在过渡过程的第一秒产生逐步影响，因为在执行前一项任务的实验过程中发现，调节器已调整为平滑的控制过程，并具有逐步作用无法提供过渡过程所需的质量。
因此，为了进行优化，我们形成3个条件：
- 瞬态时间-我们必须尽快到达给定的程序路径。
- 标准偏差。
- 切换次数-在前一项任务的实验中，当控制系统的输出端出现控制动作的高频振荡时，我们可以选择。
优化块的一般方案如图5所示。
图5.优化块的方案。优化块输入参数：
-与给定俯仰角的偏差。
-监管影响。
为了计算瞬态时间，使用了一个将当前模型时间应用于其中一个输入的开关。 在该块之后，存在量化周期的延迟，该延迟的值将传输到第二个输入。
作为开关，使用偏差模块。 如果偏差模块大于设定的切换值（0.02），则在块上输出当前时间；如果模块小于设定值，则将偏差较大时存储的时间传输到输出。 如果进一步的偏差再次超出限制，我们将再次获得时间。 因此，在出口处，总是有偏差超过设定值的最后一次。
作为切换单元，控制动作的符号从+变为-。 为了计算切换次数，我们使用“沿前部的脉冲”块，当输入从0更改为1时，在积分步骤中给出持续时间的脉冲，该脉冲由积分器计算。 在该区块的出口-切换次数。
-优化块以最小化所有三个参数的方式选择要优化的参数的值：
-deltaMax-最大偏差；
-divMax-偏差的最大导数；
-div2Max-偏差的最大二阶导数。
结果是优化了整个过渡过程。
开始优化过程后，我们为模糊控制器获得了以下最佳参数：
-deltaMax = 0.185–最大偏差；
-divMax = 0.278-偏差的最大导数；
-div2Max = 1.291-偏差的最大二阶导数。
优化过程的结果如图6所示。
图6a。 过渡过程。
| 
图6b。 控制选项。
|
可以看出，总体上说，优化是成功的，但是在整个过程中几乎都存在与给定俯仰角的偏差。 放大的偏差图显示，优化和过渡过程完成后的偏差在0.015-0.02之间。 （见图7）
图7.控制过程中的偏差。按飞行段进行优化。
让我们尝试通过为火箭飞行的不同部分选择模糊控制器的参数来改进过程。
第一部分是从给定路径开始到退出的时间。 基于偏差图，与初始逐步效果相关的过渡过程在20秒处结束。 （见图7）。 在本节中，将进行过渡过程的时间优化。
将计算结束时间设置为20秒。 我们将执行优化，从标准中删除标准偏差。 我们将根据过渡过程的时间和切换次数进行优化。 优化框图如图8所示。
图8.飞行第一阶段的优化方案。飞行第一阶段长达20秒的自动优化产生了以下参数用于模糊调节：
-deltaMax = 0.056–最大偏差；
-divMax = 0.0968-偏差的最大导数；
-div2Max = 0.987-偏差的最大二阶导数。
优化后的过渡过程如图9所示。
较大的偏差如图10所示。
图9a。 过渡过程。
| 
图9b。 控制选项。
|
图10.航班第一航段的较大比例偏差。曲线图表明，过冲减小，过渡过程结束后的偏差小于0.005。
为了在下一个飞行部分中进行优化，我们将使用在第一部分中获得的保存状态执行仿真。
仿真发生在弹道导弹飞行20到40秒之间，整个过程进行了优化。
由于我们已经在第二部分的开头完成了转换过程，因此仅通过偏差和开关数量进行优化。 优化框图如图11所示。
图11.第二段飞行的优化方案。飞行第二阶段从20秒到40秒的自动优化产生了以下参数用于模糊调节：
-deltaMax = 0.056–最大偏差；
-divMax = 0.0974-偏差的最大导数；
-div2Max = 0.980-偏差的最大二阶导数。
在给定参数的情况下，俯仰角与给定角度的偏差会在整个飞行的第二时间段内减小。 但是，如果我们使用在飞行的第二部分中通过优化获得的参数来控制最多66秒，那么可以看出，精度在40秒后开始降低，偏差开始增加（参见图12）。
图12.弹道导弹控制过程，其设置针对20-40秒的飞行进行了优化。对飞行的第三段重复优化。 保存结果40秒。
我们使用它们在40到66秒的时间段内开始和优化。
最后一次飞行段从40到66秒的自动优化产生了以下参数用于模糊调节：
-deltaMax = 0.0146–最大偏差；
-divMax = 0.0157 –偏差的最大导数；
-div2Max = 0.555-偏差的最大二阶导数。
优化后的弹道导弹飞行最后部分的控制过程图如图13所示。
图13.飞行最后一站的弹道导弹控制过程。图13显示，与针对第二飞行段优化的设置相比，使用新设置，飞行时间间隔40-66秒的偏差不会增加（请参见图12）。
因此，我们获得了飞行三个部分的模糊控制器的设置。 让我们创建一个模式开关，它将在飞行过程中切换控制器设置。 模式切换电路如图14所示。
图14.模糊弹道导弹控制器的模式切换。切换模式将及时发生，在上部，一个简单的逻辑电路将当前模型时间与切换点进行比较。 结果，在多路复用器中形成三个值的控制矢量。 在此向量中，值1位于当前时间间隔的位置。
通过优化方法较早计算出的模糊控制器的参数打包成三个值的向量。
在三个值的采样块的帮助下，选择一个与控制矢量中的1对应的值，因此，当时间变化时，传递到模糊控制器的参数会根据当前飞行区间而变化。
为了清楚起见，在图中显示了通过通信线路传输的值。 该图对应于弹道导弹飞行的最后一部分。 时间超过40秒。 集合中的最后一个参数的控制向量（0，0，1）被提供给控制器。
图15显示了通过切换调节器的参数来控制火箭的俯仰角的仿真结果。
图15a。 过渡过程。
| 
图15b。 控制选项。
|
结论：可以通过优化方法将基于模糊逻辑的控制器配置为在参数切换模式下工作。
与具有恒定参数的控制器的操作相比，在给定示例中使用可变参数时的偏差减少了3-5倍。
可以
下载独立研究项目的存档
...