神经网络，基本操作原理，多样性和拓扑

神经网络已经彻底改变了模式识别领域，但是由于操作原理的可解释性不明显，因此它们并未用于医学和风险评估等领域。 它需要网络的直观表示，这将使其不是黑盒，但至少是“半透明的”。 神经网络，流形和拓扑中的Cristopher Olah演示了神经网络操作的原理，并将其与拓扑和多样性的数学理论联系起来，这是本文的基础。 为了演示神经网络的操作，使用了低维深度神经网络。

了解深度神经网络的行为通常不是一件容易的事。 探索低维深度神经网络比较容易，低深度神经网络是每层只有几个神经元的网络。 对于低维网络，您可以创建可视化文件以了解此类网络的行为和培训。 这种观点将提供对神经网络行为的更深入了解，并观察将神经网络与称为拓扑的数学领域结合在一起的联系。

由此产生了许多有趣的事情，包括能够对某些数据集进行分类的神经网络的复杂性的基本下限。

通过示例考虑网络原理

让我们从一个简单的数据集开始-平面上有两条曲线。 网络任务将学习对属于曲线的点进行分类。



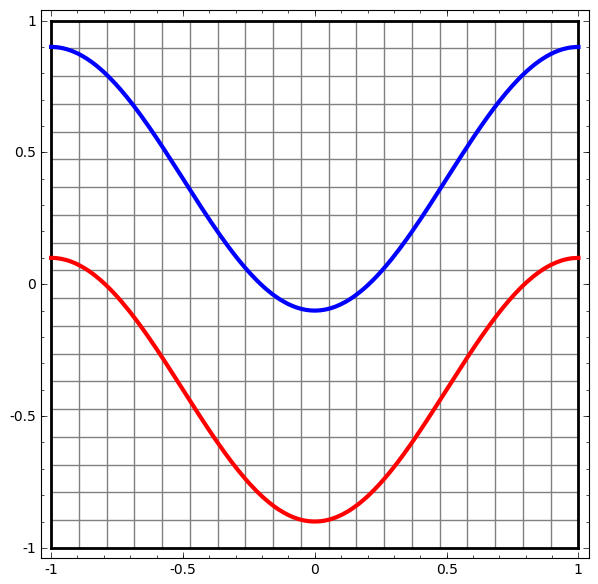
可视化神经网络行为的一种明显方法，是查看算法如何对数据集中的所有可能对象（在我们的示例中为点）进行分类。

让我们从具有一个输入和输出层的最简单的神经网络类开始。 这样的网络试图通过将它们划分为一行来分离两类数据。



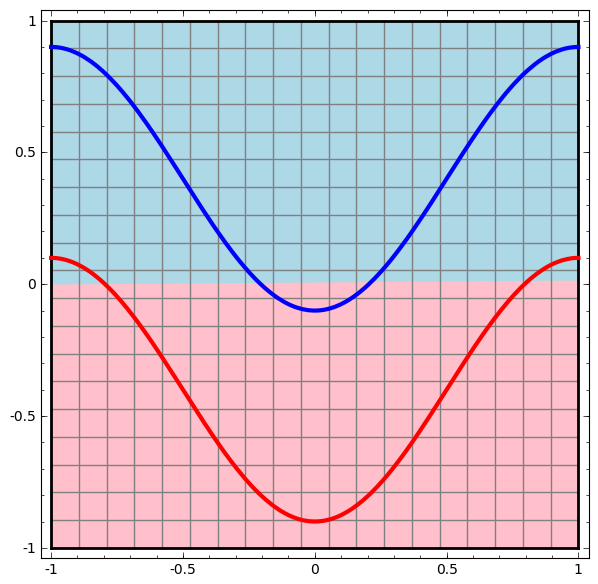
在实践中不使用这种网络。 现代神经网络通常在其输入和输出之间有几层，称为“隐藏”层。

简单的网络图

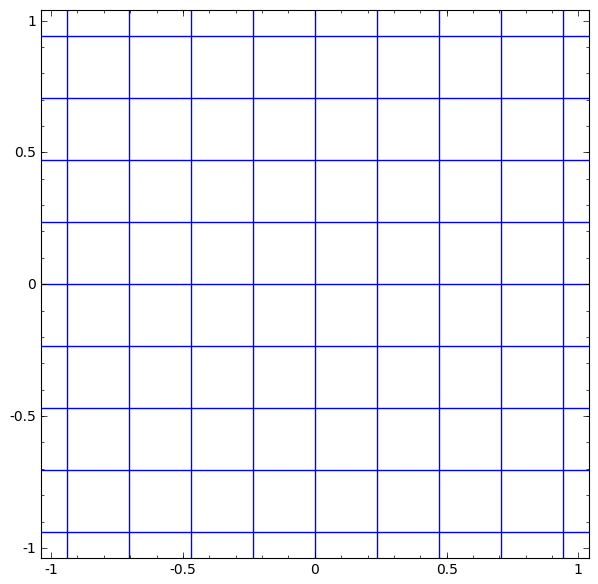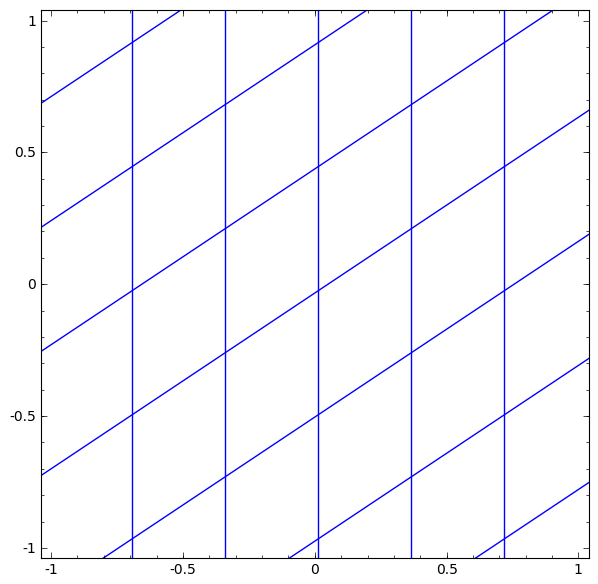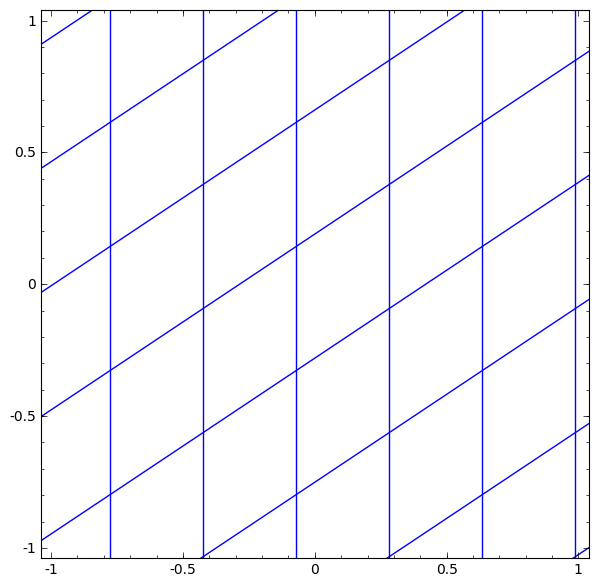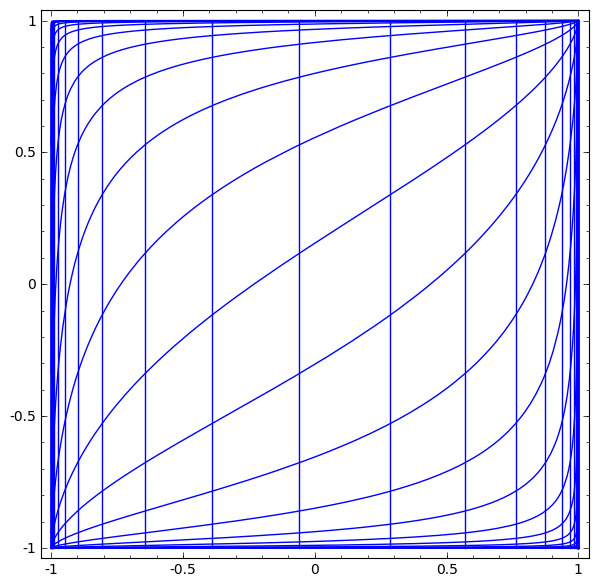
我们可视化该网络的行为，观察它在其领域中不同点的作用。 隐藏层网络将数据与比直线更复杂的曲线分开。



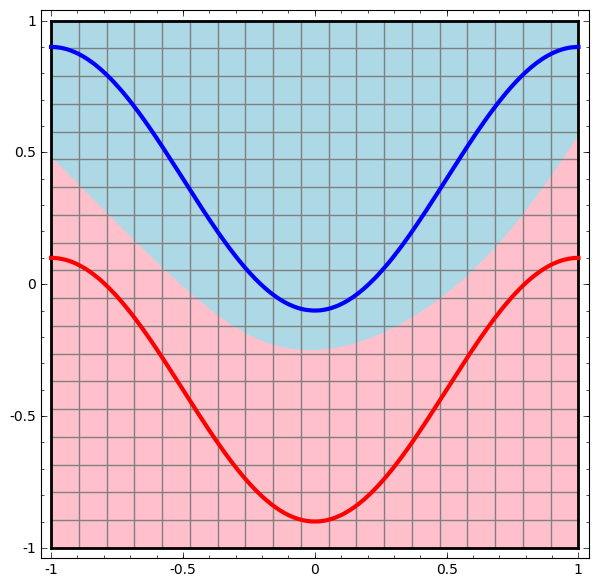
在每一层中，网络都会转换数据，从而创建一个新视图。 我们可以在每个视图中看到数据，以及带有隐藏层的网络如何对它们进行分类。 当算法达到最终表示形式时，神经网络将在数据上绘制一条线（或在更高维度上为超平面）。

在先前的可视化中，将考虑原始视图中的数据。 您可以通过查看输入层来想象。 现在，将其转换为第一层后再考虑。 您可以通过查看隐藏层来想象这一点。
每次测量都对应于该层中神经元的激活。



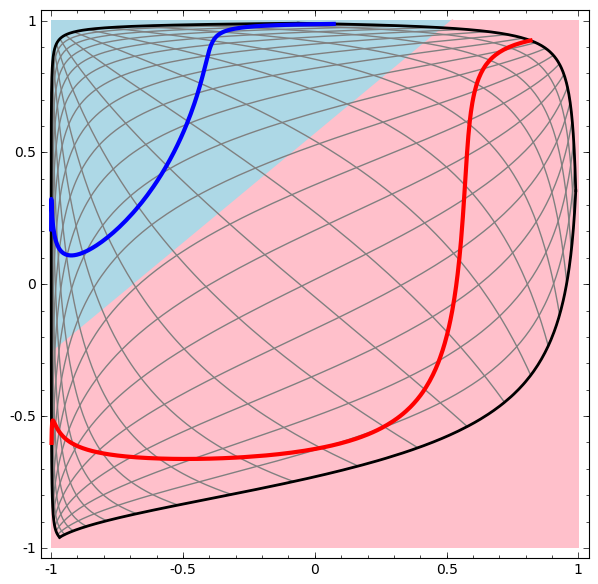
在视图上训练隐藏层，以便数据可线性分离。

连续层渲染

在上一节中描述的方法中，我们通过查看与每一层相对应的表示来学习理解网络。 这给了我们离散的视图列表。

不平凡的部分是了解我们如何从一个转移到另一个。 幸运的是，神经网络层具有使之成为可能的属性。
神经网络中使用了许多不同类型的层。

考虑一个特定示例的tanh层。 Tanh-tanh层（Wx + b）包含：

1. “权重”矩阵W的线性变换
2. 使用向量b进行翻译
3. tanh的现场应用。

我们可以将其表示为以下连续转换：



该操作原理与由仿射变换组成的其他标准层非常相似，然后逐点应用单调激活函数。
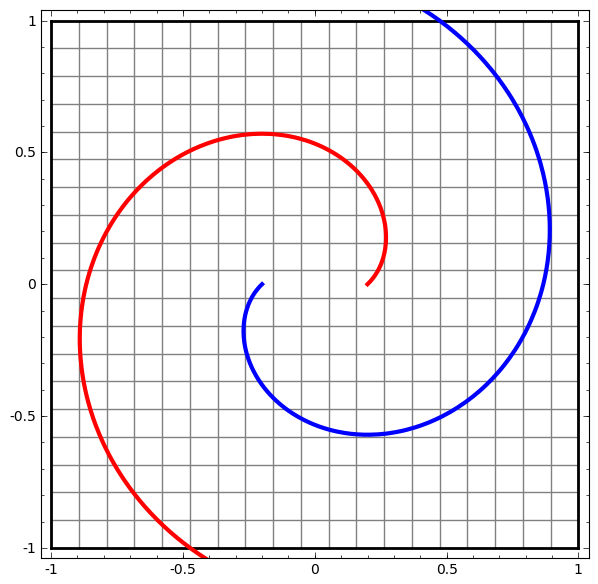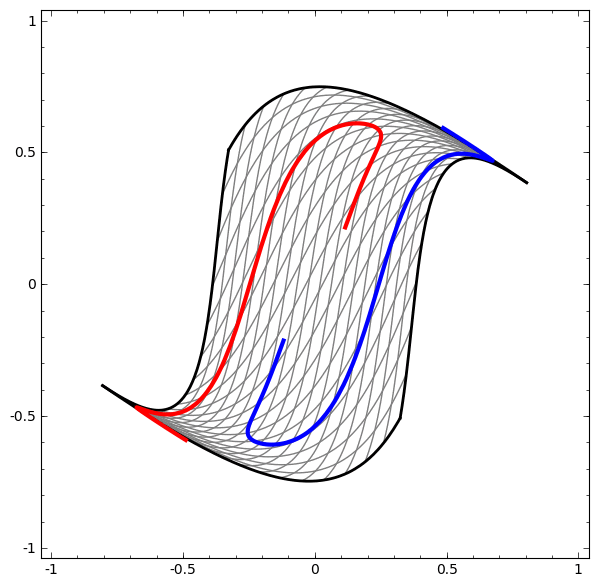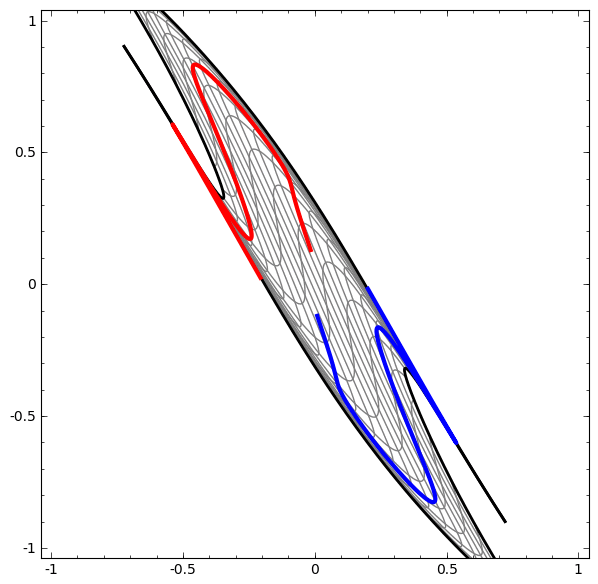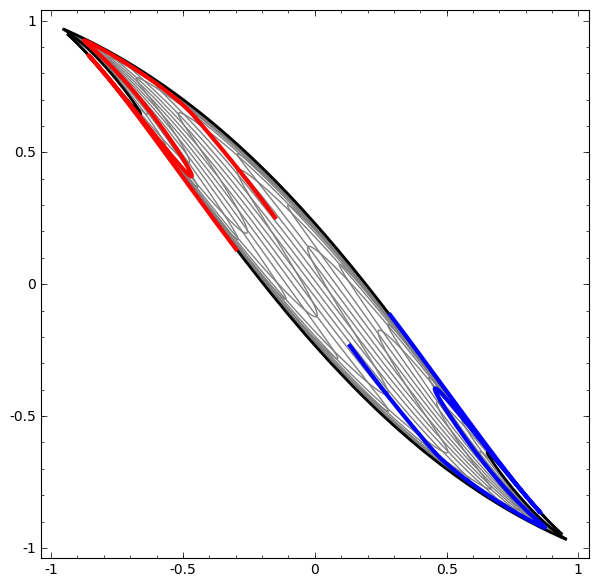
此方法可用于了解更复杂的网络。 因此，以下网络将使用四个隐藏层稍微缠结的两个螺旋进行分类。 随着时间的流逝，可以看出神经网络从原始视图移动到了该网络为数据分类所研究的更高层次。 螺旋线最初是纠结的，但是到最后它们是线性可分离的。



另一方面，下一个网络也使用多个级别，但不能对两个螺旋进行分类，而这两个螺旋更加纠结。



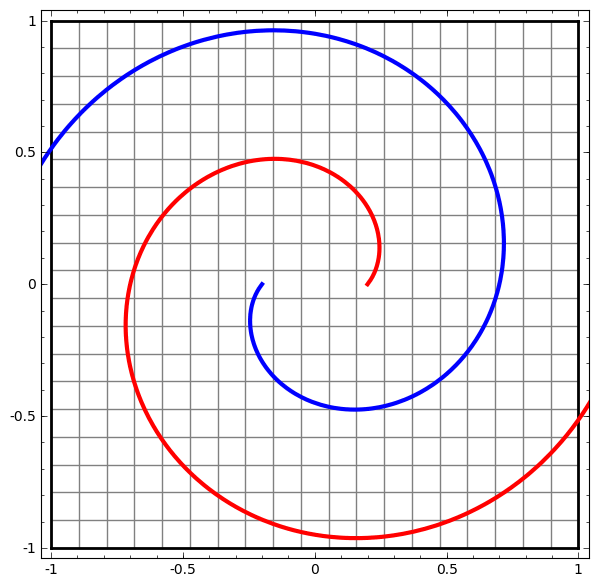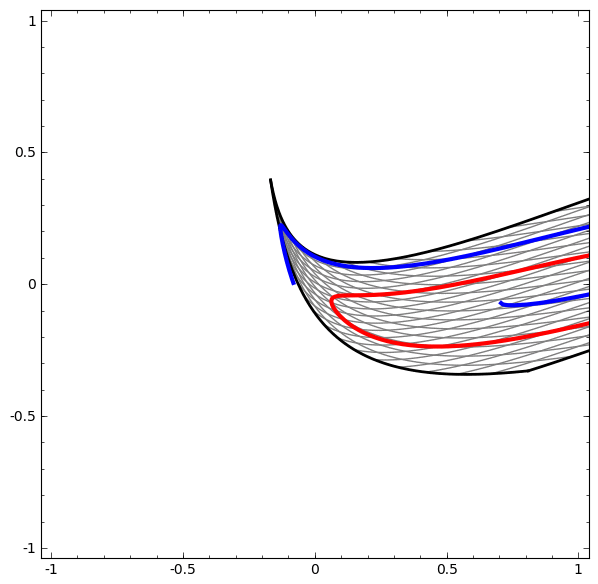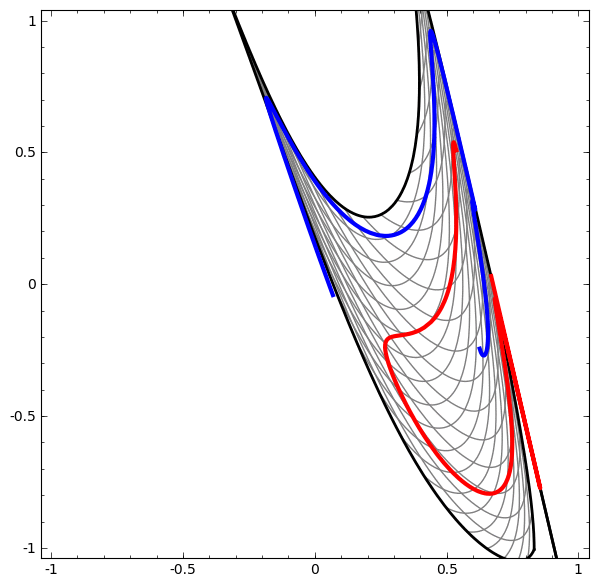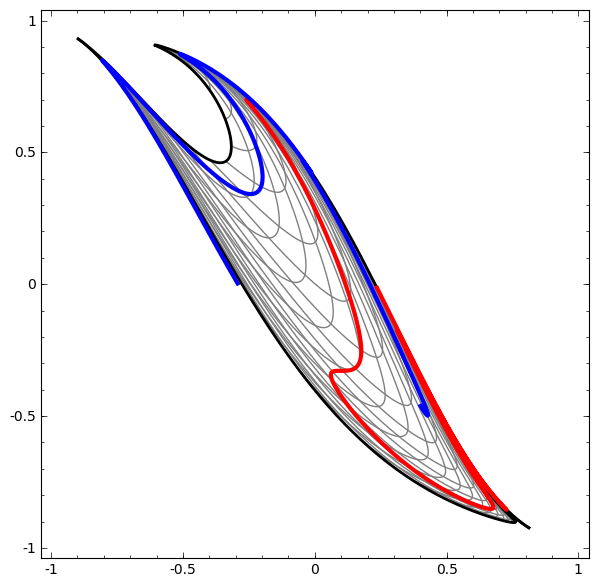
应该注意的是，由于使用了低维神经网络，因此这些任务的复杂性有限。 如果使用更广泛的网络，则会简化问题的解决。

唐层

每一层都拉伸并压缩了空间，但它从未切割，不会破裂和折叠。 直观地，我们看到拓扑属性保留在每一层上。

这种不影响拓扑的变换称为同态（Wiki-这是代数系统A的映射，保留了基本运算和基本关系）。 从形式上讲，它们是双向的连续函数。 在双射映射中，一组的每个元素恰好对应于另一组的一个元素，并定义了具有相同属性的逆映射。

定理

如果权重矩阵W不退化，则具有N个输入和N个输出的层是同态的。 （您需要注意域和范围。）

拓扑和分类

考虑具有两个类A，B⊂R2的二维数据集：

A = {x | d（x，0）<1/3}

B = {x | 2/3 <d（x，0）<1}



A红，B蓝

要求：神经网络无法在没有3个或更多隐藏层的情况下对该数据集进行分类，无论其宽度如何。

如前所述，使用S形函数或softmax层进行分类等同于尝试找到在最终表示形式中将A和B分隔开的超平面（或本例中的线）。 只有两个隐藏层，网络在拓扑上无法以这种方式共享数据，并且注定会失败。
在下一个可视化中，当网络与分类线一起训练时，我们观察到一个潜在视图。



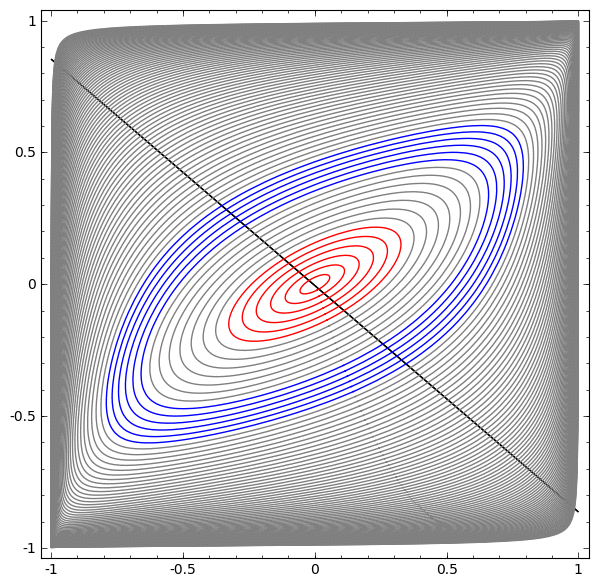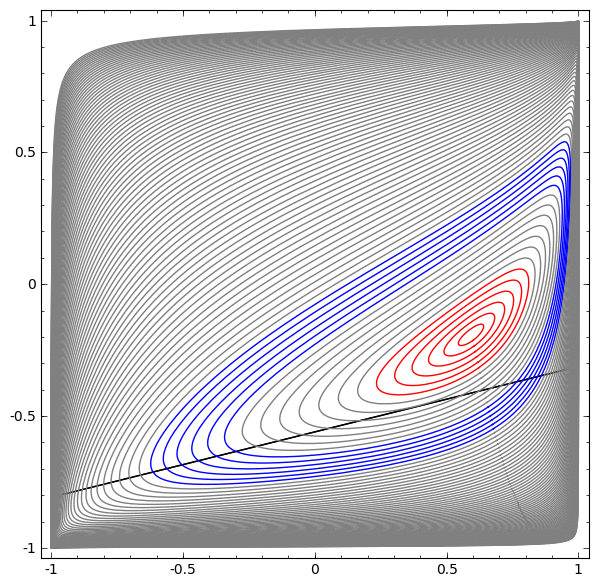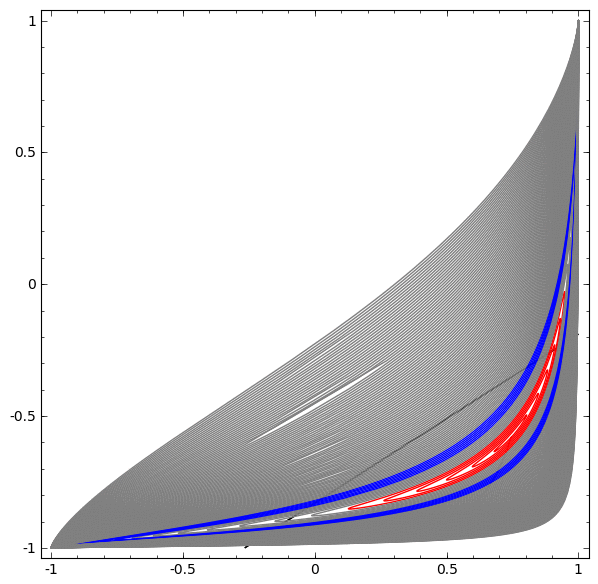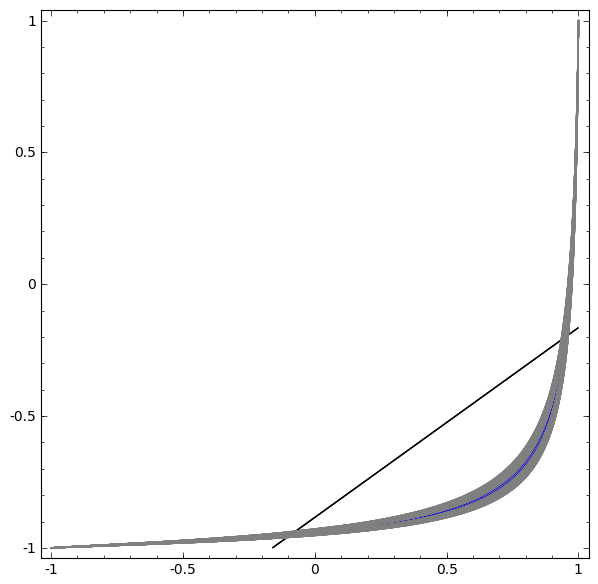
对于这种培训网络来说，还不足以实现百分之一百的结果。
该算法属于非生产性局部最小值，但能够实现约80％的分类精度。

在此示例中，只有一个隐藏层，但是它不起作用。
声明。 每个层都是同构的，或者该层的权重矩阵具有行列式0。


如果我们添加第三个隐藏元素，问题将变得微不足道。 神经网络识别以下表示：



该视图使使用超平面分离数据集成为可能。
为了更好地了解发生了什么，我们来看一个更简单的数据集，它是一维的：



A = [-1 / 3,1 / 3]
B = [-1，-2/3]∪[2 / 3,1]
如果不使用两个或多个隐藏元素的图层，就无法对该数据集进行分类。 但是，如果我们使用包含两个元素的网络，我们将学习如何将数据表示为一条良好的曲线，该曲线允许我们使用一条线来分隔类：



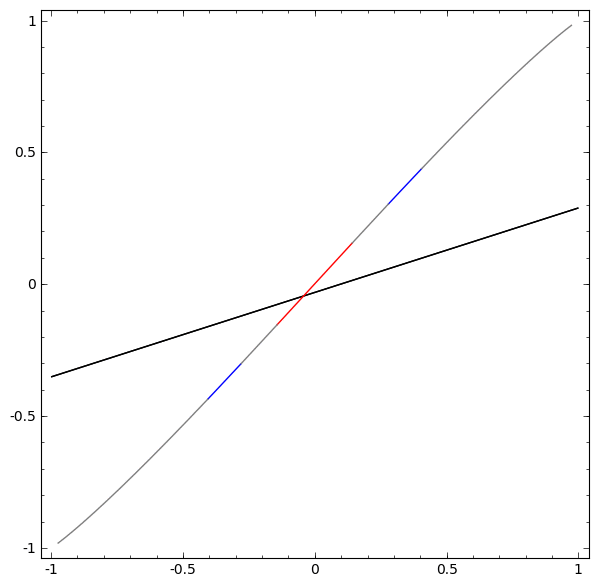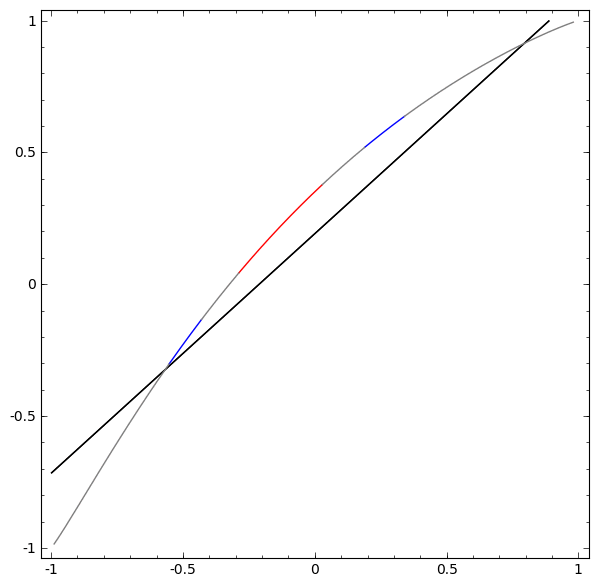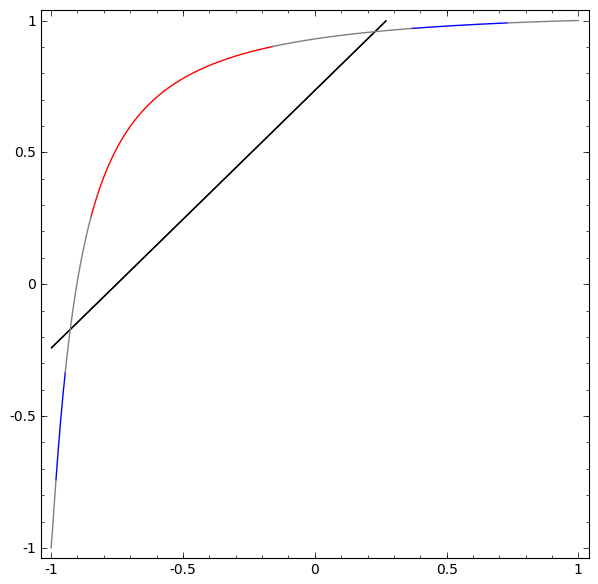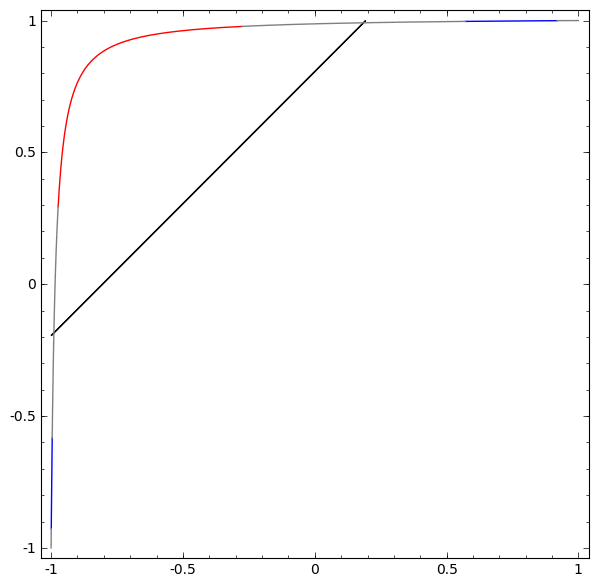
这是怎么回事？ 当x> -1/2时，一个隐藏元素学会射击，而当x> 1/2时，一个隐藏元素学会射击。 当第一个触发但第二个触发时，我们知道我们在A中。

多样性猜想

这是否适用于现实世界中的数据集，例如图像集？ 如果您认真对待多样性假设，那么我认为这很重要。

多维假设是自然数据在植入空间中形成低维流形。 从理论上[1]和实验上[2]都有理由相信这是正确的。 如果是这样，则分类算法的任务是分离纠缠的歧管束。

在前面的示例中，一个类完全包围了另一个类。 但是，各种各样的狗图像不可能完全被猫图像集合所包围。 但是，还有其他更合理的拓扑情况可能会出现，正如我们将在下一部分中看到的那样。

连接和同态

另一个有趣的数据集是两个相连的花托A和B。



像我们之前研究的数据集一样，如果不使用n + 1个维度（即第四维），就无法对这个数据集进行划分。

在结的理论中，在拓扑学领域研究连接。 有时，当我们看到一个连接时，并不清楚是否是不连贯的（很多东西纠结在一起，但可以通过连续变形分开）。



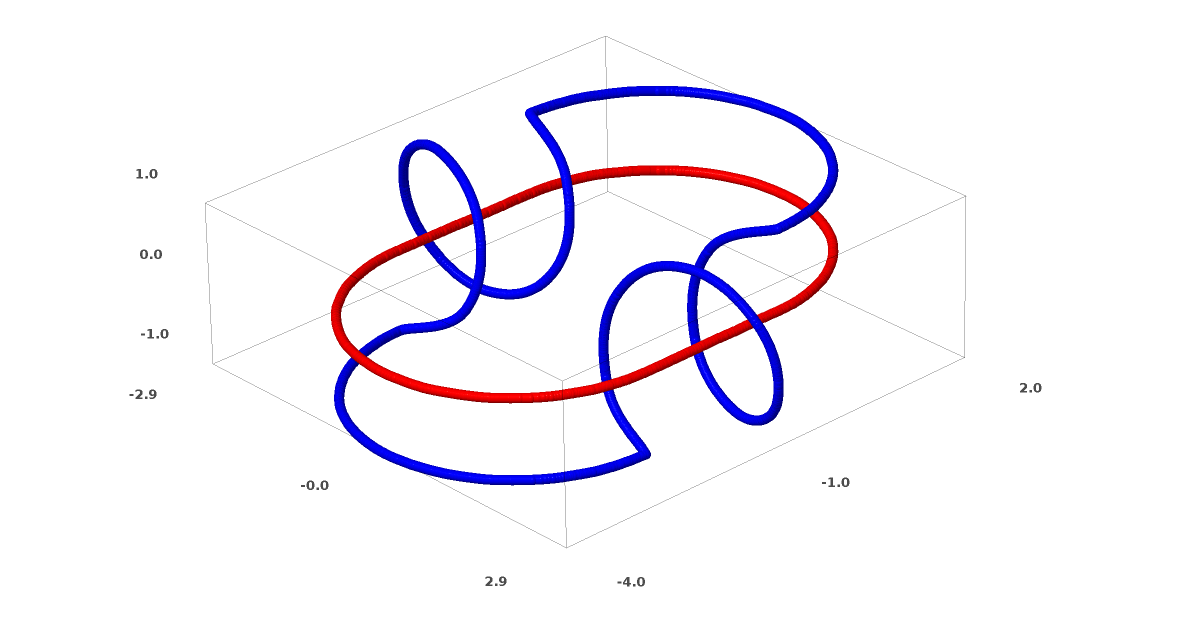
相对简单的不连贯。

如果仅使用具有三个单位的层的神经网络可以对其进行分类，则它是不连贯的。 （问题：从理论上讲，能否仅通过三个不一致性通过网络对所有不一致性进行分类？）

从该节点的角度来看，由神经网络创建的表示的连续可视化是解开连接的过程。 在拓扑中，我们将这种环境同位素称为原始链接和分离的链接之间的同位素。

形式上，变体A和B之间的周围空间的同位素是连续函数F：[0,1]×X→Y，这样每个Ft都是从X到其范围的同胚，F0是恒等函数，F1将A映射到B.T .e。 Ft连续从图A到自身，再到图A到B。

定理：如果以下情况，则入口与网络层表示之间存在周围空间的同位素：a）W不变性，b）我们准备将神经元转移到隐藏层，并且c）存在不止一个隐藏元素。


到目前为止，我们所说的关系不太可能出现在真实数据中，但存在更高层次的概括。 这些特征可能存在于真实数据中似乎是合理的。

连接和节点是一维流形，但是我们需要4维，以便网络可以解开所有维。 类似地，可能需要甚至更高尺寸的空间才能扩展n维歧管。 所有n维歧管均可扩展为2n + 2维。 [3]

轻松退出

最简单的方法是尝试将歧管拉开并拉伸尽可能缠结的零件。 尽管这将不会接近真正的解决方案，但是这种解决方案可以实现较高的分类精度，并且可以接受为局部最小值。



就解决拓扑问题而言，这样的局部最小值绝对是没有用的，但是拓扑问题可以为研究这些问题提供良好的动力。

另一方面，如果我们仅对获得良好的分类结果感兴趣，则该方法是可以接受的。 如果一小部分数据流形卡在另一个流形上，这是一个问题吗？ 尽管有这个问题，仍然有可能获得任意良好的分类结果。

用于操纵歧管的改进层？

很难想象具有仿射变换的标准层对于操纵流形确实非常有用。

也许有一个完全不同的层是有意义的，我们可以在更传统的层中使用它？

对矢量场进行研究的方向是我们希望的，可以改变流形：



然后根据矢量场对空间进行变形：



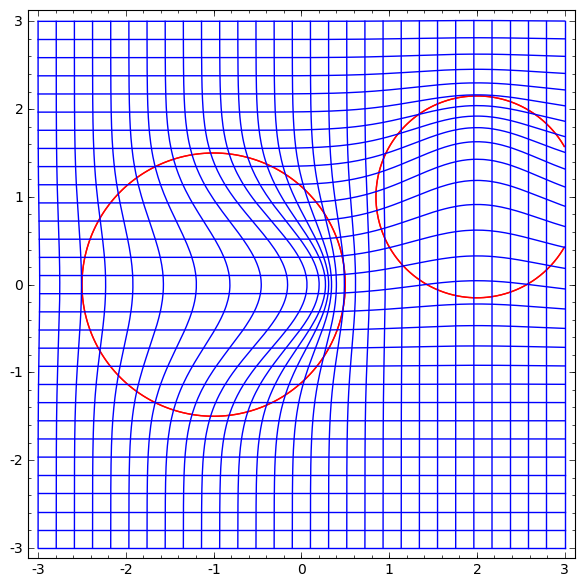
可以研究固定点处的矢量场（只需从测试数据集中获取一些固定点用作锚点）并以某种方式进行插值。


其中v0和v1是向量，而f0（x）和f1（x）是n维高斯。

K最近邻层

线性可分离性可能是神经网络的巨大需求，甚至可能是不合理的需求。 使用k最近邻（k-NN）方法是很自然的。 但是，k-NN的成功在很大程度上取决于其分类的表示形式，因此在k-NN可以正常工作之前，需要一个良好的表示形式。

k-NN在其作用的表示上是可区分的。 这样，我们可以直接训练网络对k-NN进行分类。 可以将其视为替代softmax的一种“最近邻居”层。
我们不想警告每个小型派对我们整个培训过程，因为这将是一个非常昂贵的过程。 适应的方法是基于小批量的其他元素的类别对小批量的每个元素进行分类，给出每个单位权重除以与分类目标的距离。

不幸的是，即使是复杂的体系结构，使用k-NN也会降低出错的可能性-而使用更简单的体系结构也会降低结果的准确性。

结论

数据的拓扑属性（例如关系）可能导致使用低维网络无法线性划分类，无论深度如何。 即使在技术上可行的情况下。 例如，螺旋线很难分开。

为了进行准确的数据分类，神经网络需要广泛的层次。 另外，神经网络的传统层不太适合用歧管来表示重要的操作。 即使我们手动设置权重，也很难紧凑地表示我们想要的转换。