小号公式和该算法的Python实现

而不是前言

不久前，在互联网上，我了解了巴比伦图书馆的精彩绝妙副本，如塔珀公式 。 相反，它更是特珀的不等式而不是公式。 这种不平等的独特之处在于它在图表上创建了自己的图像。 看看这个奇迹！



（维基百科来源）

您在图像中看到的是相同的Jeff Tupper的公式。 可能有一半的读者已经了解了这种不平等的结果……但这并不是那么简单。 如您在该图像中看到的，可以在沿OY [k; k + 15]。 这个神秘数字k是什么？ 在哪里得到的？ 事实是，根据巴比伦库的概念，这种不等式可以显示分辨率为106x17的任何图像！ 每个图像在图上都有其自己的位置，从而具有唯一的数字k。 因此， 对于每个数字k，整个图上只有一个图像 ！

对于给定的图像，数字k如下：

4858450636189713423582095962494202044581400587983244549483093085061934704708809928450644769865524364849997247024915119110411605739177407856919754326571855442057210445735883681829823754139634338225199452191651284348332905131193199953502413758765239264874613394906870130562295813219481113685339535565290850023875092856892694555974281546386510730049106723058933586052544096664351265349363643957125565695936815184334857605266940161251266951421550539554519153785457525756590740540157929001765967965480064427829131488548259914721248506352686630476300

看着将滚动到这样的坐标以查看公式的人很有趣

我想到用Python3编写一个程序，将图像转换为数字k，反之亦然，并告诉您将图像编码为数字的另一种好方法。

理论

（添加）如何工作？

让我们看一下公式本身：

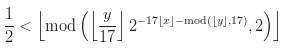
让我们定义其语法：
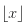
-数字四舍五入
mod（x，y）-x除以y的余数

然后，似乎一切都清楚了。
请注意，x和y均四舍五入。 正是这种舍入最终使我们获得了像素图像


表示不等式右边四舍五入的所有内容 $$$\ alpha$。
然后

$$

$$1/2 <[\ alpha] <=> 1 <= [\ alpha]$$

这很明显，因为整个表达式都是四舍五入的。

令y = 17r + q，其中r是y除以17的整数部分，r是除数的余数。 因此，我们可以将公式替换为 $$$[y / 17]$在r上 $$$mod（y，17）$在q。

我们得到

$$

$$1 <= mod（q * 2 ^ {-17-r}，2）$$

要不然

$$

$$1 <= mod（q / 2 ^ {17x + r}，2）$$

mod（ $$$\ alpha$，2）取2个值-0或1。因此，这个不等式将说明 $$$q / 2 ^ {17x + r}$甚至没有。

请注意，分别在间隔[N，N + 16]中查看图像 $$$q = [y / 17]$在整个图像高度上保持恒定，这无法说成是数r（整个图像的高度在0到16之间变化）。

现在是蛋糕上的樱桃。 编号 $$$[q / {2 ^ {17x + r}}]$当且仅当q的二进制表示形式的位数（17x + r）等于1时，奇数才是奇数。而且由于q随高度及其二进制表示形式也在不断变化，因此每次都能获得唯一的图像！ 这正是塔珀公式的原理。

现在，让我们看看如何计算想要看到图像的高度

计算数k的原理

特珀本人描述了任何106x17图像的k的计算（这很重要！），如下所示：

1. 将图像转换为黑白
2. 从下到上，从左到右读取每个像素，并将其放入缓冲区。 如果像素为黑色-如果是白色，则输入1-0。
3. 将二进制转换为十进制并乘以17
4. 赢利！

为了从数字k获得图像，我们要做的恰恰相反。 好吧，让我们开始编码！

科迪姆

UPD：在注释中，人们对代码进行了一些改进，使其更简单，更透明。 本文已发布更新数据。 如果您想查看代码的旧版本-转到github存储库（直到提交它，在文章结尾处链接）并在注释中

从k到图像

UPD

应评论员的要求， 添加了一种使用此不等式和k！来计算图像的新方法。 现在，我们将不使用数字进行操作，而是将其转移到二进制系统，而是直接影响函数本身！

使用Tapper方法解码数字k

我们从用户那里得到数字k， 闭上眼睛，我们将其除以17，然后将其转换为二进制系统。

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:] 

我们知道，对于我们的二进制数，一些初始像素可以分别为白色（等于0），第一位将为零，而当将数字转换为十进制时，这些初始零将丢失。 因此，我们检查生成的二进制数的大小，如果它小于1802，则在开头添加零。

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:] #   RadicalDreamer binary = ("0" * (1802 - len(binary))) + binary 

接下来，声明一个二维列表，我们将在其中存储有关图像每一行的信息。 然后我们记下所有读取的位（不要忘记创建数字k的算法-从下到上，从左到右）

 lists = [[] for x in range(17)] #C   RadicalDreamer for x in range(1802): lists[-(x % 17)].append(binary[x]) <b> !</b> <source lang="python"> #-----!-----# image = Image.new("1", (106,17), (0)) # -  10617 draw = image.load() for y in range(17): for x in range(106): image.putpixel(xy=(105-x,16-y), value=(int(lists[y][x]),)) #    ,      lists image.save("image.png") #  

让我们尝试将我在本文开头指出的数字k推入我们的程序并获得以下内容：



如您所见，一切都为我们解决了，现在我们可以解码任何k！

使用不等式从k生成图片

首先，在python中编写函数：

 def f(x,y): return ((y//17)//(1 << (17*x+(y%17))))%2 

借助//和<<操作符，大大简化了函数的实现。 确保数字x和y为整数 ！

我们再次创建一个二维列表，在其中存储图像的位并使用循环将有关每行的信息写入其中

 lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2)) 

然后，与前面的示例一样，我们使用PIL库绘制图片。

完整功能如下所示：

 def from_k_to_bin(k: int) -> list: lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2)) return lists 

图片以k

好了，现在我们将学习将任何图像编码为数字k。

首先我们得到图像本身

 def get_image() -> Image: name = input("   (      ):") try: im = Image.open(name) except Exception: print("!") exit(0) return im 

检查其大小

 _SIZE_WIDTH = 106 _SIZE_HEIGHT = 17 image = get_image() width, height = image.size flag_okay = False if width == _SIZE_WIDTH and height == _SIZE_HEIGHT: flag_okay = True if not flag_okay: print("  ") print(width, height) exit(0) print(" !") 

我们将图像设为黑白，然后开始逐像素读取：

 image = image.convert('1') byteset = "" for x in range(105,-1,-1): for y in range(0,17): #c m03r   if image.getpixel((x,y)) > 127: byteset += '1' else: byteset += '0' 

它仅保留转换为十进制并乘以17。

 k = int(byteset,2)*17 print(" :") print(k) 

好吧，我们去测试吧！

我决定为habr徽标编码。 这是源图像：



我们启动程序并指定图像名称：



我们得到以下k：

4858487703217654168507377107565676789145697178497253677539145555247620343537955749299116772611982962556356527603203744742682135448820545638134012705381689785851604674225344958377377969928942310236199337805399065932982909660659786056259547094494380793146587709009524498386724160055692719747815828234655968636671461350354316223620304956111171025410498514602810746287134775641383930152393933036921599511277388743068766568352667661462097979110006690900253037600818522726237351439443865433159187625289316917268254866954663750093103703327097252478959

让我们在我们自己的程序上检查一下。

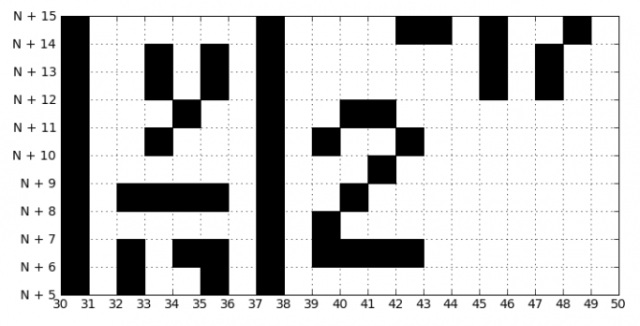
这是我们收到的图像：



由于黑白图像的翻译有些歪斜，因此有点失真。

总结

源代码： Github

资料来源： 维基文章