向所有人,尤其是对离散数学和图论感兴趣的人致以问候。
背景知识
碰巧的是,在兴趣的驱使下,我正在开发旅游建设服务。 路线。 任务是根据用户感兴趣的城市,场所类别和时间范围来规划最佳路线。 嗯,子任务之一是计算从一所机构到另一所机构的旅行时间。 由于我很小又很笨,所以我用Dijkstra的算法解决了这个问题,但公平地讲,值得注意的是,只有这样,才有可能从一个节点开始迭代到成千上万个其他节点,缓存这些距离不是一种选择,而在10k以上的场所单单莫斯科,以及诸如我们城市中曼哈顿距离之类的决策根本就没有用。
这样就可以解决组合问题中的性能问题,但是处理请求的大部分时间都花在了搜索非缓存路径上。 莫斯科的Osm路线图非常大(一半节点为100万,弧线为110万),这使问题变得复杂。
我不会谈论所有尝试,实际上可以通过切断图表的额外弧线来解决问题,我只是告诉您,在某个时候它突然出现在我身上,我意识到,如果您从概率方法的角度出发,采用Dijkstra的算法,它可以是线性的。
Dijkstra为对数时间
每个人都知道,但谁也知道,请读 Dijkstra的算法,即使用对数复杂度为插入和删除的队列可以导致复杂度为O(n log(n)+ m log(n))。 使用斐波那契堆时,复杂度可以降低到O(n * log(n)+ m),但仍然不是线性的,但是我想这样做。
在一般情况下,队列算法描述如下:
让:
- V是图顶点的集合
- E是图的边集
- w [i,j]是从节点i到节点j的边的权重
- a-搜索的起始顶点
- q-顶点队列
- d [i]-到第i个节点的距离
- d [a] = 0,对于所有其他d [i] = + inf
当q不为空时:
- v是最小d [v]为q的顶点
- 对于所有从顶点v过渡到E的顶点u
- 如果d [u]> w [vu] + d [v]
- 从q移除d,距离为[u]
- d [u] = w [vu] + d [v]
- 将u添加到q,距离d [u]
- 从q移除v
如果我们使用一棵红黑树作为队列,其中插入和删除在log(n)中发生,并且对最小元素的搜索在log(n)中相似,则该算法的复杂度为O(n log(n)+ m log(n)) 。
这里值得一提的一个重要特征:理论上,没有什么可以阻止多次考虑最高排名。 如果已经检查了顶点,并且到顶点的距离已更新为不正确的值,大于真实值,那么,只要系统早晚收敛,并且到u的距离更新为正确的值,就可以进行此类操作。 但值得注意的是-一个顶点应以低概率被考虑超过1次。
排序哈希表
为了将Dijkstra算法的运行时间缩短为线性算法,提出了一种数据结构,该数据结构是一个以节点号(node_id)为值的哈希表。 我注意到对d数组的需求并没有消失,仍然需要不断地获取到第i个节点的距离。
下图显示了所建议结构的示例。
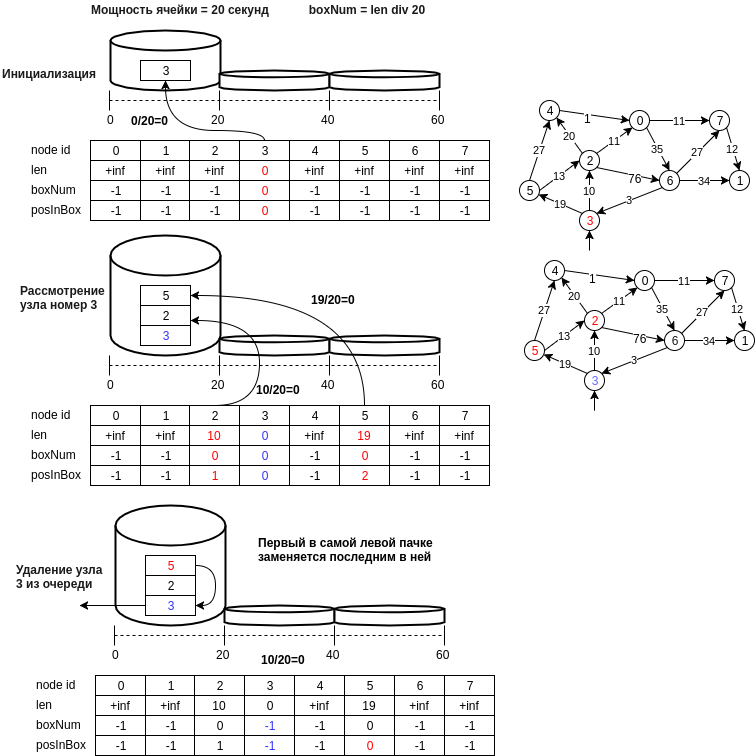
让我们分步描述建议的数据结构:
- 将节点u写入一个等于d [u] // bucket_size的数字的单元格中,其中bucket_size是该单元格的功率(例如20米,即编号为0的单元格将包含其距离将在[0,20]米范围内的节点) )
- 第一个非空单元格的最后一个节点,即 提取最小元素的操作将在O(1)中执行。 有必要保持第一非空单元格编号(min_el)的标识符的当前状态。
- 通过将新的节点号添加到单元的末尾并同时执行O(1)来执行插入操作,因为 单元数的计算是在固定时间内进行的。
- 像散列表的情况一样,可以执行删除操作,可以进行正常的枚举,并且可以做一个假设,并说单元格较小时,它也是O(1)。 如果您不介意内存(从原则上讲,不需要太多,n乘以另一个数组),则可以在单元格中创建一个位置数组。 在这种情况下,如果元素在单元格的中间被删除,则必须将单元格中的最后一个值移动到删除的位置。
- 选择最小元素时的重要一点:最小元素只有在一定的可能性下才是最小的,但是算法会一直看min_el单元,直到它变空为止,迟早会考虑真正的最小元素,并且如果我们不小心将距节点可达到的距离值更新为最小值,则与最小值相邻的节点可以再次位于队列中,并且到它们的距离将是正确的,依此类推。
- 您还可以删除不超过min_el的空单元格,从而节省内存。 在这种情况下,仅在考虑所有相邻节点之后才能从队列q中删除节点v。
- 并且还可以更改单元格功率,用于增加单元格大小的参数以及需要增加哈希表大小时的单元格数。
测量结果
检查是在莫斯科的osm地图上进行的,通过postgres中的osm2po卸载,然后加载到内存中。 测试是用Java编写的。 该图有3个版本:
- 源图-43万个节点,114万个弧
- 具有173k节点和750k弧的图形的压缩版本
- 图的压缩版本的行人版本,450k弧,100k节点。
以下是在不同版本的图表上进行测量的图片:

考虑重新查看顶点的概率与图形大小的相关性:
| 节点视图数 | 计数顶点 | 重新查看节点的概率 |
|---|
| 104915 | 100015 | 4.8 |
| 169429 | 167892 | 0.9 |
| 431490 | 419594 | 2.8 |
您可能会注意到,概率不取决于图形的大小,而是特定于请求的,但是它很小,并且其范围是通过更改单元格功率来配置的。 我非常感谢您为该算法的概率修改提供帮助,这些参数的参数保证了置信区间,在该区间内重复查看的概率不会超过一定百分比。
还进行了定性测量,以实际确认算法结果与新数据结构的正确性比较,该新结构显示了从1000个随机节点到1000个其他随机节点的最短路径长度的完全一致。 (以此类推250次迭代)在使用排序哈希表和红黑树时。
建议的数据结构的源代码位于链接上
PS:我了解Torup算法及其在线性时间内解决相同问题的事实,但是尽管我从总体上理解了这一想法,但我无法在一晚上掌握这项基本工作。 至少,据我了解,在那里提出了另一种方法,基于构建最小生成树。
PSS在一周之内,我将尝试找出时间并与Fibonacci一堆进行比较,稍后再添加带有示例和测试代码的github萝卜。