😙 🌭 🙎 在MATLAB中使用傅立叶变换计算信号反应的示例 👩🏻‍🎓 🦈 📟

当解决通过频率特性表示的线路的数据传输问题时，将应用傅立叶变换-信号从时域到频域的传输，反之亦然。 MATLAB环境具有解决此类问题的全套功能。在这项工作中，分析了一个在MATLAB中计算通过线路传输的信号的反应的示例，该线路的特性是在与数据传输频率不一致的频率下测量的。我希望该示例将使理解MATLAB环境中信号转换技术的功能更加容易。

任务条件

必须确定通过滤波器和信号线的二进制数字信号的形状变化。信号由振幅和传输速率设置。归一化为数据传输频率的二阶滤波器由时间常数设置。信号线的传递函数由实测频率响应以复数形式表示。

用于计算和显示数据的环境是MATLAB R2015a。
以下是在网站www.StatEye.org上发布的有关StatEye 3.0 GUI方法[1、2、3]版本的关系，这些数据作为初始数据的示例。

数据速率bps = 10.3125 Gbit / s 归一化二阶滤波器的时间常数是相同的；它们的倒数是数据传输频率的3/4。信号线由频率响应表示。该特性是在channel.f = 0.006495：0.0012475：20 GHz处测得的。指定数量的傅里叶变换采样点：点= 2 ^ 13。

图1显示了本文讨论的数据传输，序列和数据处理结果。使用快速傅里叶变换（FFT）算法执行从时域到频域的转换，反之亦然。

图1.数据通道。 输入信号iSignal.Tx，滤波器iSignal.Filter_out的输出信号，输出信号线iSignal.Rx。 该图所示的特性将在下面讨论。

计算顺序

在这项工作中，主要计算是在频域中进行的。为此，使用傅立叶变换将来自时域的原始信号传输到频域，方法是将信号，滤波器和信号线的频谱特性相乘，找到路径的输出信号，然后通过傅立叶逆变换将信号从频域传输到时域。

数据传输速率是数据传输频率的两倍。被测信号线的最大频率最大值（channel.f）= 20 GHz。在此频率下，数据可以40 Gbit / s的速度传输（最大2 *（channel.f））。

最大数据传输速率不超过信号线上的最大传输速率40 Gbit / s和bps = 10.3125 Gbit / s的倍数传输速率，为fmax = 30.9375 Gbit / s，多重性N = 3（N = fmax / bps）。此外，fmax用作使用傅里叶变换计算信号响应的极限频率。

将输入信号转换到频域

用于在时域Ts = 1 / fmax中构建输入信号（数据位）的时间离散性； Ts ＝ 3.232e-11s。关于信号持续时间进行归一化，时间标度由2 ^ 13个点（点）组成，该标度包括以下点阵列：时间= bps / Ts。*（1：点）。传输速率为bps = 10.3125 Gbit / s且周期为Ts = 1 / fmax的离散单个信号由三个点组成，这些点的归一化时间为10到11个单位。可以在时间轴上的任何其他位置构建单位幅度的信号，但最好从边缘后退以完全看到背景和输出信号的过渡过程。使用以下MATLAB命令构造的脉冲信号（数据位）如图2所示。

iSignal.Tx(1:size(time,2)) = 0; t0 = max(find(time<=10)); t1 = max(find(time<11)); iSignal.Tx(t0:t1) = 1.0;

图2.输入脉冲信号iSignal.Tx，数据位。

通过以下FFT功能将iSignal.Tx信号转换到频域。

 iSignal.shiftedPSD = fft(iSignal.Tx); iSignal.PSD = fftshift(iSignal.shiftedPSD);

傅立叶变换函数fft在正和负频率区域中构造信号的对称频谱，该信号的最大频率位于频谱的中心（请参见图3）。 fftshift功能通过将信号的零频率偏移到中心来恢复频谱，如图4所示。

频谱频率的分辨率为fs = fmax /点；频谱频率范围从-fmax / 2到fmax / 2-fs，等于f = -fmax / 2：fs：fmax / 2-fs；

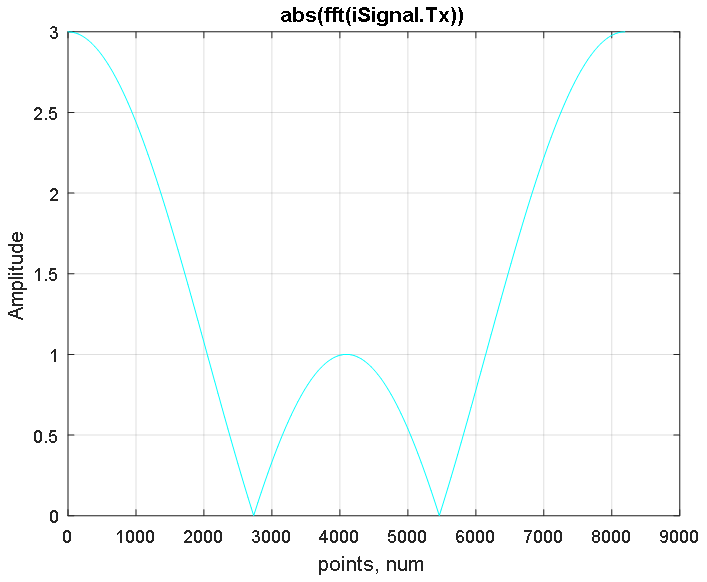图3.使用FFT获得的iSignal.Tx信号移位频谱的幅度响应。

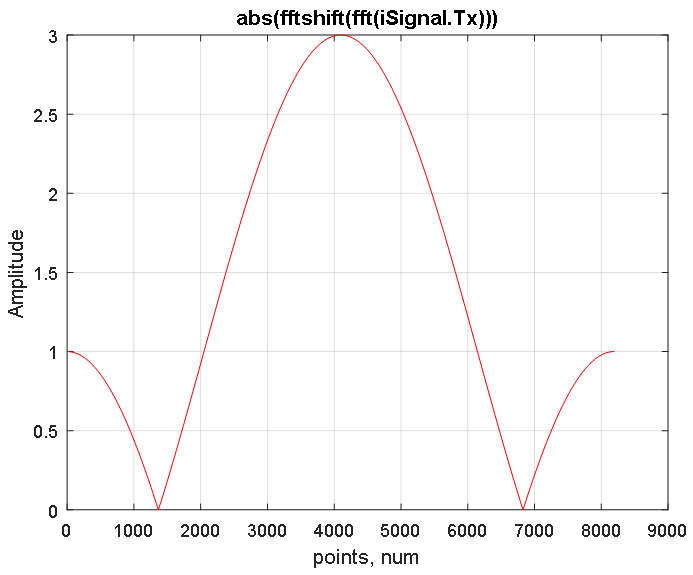图4. iSignal.Tx信号重构频谱的幅度响应如图3所示。给出了2 ^ 13个样本。 4097处的平均计数对应于零频率。 负频率位于左侧（从1到4096点），正频率区域位于右侧（从4098到8192点）。

归一化低通滤波器的传递函数

在此示例中，二阶滤波器的传递函数具有以下形式

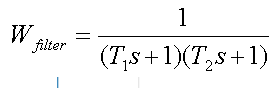
其中T1和T2是滤波器时间常数。相对于数据传输的频率，频率1 / T1相等，并且设置1 / T2：1 / T1 = 1 / T2 = 0.75 * bps（bps = 10.3125 Gbit / s）。

归一化滤波器带宽

 f_nrm =fmax/bps/points.*(-points/2:points/2-1).

操作员

 s = f_nrm .* j;

相对于信号传输频率进行归一化的正负频率归一化滤波器的幅度相位特性如图5所示。滤波器的对数幅度频率特性如图6所示。

图5.归一化滤波器的幅度相位特性

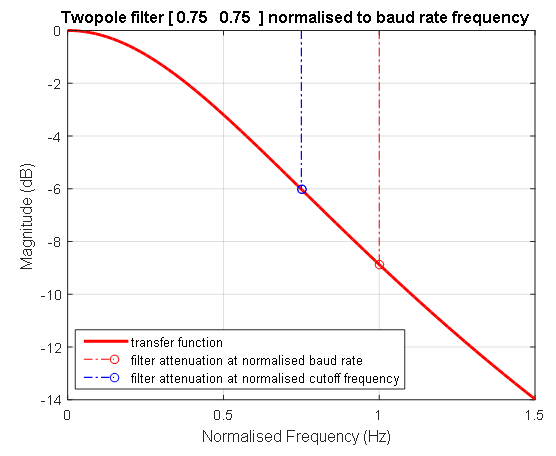图6.归一化滤波器的对数幅度-相位频率响应。 蓝色虚线表示滤波器频率的位置，其值为数据传输频率的0.75。 在此频率（1 / T1 / = 1 / T2）下，二阶滤波器的传输系数为-6分贝。 红色虚线表示正在传输数据的单位频率。

将信号线测量结果转换为传递函数的类型

测得的信号线幅度相位特性包括在高达20 GHz的频带中以固定的12.475 MHz步进的1599个采样。它包含以下频率值：channel.f = 0.006495：0.0012475：20 GHz。最初，信号线由四端子特性表示。该特性已被转换，并在示例中用作一维复数函数。

测量结果获得的信号线特征频率与输入信号频谱的频率不一致，后者是数据传输频率的倍数。另外，信号线频谱仅包含正频率，不包含零区域中的频率。输入信号频谱包含正，零和负频率。
要将信号线的特性转换为传递函数（即频率与输入信号频谱频率一致的特性），请执行以下步骤。

1.通过外推法计算零频率时线路特性的幅度。为此，从最接近零频率的幅度特性的十个点中，找到近似于幅度特性的线性多项式系数：

 [a] = polyfit(channel.f(1:10), channel.abs(1:10), 1);

找到的第二个多项式系数等于零频率处的特性幅度：

 channel.dc = a(2);

2.零频率下的相位响应等于零。

 channel.dcPhase = 0.00;

3.对输入信号频谱的频率（f = -fmax / 2：fmax /点：fmax / 2-fmax /点）执行具有零频率值的信号线幅度通道.abs和相位channel.phase特性的重新计算。零频率和负频率区域：

 ichannel.abs = interp1([0 channel.f], [channel.dc channel.abs], abs(f), 'linear', 'extrap'); ichannel.phase = interp1([0 channel.f], [channel.dcPhase unwrap(channel.phase)], abs(f), 'linear', 'extrap'); ichannel.s = ichannel.abs .* exp(+j.*ichannel.phase); ichannel.tf = real(ichannel.s) + j*imag(ichannel.s) .* sign(f);

所获得的传递函数-低频区域中通道的幅度-相位频率响应如图7所示。测量信号线的幅度-频率特性和整个频率范围内计算出的传递函数如图8所示。相空间中的相同特性如图9所示。

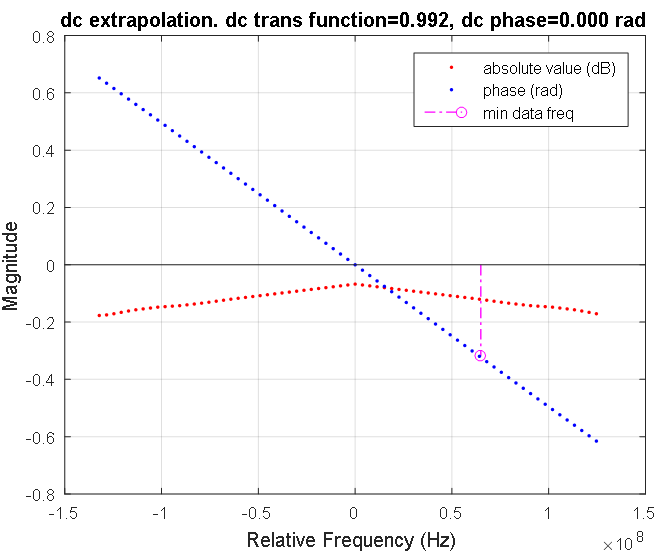图7.低频区域中信号线的传递函数。 红点和蓝点分别表示离散的幅度和相位特性。 幅度响应以分贝表示，相位以弧度表示。 粉色线表示信号线的测量特性的最低频率。 零频率下的传输系数为0.992。

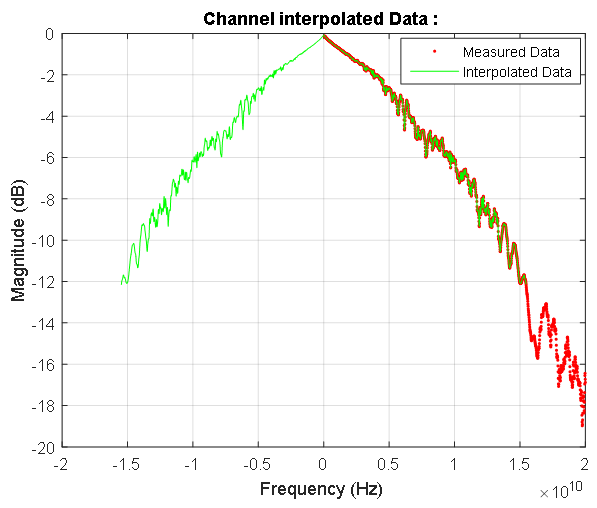图8.信号线的频率响应。 蓝点表示被测线的复杂数据。 计算出的信号线增益在输入信号频谱频率处的对称相关性以红色突出显示。 在零频率区域，该特性如图7所示。

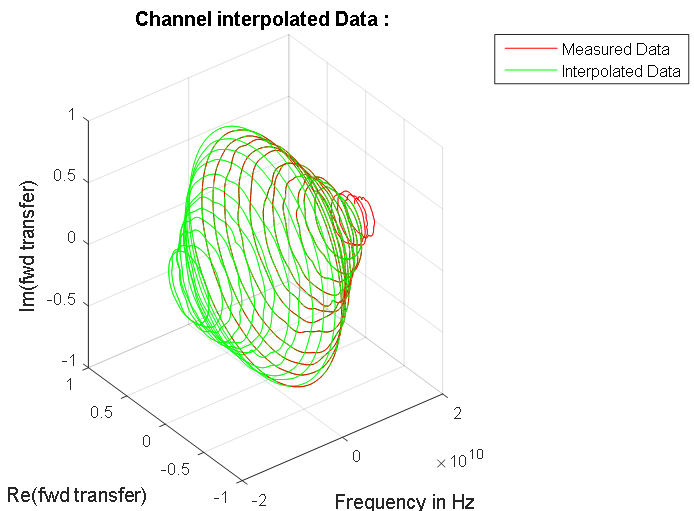图9.被测数据线及其归一化频谱的幅相频率特性。

信号响应计算

通过将信号频谱乘以使反应与输入信号相关的元素的传递函数乘积，可以得到频域中的响应（对输入效果的响应）。在我们的情况下，信号通过滤波器和信号线。
傅立叶逆变换ifft用于将信号从频域传输到时域。

iSignal.Filter_out时域中的过滤器输出计算为

 TransFunction.PSD = iSignal.PSD .* Filter.PSD_Tx; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Filter_out = real(ifft(TransFunction.shiftedPSD));

iSignal.Rx线的输出信号等于输入信号的频谱与滤波器和信号线的传递函数以及接收信号随后从频域到时域的传递的乘积。

 TransFunction.PSD = TransFunction.PSD .* ichannel.tf; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Rx = real(ifft(TransFunction.shiftedPSD));

滤波器对输入理想脉冲的响应和通道的响应如图10所示。

图10.滤波器输出（红色图）和数据线输出（绿色图）。 滤波器输入信号-单脉冲如图2所示。信号线输入是滤波器输出信号。

应用程序。二手m代码MATLAB

上市

 clear all %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Ini data %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% bps = 1.03125e+10; FilterParam = [0.75 0.75]; points = 2^13; load('channel'); N = floor(max(channel.f)*2/bps); fmax = N*bps; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Signal %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % normalise all the scales for the bit rate time = bps/fmax .* (1:points); iSignal.Tx(1:size(time,2)) = 0; t0 = max(find(time<=10)); t1 = max(find(time<11)); iSignal.Tx(t0:t1) = 1.0; figure plot(time(1:t1+10), iSignal.Tx(1:t1+10),'b'); hold on plot(time(1:t1+10), iSignal.Tx(1:t1+10),'xb'); grid on xlabel('Normalised Time, tick Ts = 1/fmax'); ylabel('Normalised Amplitude'); title(['Pulse, data bit']); iSignal.shiftedPSD = fft(iSignal.Tx); figure plot(abs(iSignal.shiftedPSD),'c'); grid on xlabel('points, num'); ylabel('Amplitude'); title(['abs(fft(iSignal.Tx))']); iSignal.PSD = fftshift(iSignal.shiftedPSD); figure plot(abs(iSignal.PSD),'r'); grid on xlabel('points, num'); ylabel('Amplitude'); title(['abs(fftshift(fft(iSignal.Tx)))']); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Filter %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% f_nrm =fmax/bps/points.*(-points/2:points/2-1); s = f_nrm .* j; Filter_PSD = 1 ./(1 + s/FilterParam(1)) ./ (1 + s/FilterParam(2)); figure [AX,H1,H2] = plotyy (f_nrm, abs(Filter_PSD), f_nrm, phase(Filter_PSD)); hold(AX(1)); hold(AX(2)); set(H1,'LineWidth',2); grid(AX(2),'on'); xlabel('Normalised Frequency (Hz)'); set(get(AX(1),'Ylabel'),'String','Gain'); set(get(AX(2),'Ylabel'),'String','Phase, rad'); title(['Twopole filter [' sprintf(' %3.2f ', FilterParam) '] normalised to baud rate frequency']); figure plot_handles_Filter = plot(f_nrm(points/2 + 1:points), 20*log10(abs(Filter_PSD(points/2 + 1:points))), 'r', 'linewidth', 2); hold on stem_handles_br = stem(1, 20*log10(abs(Filter_PSD(max(find(f_nrm < 1))))), '-.ro'); hold on stem_handles_c = stem(FilterParam, [20*log10(abs(Filter_PSD(max(find(f_nrm < FilterParam(1)))))) 20*log10(abs(Filter_PSD(max(find(f_nrm < FilterParam(2))))))], '-.bo'); grid legend_handles = [plot_handles_Filter, stem_handles_br(1), stem_handles_c(1)]; legend(legend_handles, 'transfer function', 'filter attenuation at normalised baud rate', 'filter attenuation at normalised cutoff frequency', 3); xlabel('Normalised Frequency (Hz)'); ylabel('Magnitude (dB)'); title(['Twopole filter [' sprintf(' %3.2f ', FilterParam) '] normalised to baud rate frequency']); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Channel %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % create negative frequencies, convert data to complex value, taking care about negative frequency channel.abs = abs(channel.s); channel.phase = angle(channel.s); %channel.s = channel.abs .* exp(+j.*channel.phase); [a] = polyfit(channel.f(1:10), channel.abs(1:10), 1); channel.dc = a(2); channel.dcPhase = 0.00; fs = fmax/points; % frequency step f = -fmax/2:fs:fmax/2-fs; % frequency matrix % create new data structure with linearly interpolated data ichannel.abs = interp1([0 channel.f], [channel.dc channel.abs], abs(f), 'linear', 'extrap'); ichannel.phase = interp1([0 channel.f], [channel.dcPhase unwrap(channel.phase)], abs(f), 'linear', 'extrap'); % correct for negative frequencies ichannel.s = ichannel.abs .* exp(+j.*ichannel.phase); ichannel.tf = real(ichannel.s) + j*imag(ichannel.s) .* sign(f); figure disp_points = 2*round(channel.f(1)/fs); stem_handles_br = stem(channel.f(1), angle(ichannel.tf(max(find(f < channel.f(1))))), '-.mo'); hold on plot_abs = plot(f(points/2-disp_points:points/2+disp_points), 20*log10(abs(ichannel.tf(points/2-disp_points:points/2+disp_points))), '.r', 'linewidth', 3); hold on plot_phase = plot(f(points/2-disp_points:points/2+disp_points), angle(ichannel.tf(points/2-disp_points:points/2+disp_points)), '.b', 'linewidth', 3); grid legend_handles = [plot_abs, plot_phase, stem_handles_br(1)]; legend(legend_handles, 'absolute value (dB)', 'phase (rad)', 'min data freq', 3); xlabel('Relative Frequency (Hz)'); ylabel('Magnitude'); title(sprintf('dc extrapolation. dc trans function=%4.3f, dc phase=%4.3f rad', abs(ichannel.tf(points/2+1)), angle(ichannel.tf(points/2+1)))); figure plot(channel.f, 20*log10(channel.abs), '.r', 'linewidth', 3); hold on plot(f, 20*log10(ichannel.abs), 'g'); grid on legend('Measured Data', 'Interpolated Data', 3); xlabel('Frequency (Hz)'); ylabel('Magnitude (dB)'); title(['Chnnel interpolated Data : ']); figure plot3(channel.f, real(channel.s), imag(channel.s),'r'); hold on plot3(f, real(ichannel.tf), imag(ichannel.tf),'g'); grid on legend('Measured Data', 'Interpolated Data'); xlabel('Frequency in Hz'); ylabel('Re(fwd transfer)'); zlabel('Im(fwd transfer)'); title(['Chnnel interpolated Data : ']); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Response %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % filter Output TransFunction.PSD = iSignal.PSD .* Filter_PSD; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Filter_out = real(ifft(TransFunction.shiftedPSD)); % pass through channel TransFunction.PSD = TransFunction.PSD .* ichannel.tf; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Rx = real(ifft(TransFunction.shiftedPSD)); figure plot(time, iSignal.Filter_out,'r'); hold on [max_Tx, time_maxTx] = max(iSignal.Filter_out); [min_Tx, time_minTx] = min(iSignal.Filter_out); [max_Rx, time_maxRx] = max(iSignal.Rx); dtime_p5= round((time_maxRx - time_maxTx)*time(1) -1); plot(time - dtime_p5, iSignal.Rx,'g'); hold on plot(time, iSignal.Filter_out,'rx'); axis([(time_maxTx*time(1) - 3) (time_maxTx*time(1) + 5) (min_Tx-0.15) (max_Tx+0.1)]) grid on legend('Filter out','Rx', 2); xlabel('Normalised Time'); ylabel('Normalised Amplitude'); title(sprintf('Transmit pulse (Tx) max= %4.3f; Response (Rx) max (h0)= %4.3f', max(iSignal.Filter_out), max(iSignal.Rx)));

书目清单

1. IEEE802.3ap。在级联通道组件上使用“ StatEye”和“信号到干扰模型”进行的10.3125Gbps NRZ仿真结果。 Shannon Sawyer和Charles Moore /安捷伦科技公司。 2005年1月24日www.ieee802.org/3/ap/public/jan05/sawyer_01_0105.pdf

2.什么是StatEye。 IEEE 803.3ap工作队。 2004年9月16日www.ieee802.org/3/ap/public/signal_adhoc/ghiasi_01_0904.pdf

3. Stat Eye / IBM协议。史蒂夫·安德森。 Xilinx，Inc. www.ieee802.org/3/ap/public/nov04/anderson_01_1104.pdf

在MATLAB中使用傅立叶变换计算信号反应的示例