“本课程的目标是为您的技术未来做好准备。”
哈Ha 还记得很棒的文章
“您和您的工作” （+219、2442个书签，394k读取）吗？
因此，汉明（是的，是的，自我检查和自我纠正的
汉明代码 ）根据他的演讲编写了一整
本书 。 我们正在翻译它，因为那个人在谈论生意。
这本书不仅是关于IT的书，还是关于令人难以置信的酷人的思维方式的书。
“这不仅仅是积极思考的冲动； 它描述了增加做出色工作机会的条件。”我们已经翻译了30章中的28章。
我们正在纸上版。
编码理论-I
在考虑了计算机及其工作原理之后，我们现在将考虑信息问题：计算机如何表示我们要处理的信息。 任何字符的含义可能取决于其处理方式，机器对于所使用的位没有特定的含义。 在讨论软件历史时，第4章讨论了一种综合编程语言，其中break指令的代码与其他指令的代码一致。 对于大多数语言来说，这种情况是典型的，指令的含义由相应的程序确定。
为了简化呈现信息的问题，我们考虑了从点到点传输信息的问题。 这个问题与保护信息的问题有关。 在时间和空间上传输信息的问题是相同的。 图10.1显示了用于传输信息的标准模型。
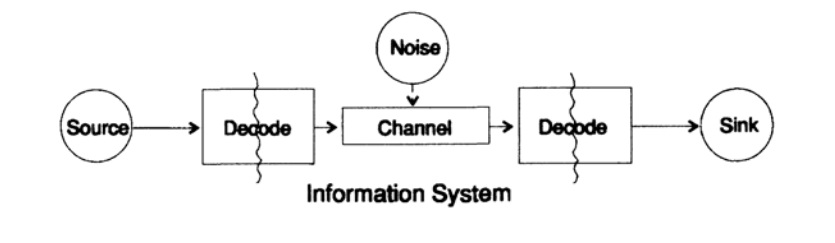图10.1信息源位于图10.1的左侧。 在考虑模型时，我们不在乎来源的性质。 它可以是一组字母符号，数字，数学公式，音符，可以用来代表舞蹈动作的符号-来源的性质和其中存储的符号的含义不属于传输模型的一部分。 我们仅考虑信息源，在这种限制下，我们获得了可以扩展到许多领域的强大而通用的理论。 它是来自许多应用程序的抽象。
当香农在1940年代末创建信息论时，人们认为应该将其称为传播理论，但他坚持使用信息一词。 这个术语已成为引起人们越来越多的兴趣和理论上不断失望的一个持续原因。 研究人员希望建立完整的“信息理论”，然后退化为一组字符理论。 回到传输模型，我们有一个数据源需要进行编码以进行传输。
编码器由两部分组成，第一部分称为源编码器，确切名称取决于源类型。 不同类型数据的源对应于不同类型的编码器。
编码过程的第二部分称为通道编码，取决于传输数据的通道类型。 因此，编码过程的第二部分与传输信道的类型一致。 因此，当使用标准接口时，来自源的数据首先根据接口的要求进行编码，然后根据所用数据通道的要求进行编码。
根据该模型，在图10.1中，数据通道暴露于“其他随机噪声”。 此时，系统中的所有噪声都已合并。 假定编码器接受所有字符而没有失真，并且解码器执行其功能而没有错误。 这是一种理想化，但出于许多实际目的，它已接近现实。
解码阶段还包括两个阶段：信道-标准，标准-数据接收器。 在数据传输结束时，将数据传输给使用者。 同样，我们没有考虑消费者如何解释这些数据。
如前所述，数据传输系统，例如电话消息，广播，电视节目，在计算机的寄存器中以一组数字的形式显示数据。 我再说一遍，空间传输与时间传输或存储信息没有什么不同。 您是否有一段时间需要的信息，然后必须对其进行编码并将其存储在数据存储源上。 如有必要，对信息进行解码。 如果编解码系统相同，我们将通过传输通道传输数据而不会发生变化。
所提出的理论与物理学中通常的理论之间的根本区别是假设源和接收器中没有噪声。 实际上，任何设备都会发生错误。 在量子力学中，噪声是根据不确定性原理在任何阶段发生的，而不是初始条件。 无论如何，信息论中的噪声概念并不等同于量子力学中的类似概念。
为了确定性，我们将进一步考虑系统中数据表示的二进制形式。 其他形式的处理方式相似，为简单起见，我们将不考虑它们。
我们开始考虑具有可变长度编码字符的系统，如点和破折号的经典摩尔斯电码一样，其中频繁出现的字符较短，而稀有字符较长。 这种方法可以提高代码效率，但是值得注意的是，莫尔斯电码是三进制的，而不是二进制的，因为它在点和破折号之间包含一个空格。 如果代码中的所有字符都具有相同的长度，则将这样的代码称为分组代码。
代码的第一个显而易见的必要属性是在没有噪声的情况下唯一解码消息的能力，至少这似乎是期望的属性，尽管在某些情况下可以忽略此要求。 来自接收器的传输通道的数据看起来像是从零到一的字符流。
我们将两个相邻字符称为双扩展名，将三个相邻字符称为三重扩展名，在通常情况下，如果转发N个字符，则接收者会看到N个字符的基本代码有增加。 接收器不知道N的值，必须将流分成广播块。 或者，换句话说，接收方应该能够唯一地分解流，以便恢复原始消息。
考虑由少量字符组成的字母，通常字母要大得多。 语言字母从16到36个字符开始，包括大写和小写字母，数字符号，标点符号。 例如，在ASCII表中128 = 2 ^ 7个字符。
考虑由4个字符s1，s2，s3，s4组成的特殊代码
s1 = 0; s2 = 00； s3 = 01; s4 = 11。接收方应如何解释下一个接收到的表达式
0011？s1s1s4或
s2s4如何？
您不能对这个问题给出明确的答案，因为此代码绝对不会解码，因此效果不理想。 另一方面，代码
s1 = 0; s2 = 10； s3 = 110； s4 = 111以独特的方式解码消息。 取一个任意字符串，并考虑接收方将如何对其进行解码。 您需要根据图10.II中的表格构建一个解码树。 弦乐
1101000010011011100010100110 ...
可以分成字符块
110，10，0，10，0，110，111，0，0，0，10，10，0，110， ...
根据以下规则来构建解码树：
如果您在树的顶部，请阅读下一个字符。 当您到达树上的叶子时，可以将序列转换为字符，然后返回起点。
之所以存在这样的树，是因为没有字符是另一个树的前缀，因此您始终知道何时需要返回到解码树的开头。
有必要注意以下几点。 首先，解码是严格的流过程，其中每个位仅被检查一次。 其次，协议通常包括字符，这些字符是解码过程结束的标记，并且是指示消息结束的必要字符。
未能使用结尾字符是代码设计中的常见错误。 当然，您可以提供恒定的解码模式，在这种情况下，不需要尾随字符。
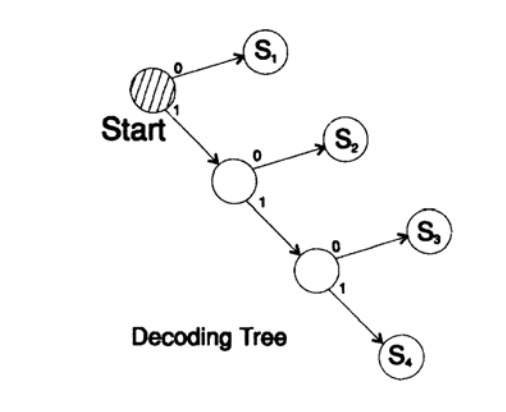图10.II下一个问题是用于流（即时）解码的代码。 考虑通过显示字符从上一个代码获得的代码
s1 = 0; s2 = 01; s3 = 011; s4 = 111。假设我们得到序列
011111 ... 111 。 解码消息文本的唯一方法是将3末尾的位分组为一个组，然后选择前一个前导零的组，然后再进行解码。 这样的代码以独特的方式解码，但不是立即解码！ 要进行解码，您必须等待传输结束！ 在实践中，这种方法消除了解码速率（麦克米伦定理），因此，有必要寻找即时解码的方法。
考虑两种编码相同字符Si的方法：
s1 = 0; s2 = 10； s3 = 110； s4 = 1110，s5 = 1111，这种方法的解码树如图10.III所示。
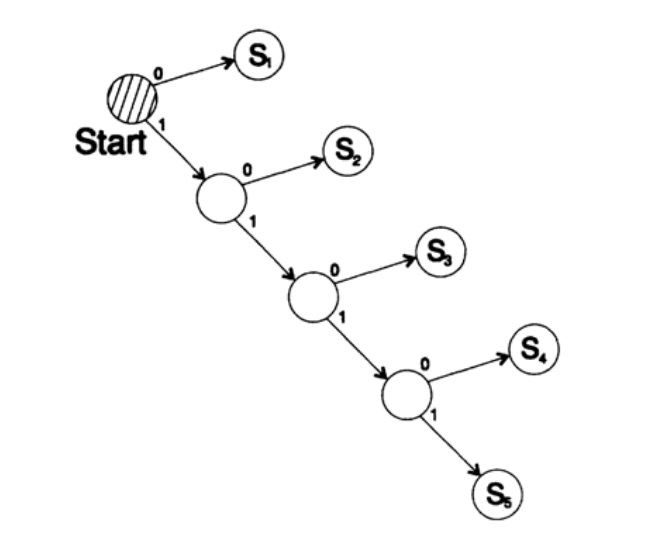图10.III第二种方式
s1 = 00； s2 = 01; s3 = 100； s4 = 110，s5 = 111 ，
这种关心的解码树如图10.IV所示。
衡量代码质量的最明显方法是一组消息的平均长度。 为此，必须计算每个字符的代码长度乘以相应的pi出现概率。 因此，获得了整个代码的长度。 q个字符的字母的代码的平均长度L的公式如下
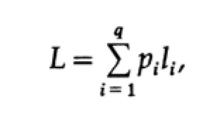
其中pi是符号si出现的概率，li是编码符号的相应长度。 为了获得有效的代码，L的值应尽可能小。 如果P1 = 1/2，p2 = 1/4，p3 = 1/8，p4 = 1/16和p5 = 1/16，则对于代码1，我们得到代码长度值
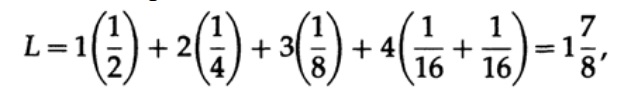
对于代码2
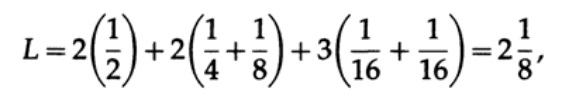
获得的值表示第一个代码的优先级。
如果字母表中的所有单词都具有相同的出现概率，则第二个代码将更可取。 例如，对于pi = 1/5，代码长度为1
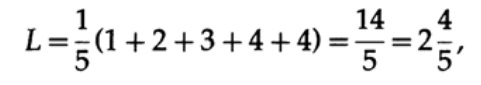
和代码长度＃2
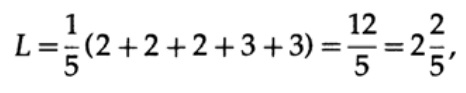
此结果显示了对2个代码的偏好。 因此，开发“好”代码时，必须考虑出现字符的可能性。
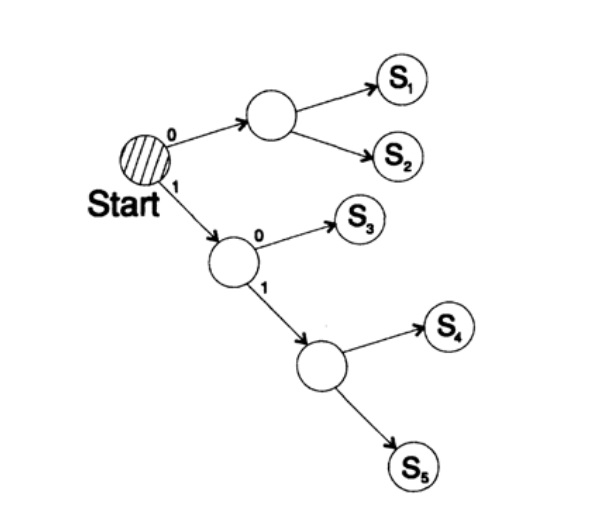图10.IV
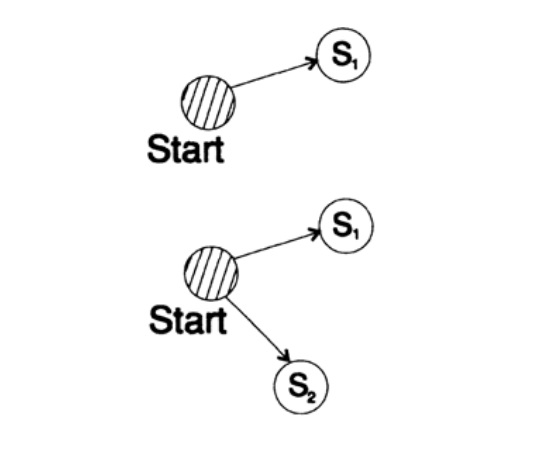图10.V考虑卡夫不等式，它确定了符号代码li的长度的极限值。 在基础2中，不等式表示为
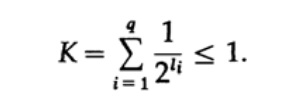
这种不平等现象表明字母不能包含太多的短字符，否则总和将会很大。
为了证明任何快速唯一解码码的卡夫不等式，我们构造了一个解码树并应用了数学归纳法。 如果一棵树有一或两片叶子，如图10.V所示，那么不等式无疑是正确的。 此外，如果树上有多于两片叶子，则将长m的树分成两个子树。 根据归纳原理，我们假定不等式对于高度为m -1或更小的每个分支都是正确的。 根据归纳原理，将不等式应用于每个分支。 表示分支K'和K''的代码长度。 当合并一棵树的两个分支时，每个分支的长度增加1，因此，代码的长度由K'/ 2和K''/ 2之和组成。
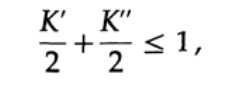
定理被证明。
考虑麦克米伦定理的证明。 我们将卡夫不等式应用于无线程解码代码。 该证明基于以下事实：对于任何K> 1的数，该数的n次幂显然大于n的线性函数，其中n是一个相当大的数。 我们将卡夫不等式提高到n次方，并将表达式表示为和
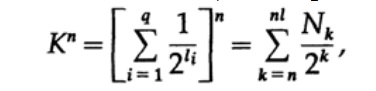
其中Nk是长度为k的字符数，求和以字符的第n个表示形式的最小长度开始，以最大长度nl结束，其中l是编码字符的最大长度。 从唯一解码的要求可以得出以下结论。 金额显示为
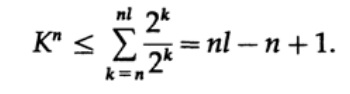
如果K> 1，则必须建立足够大的n，以使不等式变为假。 因此，k <= 1； 麦克米伦定理得到证明。
考虑一些应用卡夫不等式的例子。 是否可以存在长度为1、3、3、3的唯一解码代码？ 是的，因为
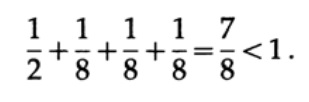
长度1，2，2，3呢？ 根据公式计算
不平等受到侵犯！ 该代码中的短字符太多。
逗号代码是由字符1组成的代码，以字符0结尾，但最后一个字符由全1组成。 特殊情况之一是代码。
s1 = 0; s2 = 10； s3 = 110； s4 = 1110； s5 = 11111。对于此代码，我们获得卡夫不等式的表达式
在这种情况下，我们实现平等。 显而易见，对于点代码，卡夫不等式退化为相等。
编写代码时，需要注意卡夫的数量。 如果卡夫数量开始超过1，则这表示需要包括不同长度的字符以减少平均代码长度。
应该注意的是，卡夫的不等式并不意味着该代码是唯一可解码的，而是存在一个具有这样长度的字符的代码被唯一解码。 要构建唯一的解码代码，您可以在bit li中为相应的长度分配一个二进制数。 例如，对于长度2、2、3、3、4、4、4、4，我们获得卡夫不等式
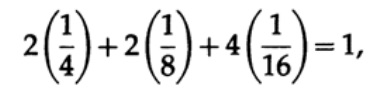
因此，可能存在这种唯一的解码流代码。
s1 = 00； s2 = 01; s3 = 100； s4 = 101；
s5 = 1100； s6 = 1101； s7 = 1110； s8 = 1111；我想关注我们交换想法时实际发生的情况。 例如，在这个时候，我想将想法从我的头转移到你的头上。 我说了一些单词，据我所相信，您可以通过这些单词理解（理解）这个想法。
但是当您稍后想将此想法传达给您的朋友时，几乎可以肯定地说出完全不同的话。 实际上，一个或多个含义没有包含在任何特定的单词中。 我使用了一些单词，您可以使用完全不同的单词来传达相同的想法。 因此，不同的单词可以传达相同的信息。 但是，一旦您告诉对话者您不理解该消息，则对话者通常会选择另一组单词（第二个甚至第三个）来传达含义。 因此，该信息未包含在一组特定的单词中。 收到这些单词后，将这些单词转换为对话者想传达给您的想法时，您会做很多工作。
我们学习选择单词以适应对话者。 从某种意义上说，我们选择与我们的想法和频道中的噪声水平相匹配的词，尽管这样的比较不能准确反映我在解码过程中用来表示噪声的模型。 在大型组织中，一个严重的问题是对话者无法听到别人说的话。 在高级职位上，员工会听到他们“想听到的东西”。 在某些情况下，您在升职时需要记住这一点。 形式化的信息表示是我们生活中过程的部分反映，并且已发现其广泛应用远远超出了计算机应用中形式规则的范围。
待续...谁想帮助翻译，排版和出版本书-用个人电子邮件或电子邮件magisterludi2016@yandex.ru撰写顺便说一下，我们还发布了另一本很酷的书的翻译-
“梦想机器：计算机革命的历史” ）