
这是本文第一部分的继续。
在本文的第一部分中,作者在mail.ru上谈到了针对Agario游戏的竞赛条件,游戏世界的结构以及机器人的结构。 部分是因为它们仅影响神经网络输出处的输入传感器和命令的设备(以下在图片和文字中将使用缩写NN)。 因此,让我们尝试打开黑匣子,了解其中的所有内容。
这是第一张图片:
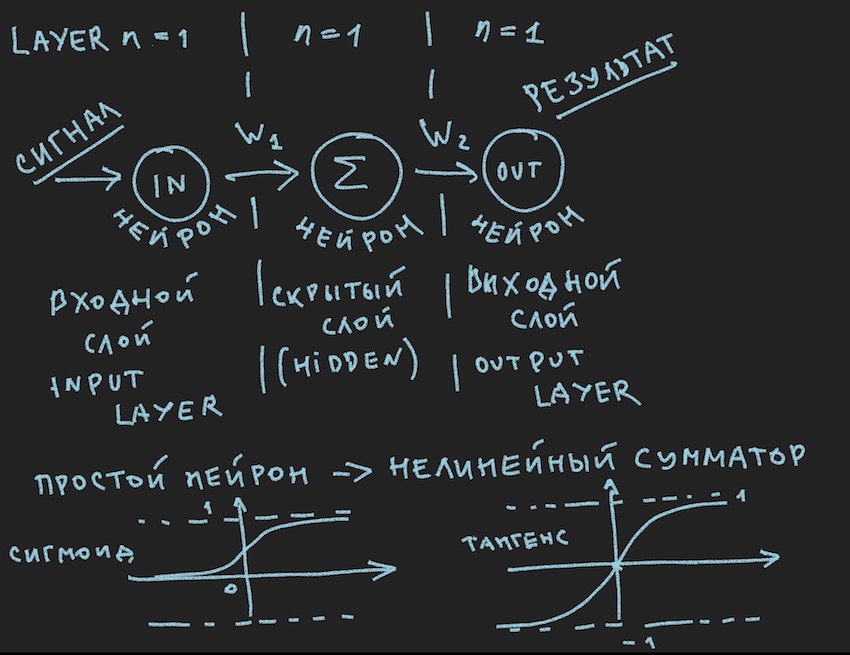
他们示意性地描绘了什么会引起我的读者无聊的笑容,他们又在一年级时再次说过,他们在各种资料来源中都多次出现。 但是,我们实际上确实希望将此图片应用到bot的管理中,因此在重要说明之后,我们将对其进行仔细研究。
重要说明:有大量现成的用于神经网络的解决方案(框架):

所有这些软件包解决了神经网络开发人员的主要任务:NN的构建和训练或“最佳”权重的搜索。 这种搜索的主要方法是反向传播 。 如上链接文章所述,它是上世纪70年代发明的,在此期间,它作为船的底部,已经获得了各种改进,但本质是相同的:以训练示例为基础找到重量系数,每个人都非常希望这些示例中有一个以神经网络的输出信号形式存在的现成答案。 读者可以反对我。 据我所知,已经发明了各种类别和原理的自学网络,但是那里的一切进展都不顺利。 当然,有计划更详细地研究这个动物园,但是我想我会发现志同道合的人发现,即使是最弯曲的DIY制成的自行车,也比理想自行车的传送带复制品更靠近创作者的心脏。
作者意识到游戏服务器很可能不会拥有这些库,并且组织者将其分配为1个处理器核心的计算能力显然不足以使用沉重的框架,因此作者继续创建了自己的自行车。 关于这一点的重要评论结束了。
让我们回到图片,它描述了可能的最简单的具有隐藏层(又名隐藏层或隐藏层)的神经网络。 现在,作者本人一直用这个简单示例的思想稳定地注视着图片,向读者揭示了人工神经网络的深度。 当一切都简化为原始元素时,更容易理解其本质。 底线是隐藏层神经元没有什么可概括的。 而且很可能这甚至不是神经网络,在教科书中,最简单的NN是具有两个输入的网络。 因此,我们就像是最简单的网络中最简单的发现者。
让我们尝试描述这个神经网络(伪代码):
我们以阵列的形式介绍网络拓扑,其中每个元素对应于该层及其中神经元的数量:
int array Topology= { 1, 1, 1}
我们还需要神经网络W的权重的浮点数组,考虑到我们的网络是“前馈神经网络(FF或FFNN)”,其中当前层的每个神经元都连接到下一层的每个神经元,我们得到数组W的维数[层数,层中神经元的数量,层中神经元的数量]。 并不是最理想的编码,但是考虑到GPU在文本中非常接近的地方,这是可以理解的。
我想通过一个简短的CalculateSize过程来计算神经元计数神经元的数量及其在dendritecount神经网络中的连接数,我认为这将更好地向作者解释这些连接的性质:
void CalculateSize(array int Topology, int neuroncount, int dendritecount) { for (int i : Topology) // i neuroncount += i; for (int layer = 0, layer <Topology.Length - 1, layer++) // for (int i = 0, i < Topology[layer] + 1, i++) // for (int j = 0, j < Topology[layer + 1], j++) // dendritecount++; }
我的读者,已经很了解这一切的作者,在第一篇文章中提出了这一观点,当然不会问:为什么在第三嵌套循环拓扑[layer1 + 1]而不是拓扑[layer1]中,它给神经元带来的好处多于网络拓扑中的作用。 我不会回答。 对于读者要求功课也很有用。
我们距离构建有效的神经网络仅一步之遥。 仍然需要增加对神经元输入及其激活的信号求和的功能。 激活函数有很多,但是最接近神经元性质的激活函数是Sigmoid和Tangensoid (最好将其称为,尽管在文献中未使用此名称,但最大值是切线的,但这是图形的名称,尽管如果图形不是函数的反映又是什么图形?)
因此,这里我们具有神经元激活功能(它们存在于图片的下部)
float Sigmoid(float x) { if (x < -10.0f) return 0.0f; else if (x > 10.0f) return 1.0f; return (float)(1.0f / (1.0f + expf(-x))); }
Sigmoid返回值从0到1。
float Tanh(float x) { if (x < -10.0f) return -1.0f; else if (x > 10.0f) return 1.0f; return (float)(tanhf(x)); }
切线返回值从-1到1。
信号通过神经网络的主要思想是波:信号被馈送到输入神经元->通过神经连接,信号进入第二层->第二层的神经元总结通过神经元权重改变了到达它们的信号->通过附加偏置权重添加->我们使用激活函数->和wu-al进入下一层(逐层读取示例中的第一个循环),也就是说,从一开始就重复该链,只有下一层的神经元才会成为输入神经元。 为简化起见,您甚至不需要存储整个网络的神经元值,只需要存储NN权重和活动层神经元的值即可。
再次,我们将信号发送到输入NN,该波穿过各层,在输出层上,我们除去获得的值。
在这里,根据读者的口味,可以使用递归或像作者一样的三重循环以编程方式解决问题,从而加快计算速度,而无需围住神经元及其连接和其他OOP形式的对象。 同样,这是由于GPU运算紧密的感觉,在GPU上,由于其大规模并行性,OOP有点停顿了,这与c#和C ++有关。
此外,还邀请读者自愿地独立地使用代码来构建神经网络,对于作者来说,缺少它是非常清楚和熟悉的, 例如,从头开始构建NN的示例中,网络中有很多示例,因此很难误入歧途,就像那样就像上图中的直接分布神经网络一样简单。
但是,尚未离开上一段落的读者会惊叹于何处,并且是正确的。在童年时期,作者通过插图确定了这本书的价值。 您在这里:
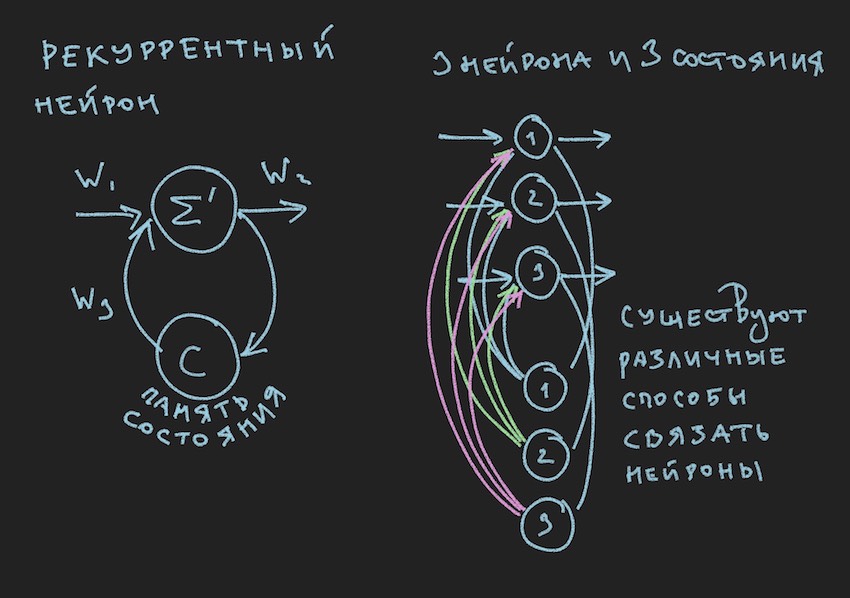
在图片中,我们看到了递归神经元,由这种神经元构建的NN被称为递归神经元或RNN。 指定的神经网络具有短期记忆,并被作者选择为机器人,以适应游戏过程。 当然,作者建立了直接分布神经网络,但是在寻找“有效”解决方案的过程中,他切换到了RNN。
循环神经元具有附加状态C,该状态在信号第一次通过时间轴上的神经元Tick + 0传递之后形成。 简单来说,这是神经元输出信号的副本。 在第二步中,读取Tick +1(因为网络以游戏机器人和服务器的频率运行),值C通过附加权重返回到神经层的输入,因此参与了信号的形成,但已经达到Tick +1倍了。
注意: 在有关NN游戏机器人管理的研究小组的工作中 ,倾向于将两个节奏用于神经网络,一个节奏是游戏Tick的频率,例如第二个节奏的速度是第一个节奏的两倍。 NN的不同部分以不同的频率运行,从而使人对NN内部的游戏情况有不同的认识,从而提高了灵活性。
为了在bot代码中构建RNN,我们在拓扑中引入了一个额外的数组,其中每个元素对应于该层以及其中的神经状态数:
int array TopologyNN= { numberofSensors, 16, 8, 4}
int array TopologyRNN= { 0, 16, 0, 0 }
从上面的拓扑可以看出,第二层是循环的,因为它包含神经状态。 我们还以WRR数组的浮点形式(与W数组尺寸相同)引入其他权重。
我们的神经网络中的连接数将有所变化:
for (int layer = 0, layer < TopologyNN.Length - 1, layer++) for (int i = 0, i < TopologyNN[layer] + 1, i++) for (int j = 0, j < TopologyNN[layer + 1] , j++) dendritecount++; for (int layer = 0, layer < TopologyRNN.Length - 1, layer++) for (int i = 0, i< TopologyRNN[layer] + 1 , i++) for (int j = 0, j< TopologyRNN[layer], j++) dendritecount++;
作者将在本文的结尾处附加一个递归神经网络的通用代码,但要理解的主要原理是:在递归NN的情况下,波穿过层的传递不会从根本上改变任何东西,仅向神经元激活函数添加一个术语。 这是前一个Tick上的神经元状态乘以神经连接权重的术语。
我们假设神经网络的理论和实践已经更新,但是作者清楚地意识到,他并没有使读者更进一步地了解如何教授这种简单的神经网络结构以在游戏中做出任何决定。 我们没有包含用于教授NN的示例的库。 在由机器人开发人员组成的Internet小组中,有一种意见:以机器人坐标和其他游戏信息的形式给我们提供一个日志文件,以构成示例库。 但是,不幸的是,作者无法弄清楚如何使用此日志文件来训练NN。 我将很高兴在文章的评论中对此进行讨论。 因此,作者可以用来理解训练方法或找到“有效”神经平衡(神经连接)的唯一方法是遗传算法。
准备了有关遗传算法原理的图片:
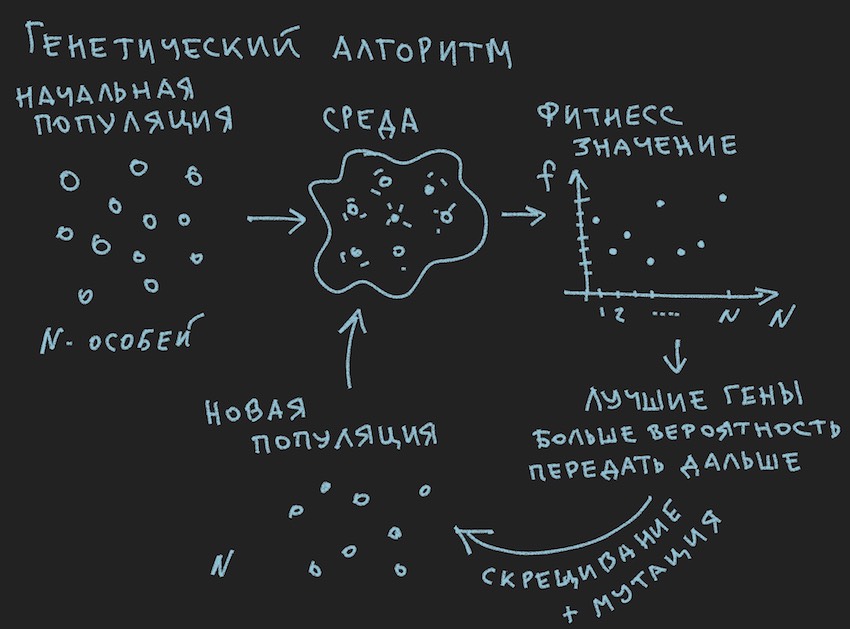
于是遗传算法 。
作者将尝试不深入研究此过程的理论 ,而只回忆起继续完整阅读本文所必需的最低要求。
在遗传算法中,主要工作流体是基因(DNA是分子的名称)。 在我们的案例中,基因组是一组连续的基因或一维浮点长序列。
在使用新建的神经网络的初始阶段,有必要对其进行初始化。 初始化是指将-1到1的随机值分配给神经平衡,作者遇到提到-1到1的值范围太极端 ,训练网络的权重范围较小,例如,从-0.5到0.5,应该将初始值范围设置为优秀从-1到1。但是我们将采用经典的方法来收集所有困难,并以尽可能大的初始随机变量段作为初始化神经网络的基础。
现在将出现双射 。 我们将假设bot基因组的长度(大小)等于神经网络TopologyNN.Length + TopologyRNN.Length的总长度,这并非是作者花了很多时间在计算神经连接的过程上。
注意:正如读者已经为他自己指出的那样,我们仅将神经网络的权重传递给基因型,连接结构,激活功能和神经元状态不会被传递。 对于遗传算法,仅神经连接就足够了,这表明它们是信息的载体。 在某些情况下,遗传算法还会改变神经网络中连接的结构,并且实现起来非常简单。 在这里,作者为读者留下了创造力的空间,尽管他本人会很感兴趣地思考它:您需要了解使用两个独立的基因组和两个适应度函数(简化的两个独立的遗传算法),或者都可以使用相同的基因和算法。
并且由于我们使用随机变量初始化了NN,因此我们也初始化了基因组。 逆过程也是可能的:通过随机变量初始化基因型,然后将其复制到神经权重中。 第二种选择很常见。 由于程序中的遗传算法通常存在于本质本身之外,并且仅与基因组数据和适应度函数的值相关联...停止,停止,读者会说,图片清楚地显示了种群而不是单个基因组的单词。
好的,将一些图片添加到读者的头脑炉中:
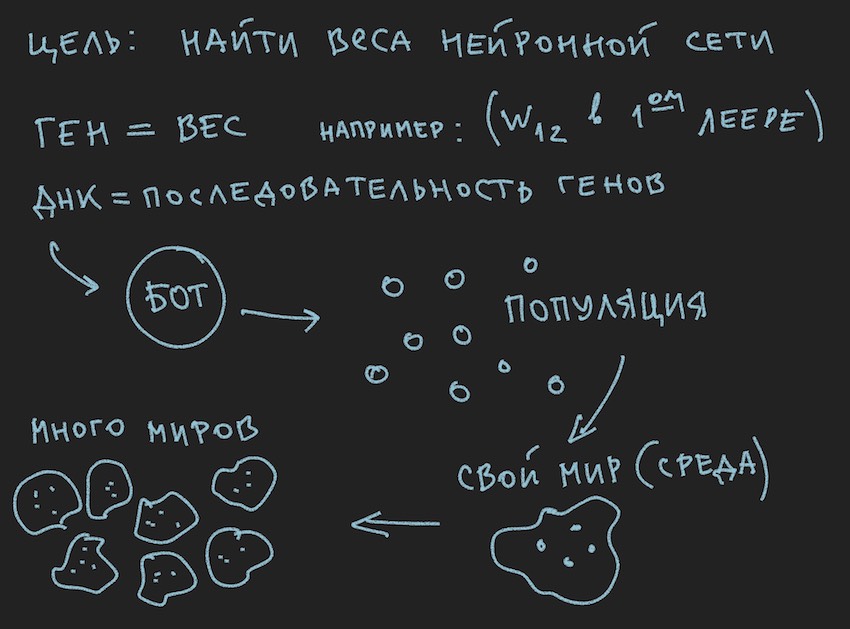
由于作者在写文章文字之前画了这些图片,因此它们支持文字,但不跟着当前故事的字母开头。
从所获信息中可以得出,遗传算法的主要工作主体是基因组 。 这与作者先前所说的有些相反,但是在现实世界中如何做到没有小矛盾。 昨天,太阳绕着地球旋转,今天,作者讨论了该软件bot内部的神经网络。 难怪他还记得理性的烤箱。
我相信读者本人可以解决世界矛盾的问题。 机器人世界完全是本文的自给自足。
但是对于本文的这一部分,作者已经设法做到的是形成大量的机器人。
让我们从软件方面看一下:
有一个Bot(它可以是OOP中的一个对象,也可以是一个结构,尽管它也可能是对象或只是数据数组)。 在内部,Bot包含有关其坐标,速度,质量的信息以及在游戏过程中有用的其他信息,但是对我们而言,现在最主要的是,它包含指向其基因型或基因型本身的链接,具体取决于实现方式。 然后,您可以采取不同的方式,将自己限制在神经网络权重数组中,或者引入其他基因型数组,因为这将方便读者在他们的想象中进行想象。 在第一阶段,作者在程序中分配了神经平衡和基因型阵列。 然后,他拒绝重复信息,并将自己局限于神经网络的权重。
按照故事的逻辑,您需要告诉机器人的数量是上述机器人的一个数组。 什么游戏循环...再次停止,什么游戏循环? 开发人员有礼貌地为服务器上的游戏世界模拟程序中的一个Bot或一个本地模拟器中的最多四个bot提供了一个位置。 如果您还记得作者选择的神经网络的拓扑:
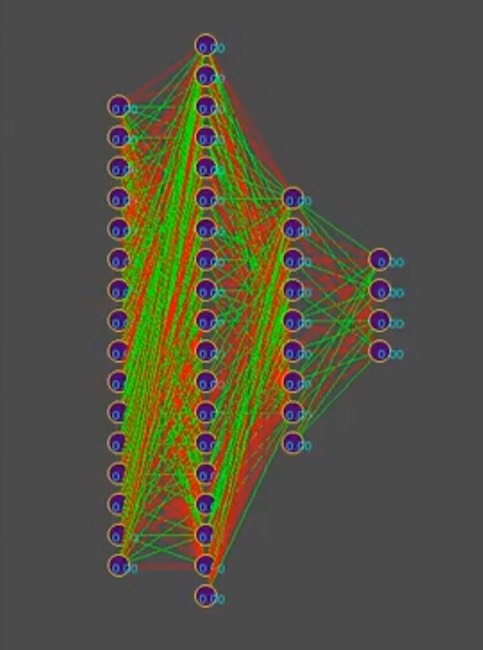
为了简化故事,假设该基因型包含大约1000个神经连接,顺便说一下,在模拟器中,基因型如下所示(红色是负基因值,绿色是正值,每行是一个单独的基因组):

照片上的注释:随着时间的流逝,模式在解决方案之一的主导方向上发生变化,垂直条纹是常见的基因型基因。
因此,我们从比赛的组织者那里获得了1000个基因型基因,并且在游戏世界模拟器程序中最多有四个机器人。 您需要模拟几次机器人大战,以便即使是最聪明的人也可以通过蛮力接近“有效”
基因型,请阅读神经连接的“有效”组合,条件是每个神经连接的步长在-1到1之间变化,哪一步呢? 初始化是随机浮动,它是15个小数位。 我们尚不清楚这一步骤。 关于神经权重组合的变体数,作者假设这是一个无限数,当选择某个步长时,可能是一个有限数,但是无论如何,即使考虑从机器人队列中依次启动加上官方模拟器的同时并行启动,这些数字在模拟器中的位置也要多于4个。在一台计算机上(对于老式编程的爱好者:计算机)。
希望这些图片对读者有所帮助。
在这里您需要暂停讨论软件解决方案的体系结构。 由于以单独的软件bot形式上传到比赛站点的解决方案不再适用。 必须在组织者生态系统和试图为他找到神经网络配置的程序的框架内,根据比赛规则将机器人程序分开。 下图取自会议的演示文稿,但通常反映了真实情况。
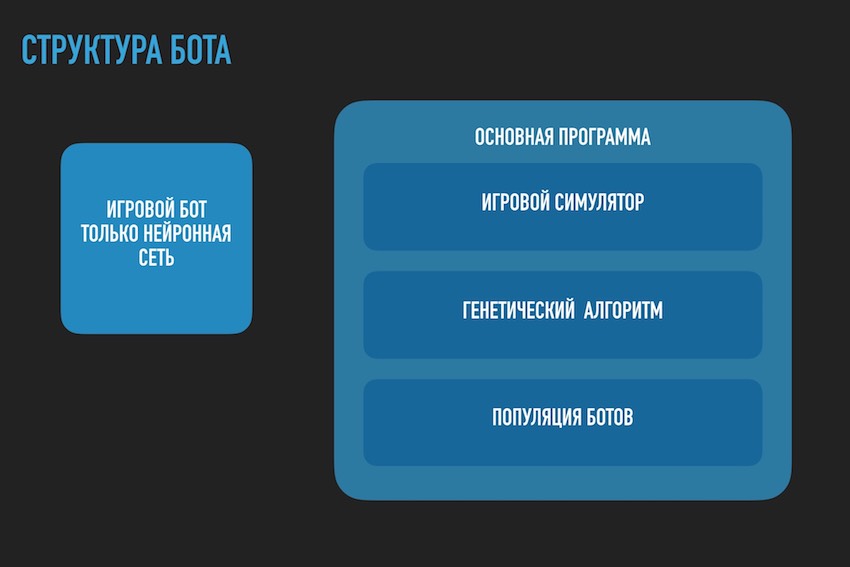
他回想起一个胡闹的笑话:
大型组织。
时间18.00,所有员工合为一体。 突然,一名员工关闭计算机,穿好衣服离开。
每个人都惊讶地看着他。
第二天 同一员工在18.00关闭计算机并离开。 每个人都继续工作,并开始不高兴地窃窃私语。
第二天。 同一位员工在18.00关闭计算机...
一位同事接近他:
-由于您不感到羞耻,我们正在工作,本季度末,有许多报告,我们也希望准时回家,您真是个好人...
-伙计们,我通常在度假!
...待续。
是的,我几乎忘记附加RNN计算过程代码,它是有效的并且独立编写,因此可能其中有错误。 为了进行放大,我将按原样使用它,它是用c ++应用于CUDA(用于在GPU上进行计算的库)的。
注意:多维数组在GPU上不能很好地相处,当然会有纹理和矩阵计算,但是它们建议使用一维数组。
例如,尺寸为M乘以j的数组[i,j]会变成[i * M + j]形式的数组。
RNN计算程序的源代码 __global__ void cudaRNN(Bot *bot, argumentsRNN *RNN, ConstantStruct *Const, int *Topology, int *TopologyRNN, int numElements, int gameTick) { int tid = blockIdx.x * blockDim.x + threadIdx.x; int threadN = gridDim.x * blockDim.x; int TopologySize = Const->TopologySize; for (int pos = tid; pos < numElements; pos += threadN) { const int ii = pos; const int iiA = pos*Const->ArrayDim; int ArrayDim = Const->ArrayDim; const int iiAT = ii*TopologySize*ArrayDim; if (bot[pos].TTF != 0 && bot[pos].Mass>0) { RNN->outputs[iiA + Topology[0]] = 1.f; //bias int neuroncount7 = Topology[0]; neuroncount7++; for (int layer1 = 0; layer1 < TopologySize - 1; layer1++) { for (int j4 = 0; j4 < Topology[layer1 + 1]; j4++) { for (int i5 = 0; i5 < Topology[layer1] + 1; i5++) { RNN->sums[iiA + j4] = RNN->sums[iiA + j4] + RNN->outputs[iiA + i5] * RNN->NNweights[((ii*TopologySize + layer1)*ArrayDim + i5)*ArrayDim + j4]; } } if (TopologyRNN[layer1] > 0) { for (int j14 = 0; j14 < Topology[layer1]; j14++) { for (int i15 = 0; i15 < Topology[layer1]; i15++) { RNN->sumsContext[iiA + j14] = RNN->sumsContext[iiA + j14] + RNN->neuronContext[iiAT + ArrayDim * layer1 + i15] * RNN->MNweights[((ii*TopologySize + layer1)*ArrayDim + i15)*ArrayDim + j14]; } RNN->sumsContext[iiA + j14] = RNN->sumsContext[iiA + j14] + 1.0f* RNN->MNweights[((ii*TopologySize + layer1)*ArrayDim + Topology[layer1])*ArrayDim + j14]; //bias=1 } for (int t = 0; t < Topology[layer1 + 1]; t++) { RNN->outputs[iiA + t] = Tanh(RNN->sums[iiA + t] + RNN->sumsContext[iiA + t]); RNN->neuronContext[iiAT + ArrayDim * layer1 + t] = RNN->outputs[iiA + t]; } //SoftMax /* double sum = 0.0; for (int k = 0; k <ArrayDim; ++k) sum += exp(RNN->outputs[iiA + k]); for (int k = 0; k < ArrayDim; ++k) RNN->outputs[iiA + k] = exp(RNN->outputs[iiA + k]) / sum; */ } else { for (int i1 = 0; i1 < Topology[layer1 + 1]; i1++) { RNN->outputs[iiA + i1] = Sigmoid(RNN->sums[iiA + i1]); //sigma } } if (layer1 + 1 != TopologySize - 1) { RNN->outputs[iiA + Topology[layer1 + 1]] = 1.f; } for (int i2 = 0; i2 < ArrayDim; i2++) { RNN->sums[iiA + i2] = 0.f; RNN->sumsContext[iiA + i2] = 0.f; } } } } }