
质数的属性很少允许您以不同于预计算数组形式的方式使用它们-并且最好是尽可能地庞大。 具有一位或另一位数字的整数形式的自然存储格式同时遭受一些缺点,这些缺点随着数据量的增长而变得越来越明显。
因此,具有这样一个表的大小的16位无符号整数的格式约为13 KB,它仅包含6542个质数:其后是数字65531,是较高位深度的值。 这样的桌子仅适合作为玩具。
编程中最流行的32位整数格式看起来更加扎实-它使您可以存储约2.03亿个简单的整数。 但是这样的表已经占用了约775兆字节。
64位格式具有更大的前景。 但是,如果理论上的幂为1e + 19值,则该表的大小为64艾字节。
并非真正相信我们的进步人类将在可预见的将来计算出如此数量的素数表。 而且这里的重点不在于数量,甚至在于可用算法的计数时间。 假设,如果仍然可以在几个小时内独立地计算所有32位简单表的表(图1),那么对于表至少大一个数量级的情况,将需要几天的时间。 但是今天的交易量-这仅仅是初始水平。
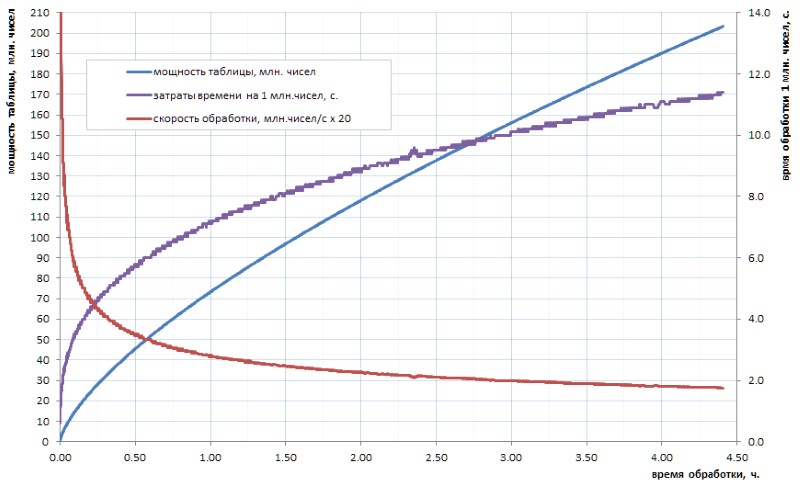
从该图可以看出,启动急动之后的特定计算时间平稳地过渡到渐近增长。 他很慢。 但这就是增长,这意味着随着时间的推移挖掘每个下一个数据将变得越来越困难。 如果要取得重大突破,则必须跨内核并行化工作(并且并行性很好),并将其挂在超级计算机上。 有望在一周内实现前100亿个简单项目,而仅在一年内就获得1000亿个简单项目。 当然,比我的家庭作业中使用的琐碎胸像有更快的算法来计算简单,但是从本质上讲,这不会改变问题:经过两个或三个数量级后,情况变得相似。
因此,一旦执行了计数工作,将其结果存储为现成的表格形式,并根据需要使用它,将是很好的。
由于这个想法的显而易见性,网络上有许多链接,这些链接指向某人已经计算出的素数的现成清单。 las,在大多数情况下,它们仅适合于学生手工艺品:例如,一种在各地徘徊,其中包括5000万个简单的工艺品。 这个数目只能使初学者惊讶不已:上面已经提到过,在家用计算机上,您可以在几个小时内独立计算所有32位简单表的表,它的大小是原来的四倍。 大概在15到20年前,这样的清单确实是非专业人士的一项英雄成就。 如今,在多核数千兆赫兹和数千兆字节设备的时代,这已不再令人印象深刻。
我很幸运能够接触到更具代表性的简单表格,我将进一步使用该表格作为说明,并为我的现场实验做出牺牲。 出于阴谋目的,我将其称为1TPrimo 。 它包含所有小于一万亿的素数。
以1TPrimo为例,您可以轻松查看要处理的卷。 该列表的容量约为376 GB(64位整数格式),容量为280 GB。 顺便说一下-可以容纳32位数字的那部分仅占其中所表示数字的0.5%。 这绝对清楚地表明,任何使用素数的严肃工作都不可避免地趋向于总64位(或更多)位深度。
因此,令人沮丧的趋势是显而易见的:以某种方式严重的素数表不可避免地具有钛酸体积。 我们必须以某种方式与之抗争。
查看表(图2)时首先想到的是,它由几乎相同的连续值组成,这些值仅在最后一个小数点后一位或两个小数位不同:
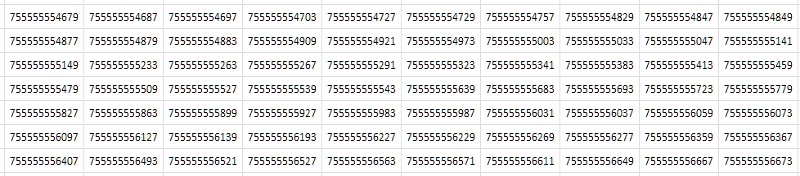
简单来说,从最一般的抽象角度考虑:如果文件中包含大量重复数据,则存档程序应将其很好地压缩。 实际上,在标准设置下使用流行的7-zip实用程序对1TPrimo表进行压缩的压缩率非常高:8.5。 的确,在8核服务器上,由于源表的容量很大,处理时间为14小时12分钟,而该服务器的所有核的平均负载约为80-90%。 通用压缩算法是为一些抽象的,关于数据的广义概念而设计的。 在某些特殊情况下,基于传入数据集众所周知的功能构建的专用压缩算法可以展示出更为有效的指标,这项工作专门针对这些指标。 以及如何有效将在下面变得清晰。
相邻素数的接近数值要求做出决定,而不是自己存储这些值,而是决定它们之间的间隔(差值)。 在这种情况下,由于间隔的位深度远低于初始数据的位深度(图3),因此可以实现显着的节省。
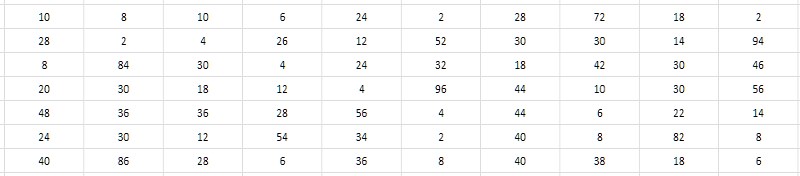
似乎它不依赖于生成间隔的简单位的位深度。 详尽的搜索显示,从1TPrimo表中各个位置获取的质数的间隔的典型值位于单位,数十个,有时甚至数百个单位之内,并且-作为第一个工作句-它们可能适合8位范围无符号整数,即字节。 这将非常方便,并且与64位格式相比,这将立即导致8倍数据压缩-刚好在7-zip归档程序所演示的水平。 此外,与7-zip相比,压缩和解压缩算法的简单性原则上应对压缩和访问数据的速度都产生重大影响。 听起来很诱人。
绝对清楚,从其绝对值转换为它们之间的相对间隔的数据仅适用于恢复从主表的最开始连续一行的一系列值。 但是,如果我们在这样的间隔表中添加最小的块索引结构,那么额外的开销开销将很小,这将使我们能够(但已逐块)还原表元素(通过其编号)和最接近的元素(通过任意设置的值)以及这些操作以及主操作序列样本-通常,它会耗尽对此类数据的大部分可能查询。 当然,统计处理将变得更加复杂,但仍将保持相当透明,因为 访问所需的数据块时,从可用间隔“即时”恢复它没有特别的技巧。
但是a。 一个关于1TPrimo数据的简单数值实验表明,已经到了第三千万个末尾(这还不到1TPrimo量的百分之一),然后到其他地方,相邻素数之间的间隔通常都在0..255范围之外。
尽管如此,一个稍微复杂的数值实验表明,相邻素数之间最大间隔的增长与表格本身的增长非常非常慢-这意味着该想法在某种程度上还是不错的。
第二,仔细查看间隔表,可以发现不是存储差异本身,而是存储一半。 由于所有大于2的素数显然分别是奇数,因此它们的差显然是偶数。 因此,差异可以减少2而不会损失价值; 为了完整起见,也可以从获得的商中减去1,以有用地使用否则未要求的零值(图4)。 与松散的,多孔的初始形式相反,这种间隔的减小将在下文中称为整体式,在这种形式中,所有奇数和零都被认为是无用的。
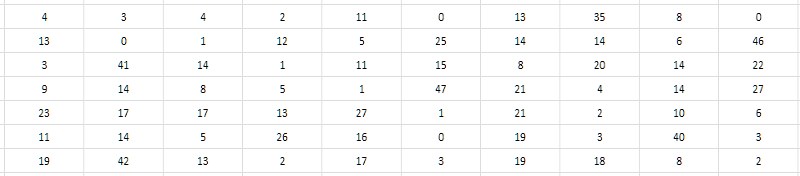
应当注意,由于前两个简单的间隔(2和3)之间的间隔不适合此方案,因此必须从间隔表中排除2,并始终牢记这一事实。
这种简单的技术使您可以将2到512的间隔编码在0..255的值范围内,再次使人们感到希望,差分方法将使我们能够打包更强大的素数序列。 的确如此:在1TPrimo列表中显示的376亿个值表明,只有6个(六个!)间隔不在2..512范围内。
但这是个好消息。 不好的是,这六个间隔很随意地散布在列表中,并且第一个间隔已经出现在列表的前三分之一的末尾,这使得其余三分之二变成不适合这种压缩方法的镇流器(图5):
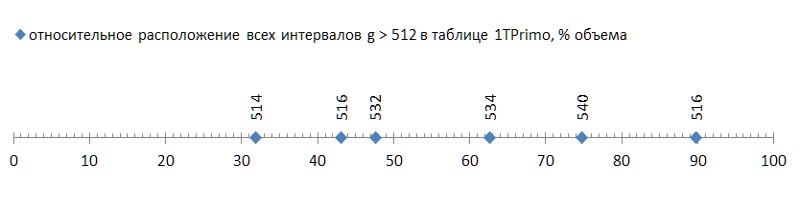
这样的冲洗(有些不幸的六块,价值将近四百亿!-还有你……)甚至用药膏来进行比较,以显示焦油的荣誉。 但是,这是一种模式,不是偶然的。 如果我们根据数据的长度来追踪素数之间的间隔的首次出现,那么很明显,这种现象存在于素数的遗传中,尽管它的发展非常缓慢(图6 *)。
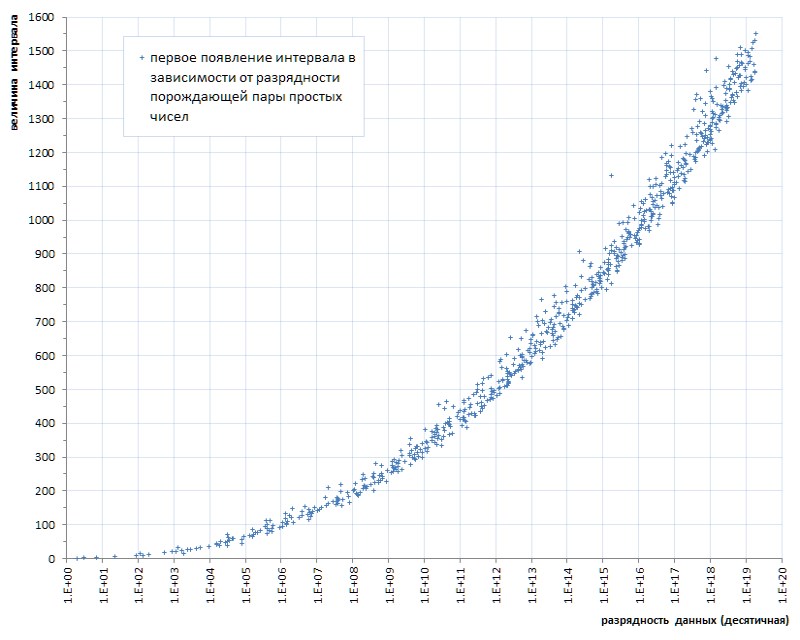
*根据Thomas R. Nisley的主题网站编制的时间表 ,
这比1TPrimo列表的功能高出几个数量级
但是,即使这一非常缓慢的进展也明确地暗示:只有在列表的某个预定功率下,才能将自己限制为某个间隔的某个预定位深度。 也就是说,它不适合作为通用解决方案。
但是,所提出的压缩素数序列的方法使您可以实现一个容量接近120亿个值的简单紧凑表的事实已经是相当不错的结果。 这样的表占用的空间为11.1 GB,而普通的64位格式为89.4 GB。 当然,对于许多应用来说,这种解决方案可能就足够了。
有趣的是:仅使用一个处理器内核就将具有块结构的64位1TPrimo表转换为具有块结构的8位间隔格式的过程(对于并行化,您必须诉诸程序的极大复杂性,这绝对不值得)并且不超过5个处理器负载的百分比(大部分时间都花在文件操作上)仅花费了19分钟。我记得-在8个内核上14小时的时间是7-zip归档程序所花费负载的80-90%。
当然,仅对表的前三分之一进行了转换,间隔的范围不超过512。因此,如果将整整14小时带到同一三分之一,则应该将19分钟与7-zip存档器的近5小时进行比较。 在可比较的压缩量(8和8.5)下,差异约为15倍。 考虑到广播节目的大部分工作时间都由文件操作占据,因此在更快的磁盘系统上,差异甚至会更大。 从理智上讲,仍然应该在一个线程上计算在8个内核上使用7-zip的运行时间,然后进行比较就可以了。
从这样的数据库中进行选择的时间与从解压缩数据表中进行选择的时间相差很小,并且几乎完全由文件操作时间决定。 具体数量强烈取决于具体的硬件,在我的服务器上,平均而言,访问任意数据块的时间为37.8μs,而顺序读取块-每个块4.2μs,以完全解压缩该块-小于1μs。 也就是说,将数据的解压缩与标准存档器的工作进行比较是没有意义的。 这是一大优势。
最后,观察结果提供了另一种第三种解决方案,该解决方案消除了对数据功效的任何限制:使用可变长度值编码间隔。 长期以来,该技术已广泛用于与压缩相关的应用中。 其含义是,如果在输入中发现经常找到一些值,一些不那么常见,而有些则很少,那么我们可以用短代码编码第一个,使用更可靠的代码编码第二个,第三个-非常长(甚至可能很长,因为没关系:同样,此类数据非常少见)。 结果,接收到的代码的总长度可以比输入数据短得多。
在查看图7中间隔出现的图形时,我们可以假设间隔为2、4、6等。 出现时间间隔早于间隔(例如100、102、104等),那么前者应比后者继续出现更多的频率。 反之亦然-如果间隔514仅从119.9亿开始,间隔516-从162亿开始,而518-通常仅从877亿开始,那么它们将很少遇到。 也就是说,先验地,我们可以假设素数序列中区间的大小与其频率之间存在反比关系。 这意味着-您可以构造一个简单的结构,为它们实现可变长度代码。
当然,关于间隔频率的统计应该成为确定特定编码方法的选择。 幸运的是,与任意数据相反,素数之间的间隔频率-本身是严格确定的,一劳永逸的给定序列-也是严格确定的,一劳永逸的。
图7显示了整个1TPrimo列表的间隔的频率响应:
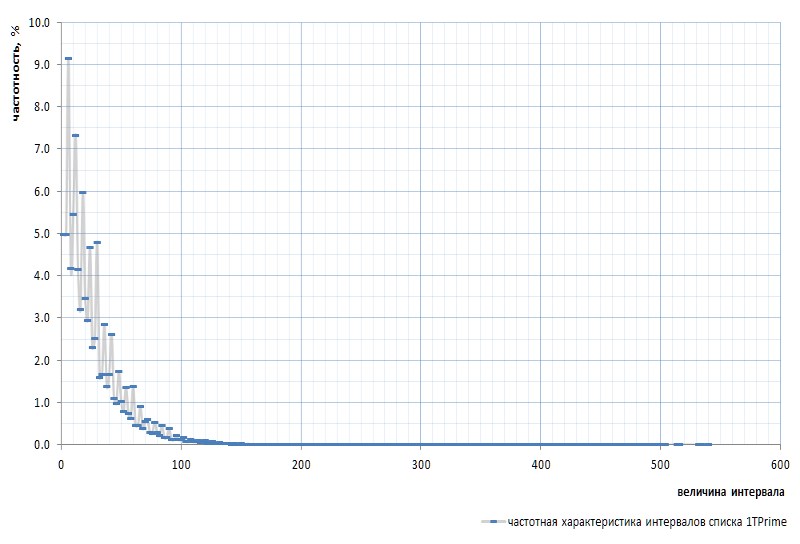
在这里有必要再次提及,图中最前面的质数2和3之间的间隔被排除在外:该间隔为1,并且在质数序列中仅发生一次,而与列表的功效无关。 这个间隔是如此特殊,以至于从简单的列表中删除2而不是不断地误入保留位置。 sim声明数字2是虚拟素数 :在列表中不可见,但在那里。 像那个地鼠。
乍一看,频率图完全确认了以上几段给出的先验假设。 它清楚地显示了间隔的统计异质性以及小数值与大数值相比的高频率。 但是,在第二个更凸的视图中,该图变得更加有趣(图8):
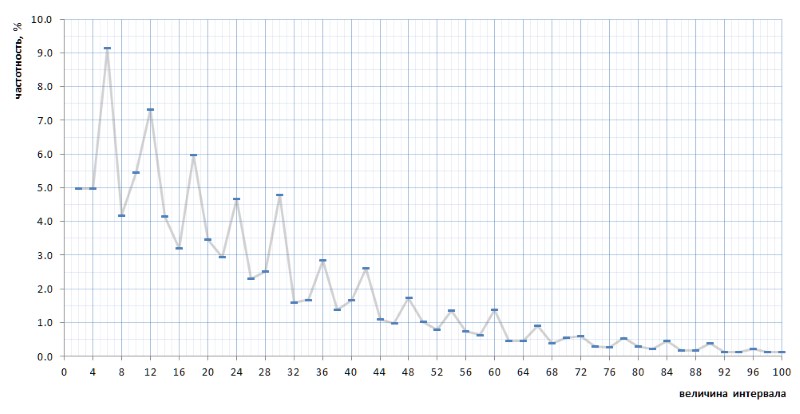
出乎意料的是,事实证明,最频繁的间隔不是2和4,这似乎是出于一般考虑,而是6、12和18,然后是10-然后只有2和4的频率几乎相等(相差7位数字)小数点后)。 而且,在整个图形中都跟踪了数字6的峰值的多重性。
更有趣的是,该图的这种无意揭示的性质是通用的-并且,在所有细节上,它的所有类似之处-在1TPrimo列表表示的整个简单区间序列中,它很可能在任何简单区间序列中都是通用的(当然,如此大胆的声明需要证明,我很高兴将其转移到数论专家的肩膀上。 图10显示了在1TPrimo列表中的任意位置(其他颜色的线)与有限时间间隔采样所得到的全时间间隔统计信息(红线)的比较:
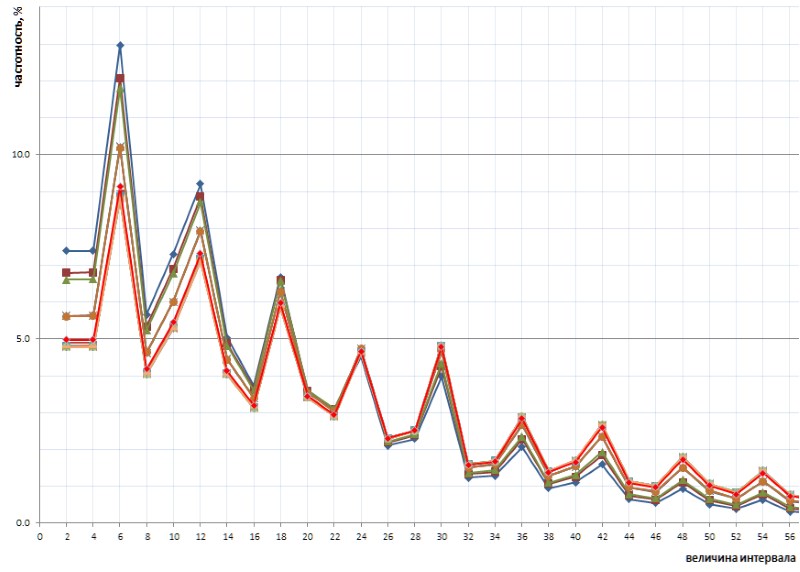
从该图可以看出,所有这些样本彼此完全重复,而图的左右部分仅稍有不同:它们似乎围绕间隔点沿逆时针方向略微旋转,值为24。这种旋转可能是由于以下事实:图形的某些部分建立在具有较低位深度的样本上。 在这样的样本中,根本没有,或者很少有大的间隔,这在具有更高比特深度的样本中变得频繁。 因此,它们的缺失有利于具有较低值的间隔的频率。 在具有较高位深度的样本中,会出现许多具有较大值的新间隔;因此,较小间隔的频率会稍微降低。 随着列表功能的增强,枢轴点很可能会向更大的值转移。 在该图旁边的某个位置是图形的平衡点,其中右侧所有值的总和大约等于左侧所有值的总和。
间隔频率的这种有趣的性质表明放弃了可变长度代码的琐碎结构。 通常,这种结构由各种长度和目的的比特包组成。 例如,首先是将一定数量的前缀位设置为特定值,例如0。在它们后面有一个停止位,该停止位应指示前缀的完成,因此,与前缀应不同:在这种情况下为1。 该前缀可能没有任何长度,也就是说,一遍又一遍,采样可以立即从停止位开始,从而确定最短的序列。 停止位通常后跟一个后缀,后缀的长度由前缀的长度以某种预定的方式确定。 , , — . , - . - (, , - ) , .
, .
在这里,还需要说明一件事。 乍一看,观察到的循环性意味着将间隔分为三元组: {2,4, 6 } , {8,10, 12 } , {14,16, 18 }等(每个三元组中出现频率最高的值都以粗体标出) 。 但是,实际上,这里的周期略有不同。
我不会引用整个推理过程,事实上,这并不存在:这是一种直观的猜测,并辅以一种对选项,计算和样本进行钝性枚举的方法,该方法间歇地花费了几天。 结果显示的周期性包括六个间隔{2,4, 6 ,8,10, 12 } , {14,16, 18 ,20,22, 24 } , {26,28, 30 ,32,34, 36 }和等等(最大频率的间隔再次以粗体突出显示)。
简而言之,提出的打包算法如下。
将间隔分成偶数个六分之一可以使我们以g = i * 12 + t的形式表示任何间隔g ,其中i是该间隔所属的六个数的索引( i = {0,1,2,3, ...} ),并且t是表示集合{2,4,6,8,10,12}任何六个的刚性定义,有界且相同的值之一的尾部。 上面突出显示的索引的频率响应几乎与它的值成反比,因此将六个索引转换为可变长度代码的琐碎结构是合乎逻辑的,上面给出了一个示例。 钳子的频率特性使您可以将其分为两组,这些组可以用不同长度的位链进行编码:最常发现的值6和12用一位进行编码,很少见到的值2、4、8和10用两位进行编码。 当然,需要更多一点来区分这两个选项。
包含位数据包的数组由固定字段补充,这些字段指定了块中显示的数据的起始值,以及从块中存储的间隔恢复任意简单或简单序列所需要的其他数量。
除了这种块索引结构之外,与固定位间隔相比,可变长度代码的使用还由于额外的成本而变得复杂。
当使用固定大小的间隔时,通过序列号确定要搜索质数的块是一个相当简单的任务,因为每个块的间隔数是预先已知的。 但是寻找最接近的值的简单解决方案并没有直接的解决方案。 另外,您可以使用一些经验公式,让您以所需的间隔找到近似的程序段号,然后必须通过详尽搜索来搜索所需的程序段。
对于具有可变长度代码的表,两个任务都需要相同的方法:按数字获取值和按值搜索。 由于代码的长度是变化的,所以事先不知道在任何特定的块中存储了多少差异,以及期望值位于哪个块中。 实验确定,如果块大小为512字节(包括一些标头字节),则块容量可以达到平均值的10-12%。 较小的块会产生更大的相对散射。 同时,随着表的增加,块容量的平均值本身趋于缓慢降低。 为了不精确地确定初始块以按数量和按值搜索期望值,选择经验公式是不平凡的任务。 另外,您可以使用更复杂,更复杂的索引。
实际上,仅此而已。
下面,将以更正式和更详细的方式描述使用可变长度代码压缩素数表的精妙之处以及与其相关的结构,并给出用于C中打包和解包间隔功能的代码。
结果。
从表1TPrimo转换为可变长度代码的数据量为26,309,295,104字节(24.5 GB),并辅以块索引结构(也将在下面介绍),压缩率达到11.4。 显然,随着位深度的增加,压缩率将增加。
新格式的1TPrimo表的280 GB广播时间为1小时。 这是将间隔打包为单字节整数后的预期结果。 在这两种情况下,源表的转换主要由文件操作组成,并且几乎不加载处理器(在第二种情况下,由于算法的计算复杂性较高,因此加载仍然较高)。 数据访问时间与单字节间隔也没有太大区别,但是由于提取可变长度代码的算法复杂性较高,因此解压缩相同大小的完整块所需的时间为1.5μs。
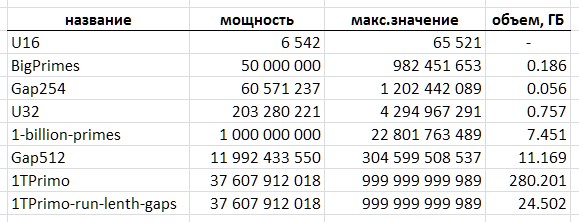
该表(图10)总结了本文中提到的质数表的体积特征。
压缩算法说明
条款和符号
P (prime): P1=3, P2=5, P3=7 ... Pn, Pn1根据其序列号为素数。 我再次(也是最后一次)强调
P0=2是一个虚拟素数。 为了形式上的统一,此数字实际上不包括在素数列表中。
G (gap) -两个连续素数之间的间隔Gn = Pn1 - Pn; G={2,4,6,8 ...} Gn = Pn1 - Pn; G={2,4,6,8 ...}
D (dense) -减小为单片形式的间隔: D = G/2 -1; D={0,1,2,3 ...} D = G/2 -1; D={0,1,2,3 ...} 整体形式的六个间隔看起来像{0,1,2,3,4,5}, {6,7,8,9,10,11}, {12,13,14,15,16,17}等
Q (quotient) -将六的索引简化为整体形式, Q = D div 6; Q={0,1,2,3 ...} Q = D div 6; Q={0,1,2,3 ...}
R (remainder) -六个R = D mod 6. R的余数R = D mod 6. R的值始终在{0,1,2,3,4,5}范围内。
通过上述方法从任意间隔G获得的Q和R值,由于其稳定的频率特性,将以可变长度比特包的形式进行压缩和存储,如下所述。 数据包中编码Q和R值的位串以不同的方式创建:为了编码Q索引,使用前缀H ,通量F和辅助位S的位链,并S缀X和辅助位A的位组对其余R进行编码R
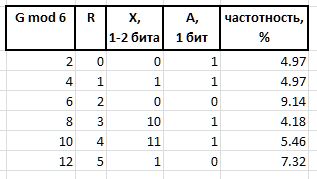
A (arbiter) -确定中缀X大小的位:0-一位中缀,1-两位。
X (infix) -1或2位中缀,与仲裁器位R表格的形式相互确定R的值(该表还显示了前6个带有此类中缀的频率,以供参考):
F (fluxion)是一种通量,是变长L={0,1,2...}的索引Q派生词,旨在区分位字符串(), 0, 00, 000,或1, 01, 001等的语义。 d。
长度为L的单位的位链表示为2^L - 1 (符号^表示幂)。 在C表示法中,可以通过表达式1<<L - 1获得相同的值。 然后可以Q表达式从Q获得长度为L的通量值
F = Q-(1 << L-1),
并通过表达从通量恢复Q
Q =(1 << L-1)+ F.
例如,对于数量Q = {0..15} ,将获得以下磁通量比特链:
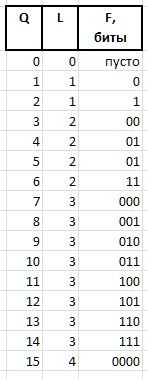
打包/恢复值所需的最后两位字段是:
H (header) -前缀,设置为0的位字符串。
S (stop) -停止位设置为1,结束前缀。
实际上,这些位是首先在位串中处理的,它们使您可以确定在拆包过程中或在打包过程中设置通量的大小以及仲裁器和通量字段的开头(紧随停止位之后)。
W (width) -整个代码的宽度(以位为单位)。
比特包的完整结构如图11所示:
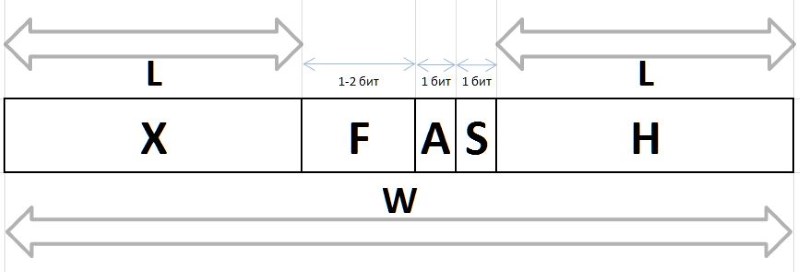
从这些链中回收的Q和R值使我们能够恢复间隔的初始值:
D = Q * 6 + R,
G =(D +1)* 2
恢复间隔的顺序使您可以通过将给定块的所有间隔依次添加到该块的给定基值(间隔的种子块)来恢复原始素数。
要使用位字符串,将使用32位整数变量,其中将处理最低有效位,使用它们后,打包时将这些位向左移动,而拆包时将其向右移动。
块状结构
除位串之外,块还包含获取或添加位以及确定块内容所必需的信息。
// // typedef unsigned char BYTE; typedef unsigned short WORD; typedef unsigned int LONG; typedef unsigned long long HUGE; typedef int BOOL; #define TRUE 1 #define FALSE 0 #define BLOCKSIZE (256) // : , #define HEADSIZE (8+8+2+2+2) // , #define BODYSIZE (BLOCKSIZE-HEADSIZE) // . // typedef struct { HUGE base; // , HUGE card; // WORD count; // WORD delta; // base+delta = WORD offset; // BYTE body[BODYSIZE]; // } crunch_block; // , put() get() crunch_block block; // . // NB: len/val rev/rel // , , // . static struct tail_t { BYTE len; // S A BYTE val; // , A - S BYTE rev; // BYTE rel; // } tails[6] = { { 4, 3, 2, 3 }, { 4, 7, 5, 3 }, { 3, 1, 0, 4 }, { 4,11, 1, 4 }, { 4,15, 3, 4 }, { 3, 5, 4, 4 } }; // BOOL put(int gap) { // 1. int Q, R, L; // (), (), int val = gap / 2 - 1; Q = val / 6; R = val % 6; L = -1; // .., 0 - 1 val = Q + 1; while (val) { val >>= 1; L++; } // L val = Q - (1 << L) + 1; // val <<= tails[R].len; val += tails[R].val; // val <<= L; // L += L + tails[R].len; // // 2. val L buffer put_index if (block.offset + L > BODYSIZE * 8) // ! return FALSE; Q = (block.offset / 8); // , R = block.offset % 8; // block.offset += L; // block.count++; // block.delta += gap; if (R > 0) // { val <<= R; val |= block.body[Q]; L += R; } // L = L / 8 + ((L % 8) > 0 ? 1 : 0); // while (L-- > 0) { block.body[Q++] = (char)val; val >>= 8; } return TRUE; } // int get_index; // // int get() { if (get_index >= BODYSIZE * 8) return 0; // int val = *((int*)&block.body[get_index / 8]) >> get_index % 8; // 4 if (val == 0) return -1; // ! int Q, R, L, F, M, len; // , , , , L = 0; while (!(val & 1)) { val >>= 1; L++; } // - if ((val & 3) == 1) // R = (val >> 2) & 1; // else R = ((val >> 2) & 3) + 2; // len = tails[R].rel; get_index += 2 * L + len; val >>= len; M = ((1 << L) - 1); // F = val & M; // Q = F + M; // return 2 * (1 + (6 * Q + tails[R].rev)); // }
增强功能
如果我们将获得的间隔基准提供给同一个7-zip存档器,则在8核服务器上进行了一个半小时的密集工作后,它将设法将输入文件压缩近5%。 即,从存档器的角度来看,在可变长度间隔的数据库中,仍然存在一些冗余。 因此,有理由在进一步减少数据冗余这一主题上进行一些猜测(从字面上看)。
素数之间的间隔序列的基本确定性使得通过一种或另一种方法进行编码效率的精确计算成为可能。 特别是,小的(而且相当混乱的)草图使得可以得出一个基本结论,即关于在三元组上编码六进制的优点,以及在可变长度的琐碎代码上所提出的方法的优点(图12):
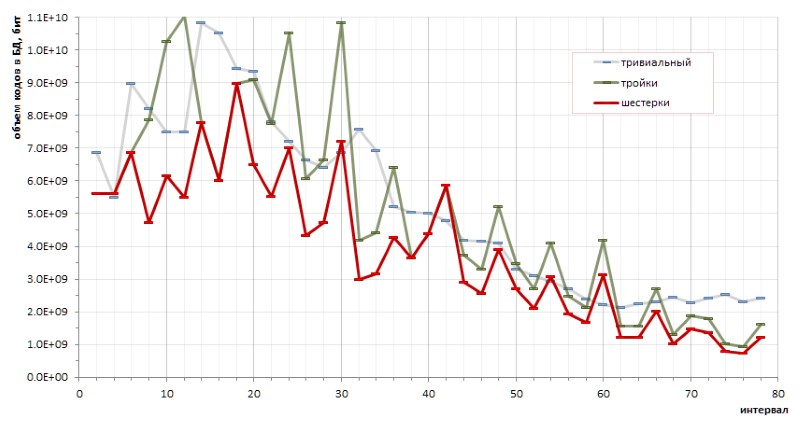
但是,红色图形的恼人高点透明地暗示可能还有其他编码方法会使图形更加柔和。
另一个方向建议检查连续间隔的频率。 从一般考虑:由于间隔6、12和18在素数总体中最常见,因此它们很可能以成对(双峰),三重(三胞胎)以及类似的间隔组合出现。 如果二元组(甚至三元组……可是突然之间!)的可重复性在间隔的总质量中具有统计学意义,那么将它们转换为一些单独的代码是有意义的。
全面实验确实揭示了个人双峰在某些方面的优势。 但是,如果预计这对(6,6)对的绝对领导地位(6,6) -所有双打的1.37%-那么该评级的其他获胜者就不那么明显了:
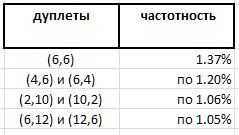
并且,由于双峰(6,6)对称的,并且所有其他注意到的双峰都是不对称的,并且在相同频率的镜像双峰的排名中都可以找到,因此该系列中双峰(6,6)的记录似乎应该在不可区分的双峰之间分成两半(6,6)和(6,6) ,这将它们带到奖金清单边界的0.68%。 这再次证实了这样的观察:关于质数的真实猜测不可能毫无意外地发生。
三胞胎的统计数据也表明了这种三重间隔的领导地位,这与间隔6、12、18的最高频率开始的推测假设并不完全吻合。按照受欢迎程度的降序,三胞胎之间的频率领导看起来如下:

等
但是,恐怕我的猜测结果对程序员的兴趣不如对数学家的兴趣,这可能是由于实践对直观的猜测进行了意外的更正。 为了进一步提高压缩率,不可能从上述频率百分比中挤出任何实质性的红利,而算法的复杂性可能会大大增加。
局限性
上面已经指出,与素数的容量有关的间隔最大值的增加非常非常慢。 特别是,从图6中可以看出,可以以64位无符号整数格式表示的任何质数之间的间隔显然将小于1600。
所描述的实现使您能够正确打包和解压缩任何18位间隔值(实际上,第一个打包错误发生在输入间隔为442358的情况下)。 我没有足够的想象力来假设素数间隔数据库可以增长到这样的值:随便它位于100位整数附近,并能更精确地计算懒惰度。 在发生火灾的情况下,有时不难扩大间隔的范围。
感谢您阅读这个地方:)