
哈Ha! 在本文中,我将讨论为Modelica中的CAE程序SimulationX创建长管道的数学模型。 使用特征方法计算液压管路中的波动过程(压力脉动,水锤等)将是一个问题。 尽管该方法已经很老了,但RuNet中没有足够的信息来说明其用于解决应用问题的应用。
在削减的基础上,我将尝试解释为什么必须考虑管道中的波动过程,以突出显示我在编程过程中遇到的问题,最后,我将对在模型中的简单长管道和URACA支架上的三柱塞高压水泵运行期间压力脉动的过程进行比较。德国。
引言
通常,在工程实践中,很少注意管道中的波动过程。 最著名的例子是水锤破坏了工程师的生命时:
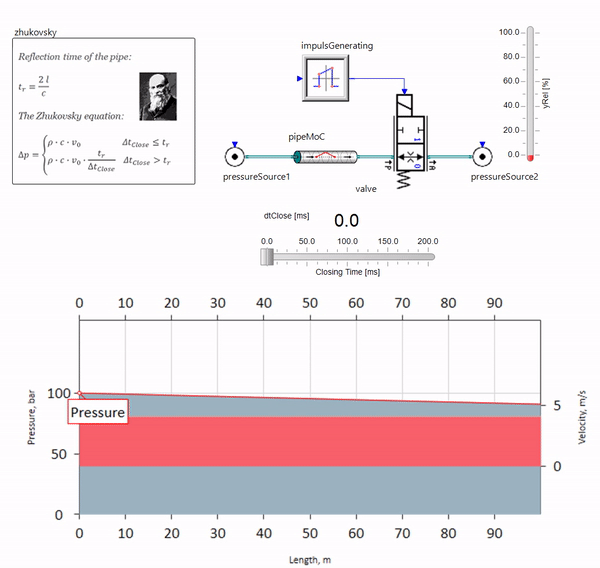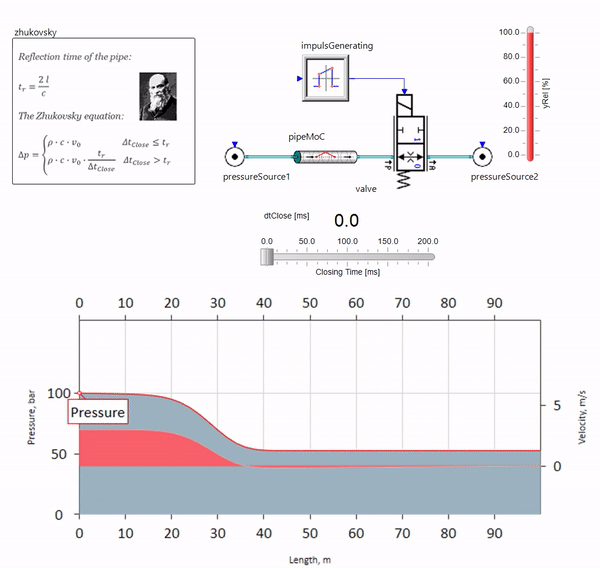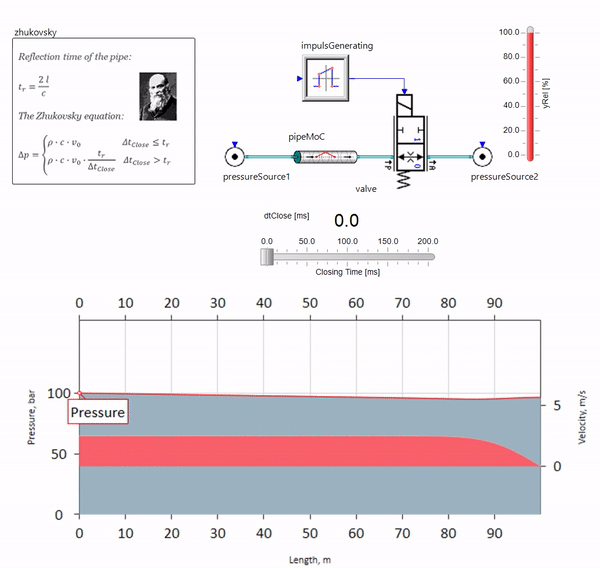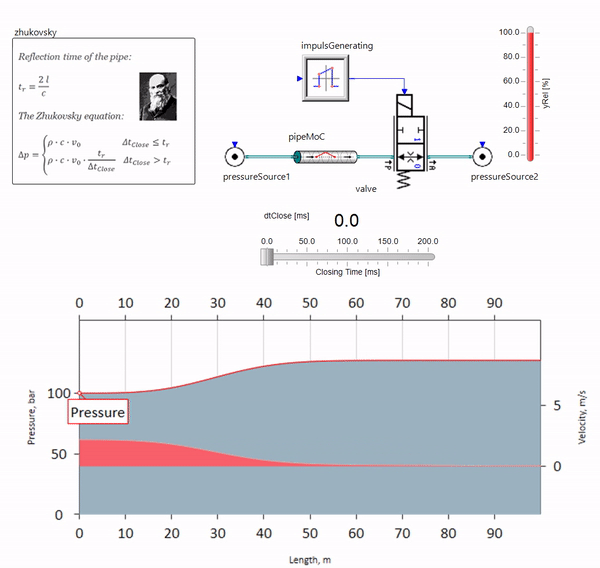
当阀门在管道末端快速关闭时,在下游,会出现压力波,该声波以声速(对于水,约为1,500 m / s)向上游移动,从恒压源反射回去,并从她这次负号。 重复此过程,直到所有的能量都消耗在摩擦上,然后直到阀门和整个管道承受冲击载荷,其振幅和频率取决于管道的长度和流体流动的初始速度。
尼古拉·朱可夫斯基(Nikolai Zhukovsky)在19世纪末描述了具有解决实际问题所必需的精度的水力喷头,从而解决了莫斯科供水系统的事故问题。 从那时起,全世界范围内用于计算阀门快速关闭时的压力跳跃的公式被称为
Zhukovsky公式 :
在实践中,水锤通常以一百米以上的管道长度表现出来。 在以下长度处,已经很难找到液压设备,其关闭速度快于从阀和阀后传递的压力波(发生水锤的条件)。 但是,如果系统具有流量脉动源(例如,带有有限数量的柱塞的容积泵),则即使相对较短的管线也仍然会破坏工程师的生命。
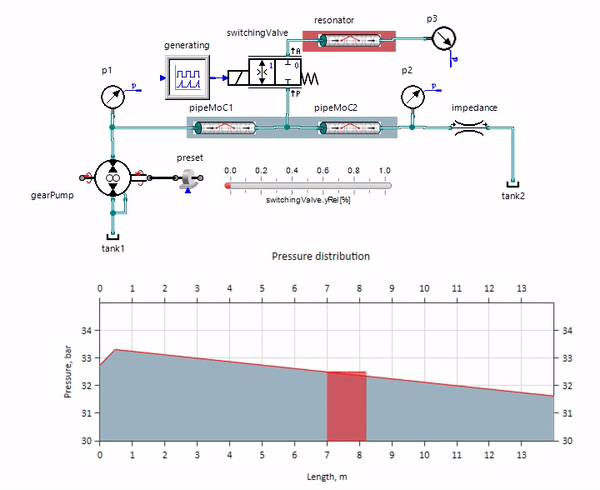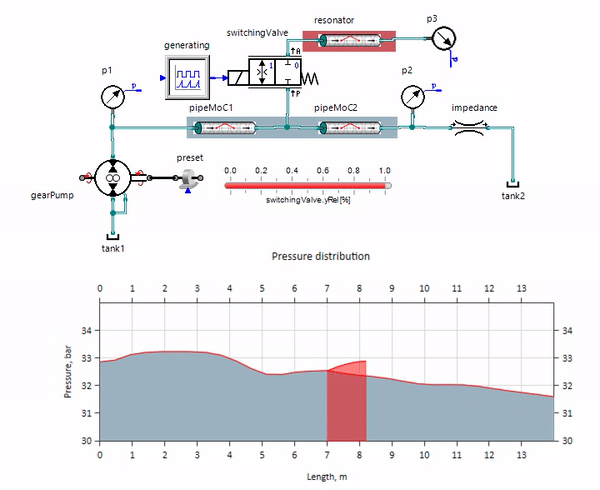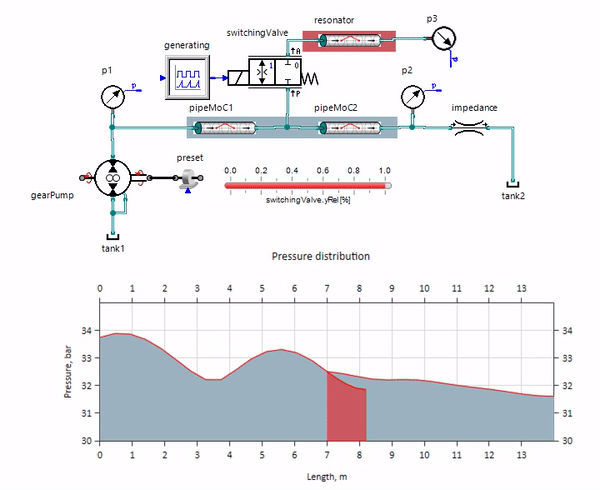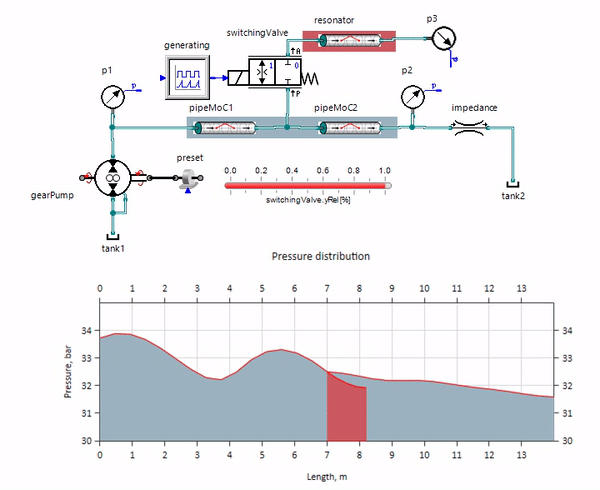
gif图像显示了一条仅超过一米长的管道的有益效果。 它的长度等于压力波长的四分之一,因此当您将其连接到主管道时,所谓的 驻波,它在反相时撞击脉动的源头,并以此方式抑制它们(这就是所谓的四分之一波脉动阻尼器)。 显然,不幸的是,在多种情况下,效果可能相反。
在我的实践中,我尝试了很长时间以消除波动过程,因为 他们的计算需要对Matan和数值方法有更深入的了解,在我的整个学习过程中,我都放纵了自己的疏忽。 但是,有一天,当我亲眼看到标准建议(将HPP,液压蓄能器随处可见,在泵入口处安排备用泵)既无助于消除工作台上的脉动,又无助于使他们更加了解过程时,我不得不更深入地研究垫子。 。 特别让我感到羞耻的是,我的研究主管已经开始为我编写C ++的管道模型。
1.分布参数中液压管路的一维模型
使由常微分方程描述的传统一维模型超出舒适区的主要问题是,即使有最恶劣的假设(最完全是充满液体,横截面长度不变,流体速度在横截面上是平均的),最简单的管道却没有传热过程由分布参数中的微分方程(欧拉方程,仅考虑第二个轴承的右侧的质量力和摩擦)来描述 avneniya):
在哪里 -密度 -速度 -压力 -摩擦损失, -重力引起的压降。即 现在集成,您不仅需要及时
而且在空间坐标上
。
对于液体,如果将方程式从保守变量重写为原始变量(速度和压力),则可以使您的生活更加简化:
在哪里 -声音的速度。现在,如果我们接受声音的速度明显大于流体运动的速度
(在没有气蚀的情况下是正确的),方程将变得更加简单:
为了解决这些方程,一种或另一种方法是摆脱空间坐标的微分
。 如果您使用有限差分方案替换空间差分,则可以正面完成此操作;对于时间而言,只需转到全差分,即在同一像元内,状态参数不取决于坐标:
现在,这些方程式可以作为常微分方程式求解,将管道的长度分成许多有限体积。 因此,例如,可以在Simscape包中,MATLAB Simulink中
完成此
操作 ,直到最近在
SimulationX中才解决了该问题。
当然可以计算出这种方式,但是这种情况下出现的数值波动受到极大的阻碍:
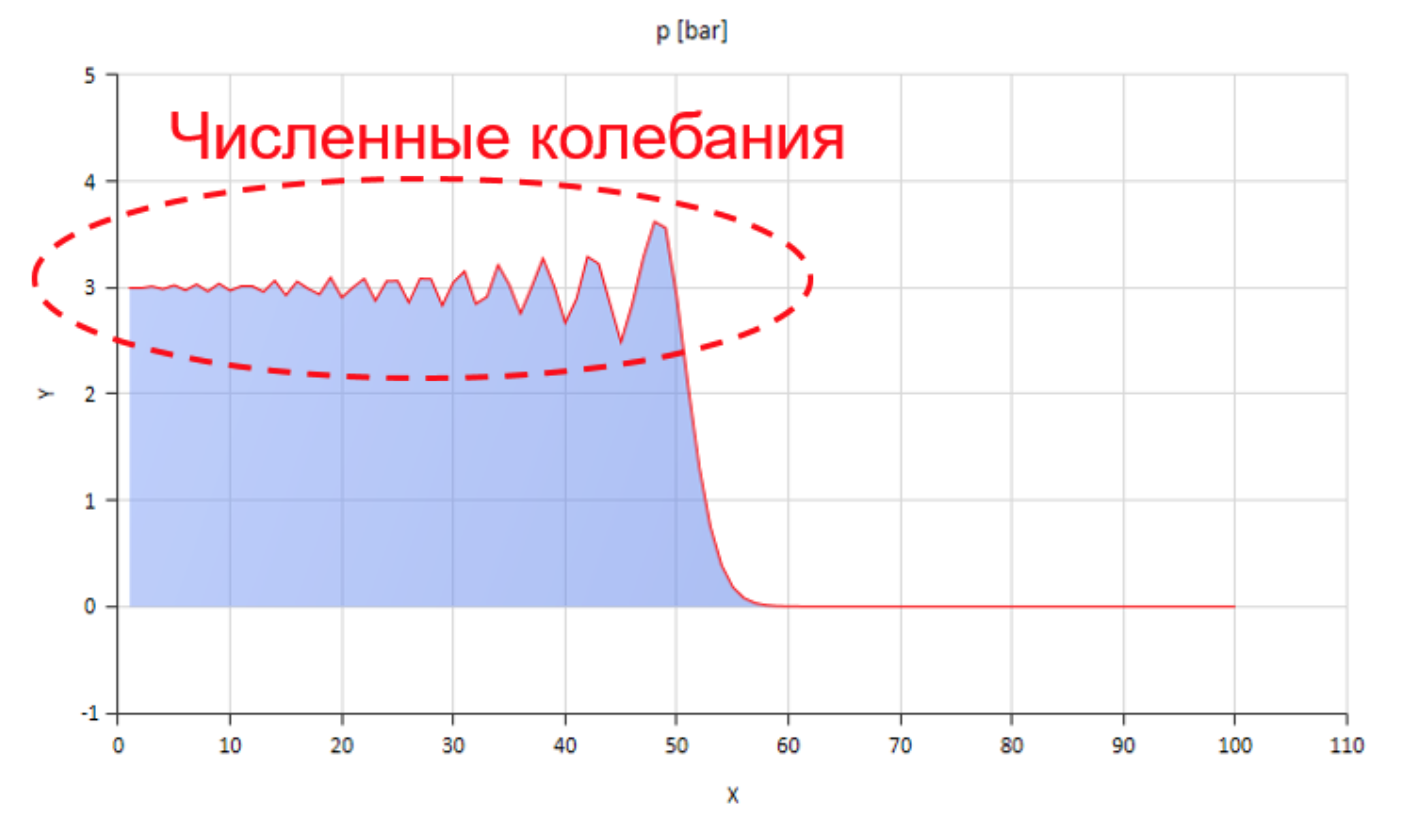 该图显示了压力波的前部从左向右移动。
该图显示了压力波的前部从左向右移动。您可以处理这些振荡,例如,引入数值扩散,但是波传播速度会明显失真。 您可以增加摩擦(特别是有助于增加其非平稳分量),但随后该模型将不再反映物理本质。
最好使用将分布参数中的方程式转换为常微分方程式的另一种方法,例如特性方法。
2.表征方法
维基百科建议“特征方法”建议:
...以找到特征,偏微分方程沿着这些特征变成一个常微分方程。 一旦找到常微分方程,就可以沿着特征对它们进行求解,并且所找到的解可以转换为原始偏微分方程的解。
它就像是哲学家的石头,但是我们没有将金属变成黄金,而是将偏微分方程变成了常微分方程,反之亦然。 问题出现了:“如何在实践中应用它?”,而且比中世纪的炼金术士更有效地...
首先,我们将理解问题陈述。 在最初的时刻,我们沿管道的长度分布有一定的压力和速度。 首先,我们将管道分成有限数量的元素,并为每个面分配一个压力值
和速度
。
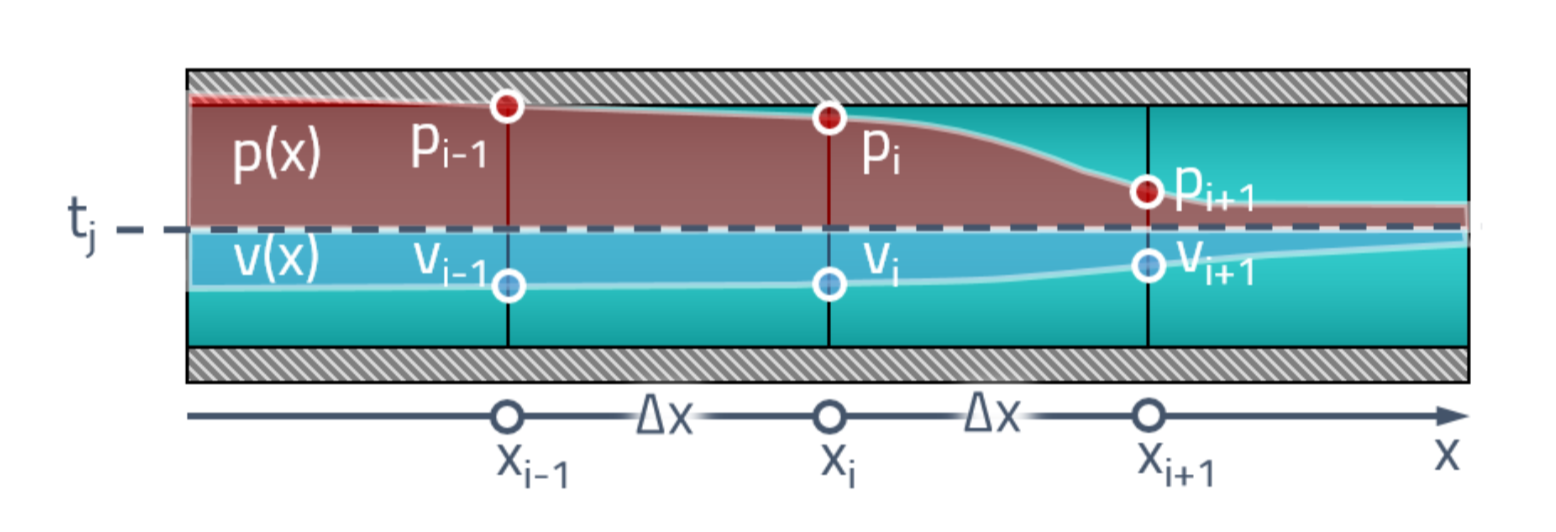
我们对这些时间点的值如何随着时间变化感兴趣
。 快进时空并将将来的管道状态置于初始状态之上:

这就是“魔术”特性派上用场的地方! 努力的农民的解释是管道中的所有变化都是以声速发生的。 当前时间点的压力和速度
取决于声波在管道中那些点的压力和速度
几秒钟前。 如下所示:

从任意一点绘制两条对称线,其斜率由声速决定。 这些正是偏微分方程转变为常微分方程的特征。 如果我们将特征与过去管道的状态相交的点命名为
和
,等式如下所示:
可以通过在网格上状态参数的值之间进行线性插值来获得这些点的压力和速度值:

重要的是要考虑到这些点应始终位于相邻的单元格之内! 为此,时间步长必须满足Courant – Friedrichs – Levy标准(CFL):
现在,至少可以将最简单的差分方案应用于这些方程式:
在由两个方程组成的系统中,两个未知数:压力
和速度
。 您可以用数字方法求解,但是没有特殊的问题可以得到解析解。 然后,如果我们接受声音速度的恒定性,就会得到一个完全明确的差分方案。
为了进行合并,我将给出一个特征方法的动画:
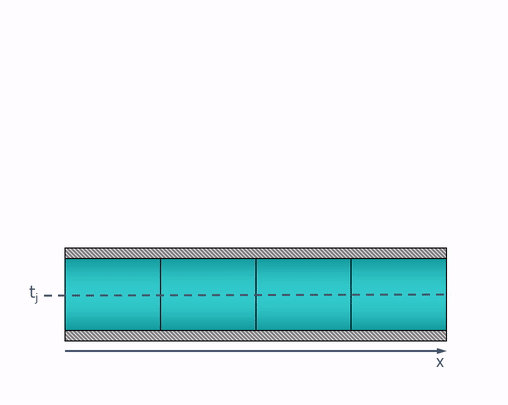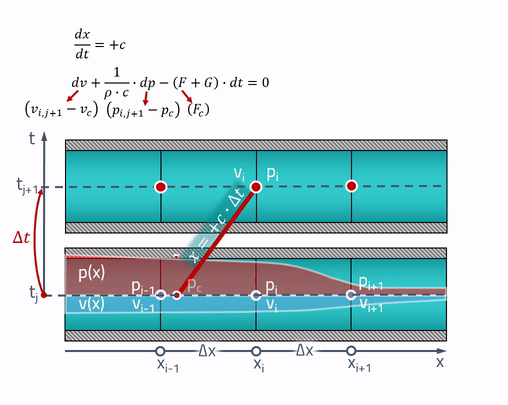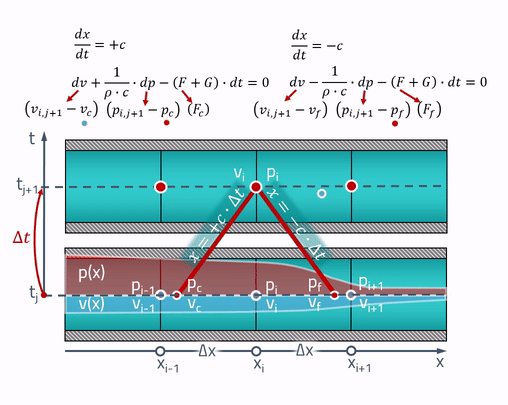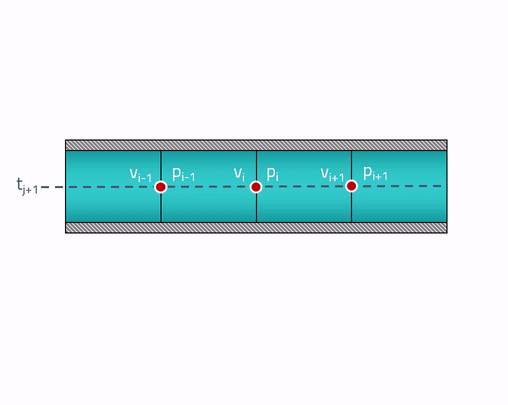
实际上......声速取决于流体压力。 在这种情况下,严格来说,该特性将不再是直线,而是要找到压力,您将需要知道声速,该速度取决于此压力。 即 该电路将已经是隐式的。
在创建模型时,我接受了这样的假设,即声速在每一步之间仅略有变化。 对于液体,在气体含量低且没有气蚀的情况下,这是正确的。 为确保结果,该模型最好在10 bar或更高的压力下使用。
3.实验
当我开始在德累斯顿的
ESI ITI GmbH工作时,我就有机会终于想到了这个模型。 一次,我在服务台收到一张票,
URACA工程师抱怨说,他们无法使用我们的“旧”管道完成实验的融合。
他们制造了高压水柱塞泵,这种泵是一个巨大的“ Karcher”,并且希望能够预测由于包括 管道中的波浪过程。 问题在于,此类泵通常只有很少的柱塞,并且以低速(250-500 rpm)运行:

因此,也由于液体可压缩性的影响,输出流量非常不均匀:

间隙和非线性使得难以在频域中对模型进行线性化和分析,并且针对此类任务的CFD计算是从麻雀处的一门大炮发射出来的。 此外,他们已经在SimulationX中建立了模型,其中考虑了泵机械部分的动力学,机架的弹性以及电动机的特性,因此,观察管道如何影响这一点将很有趣。
测试平台的布局非常简单:
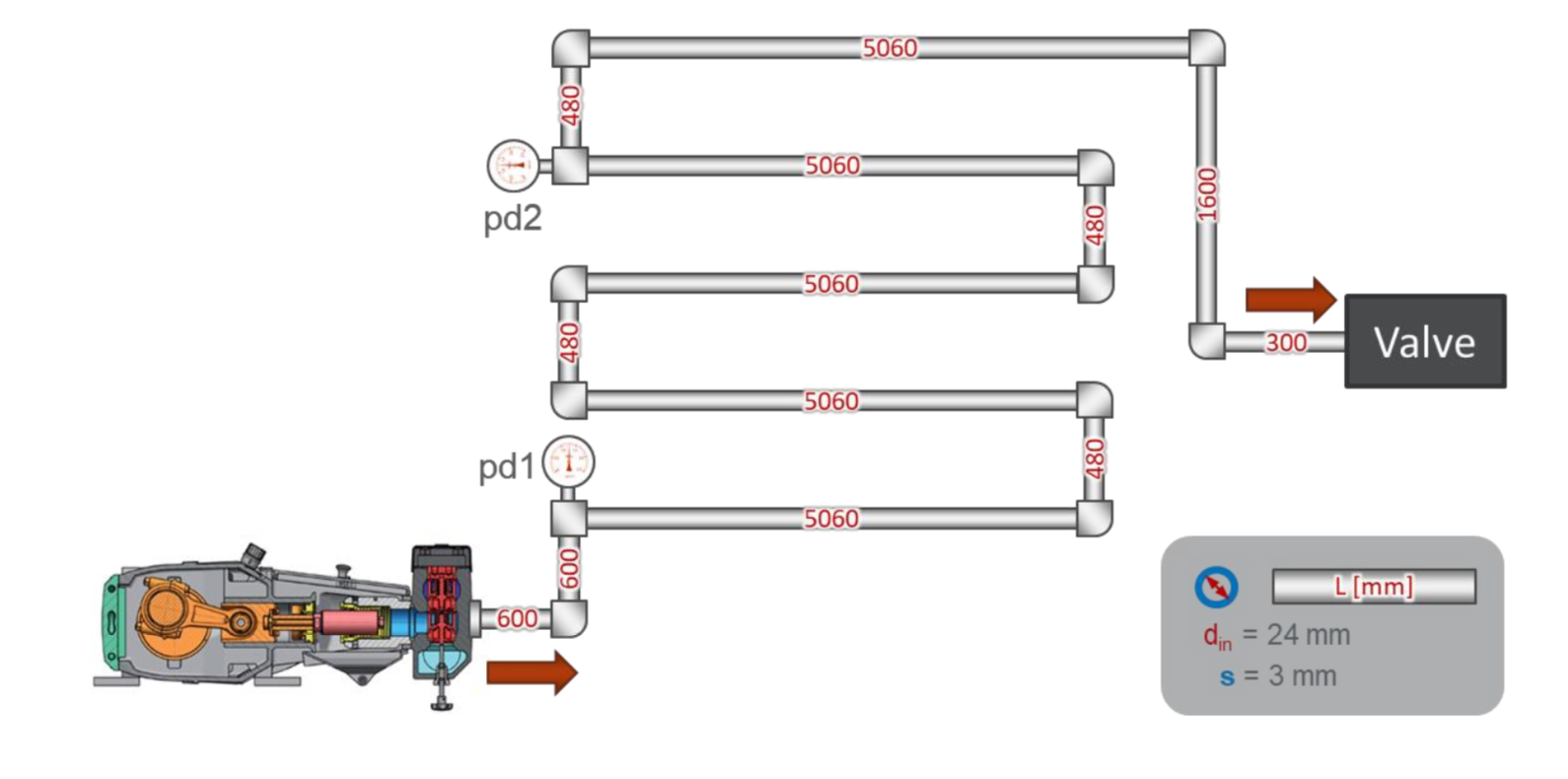
有一条简单的管道,总长度约为30米。 在管道的开始处,安装了一个距离传感器22米的压力传感器pd1-压力传感器pd2。 管道末端是一个调节系统压力的阀。
我建议测试模型的beta版本,因为在SimulationX中构建了这样的模型:
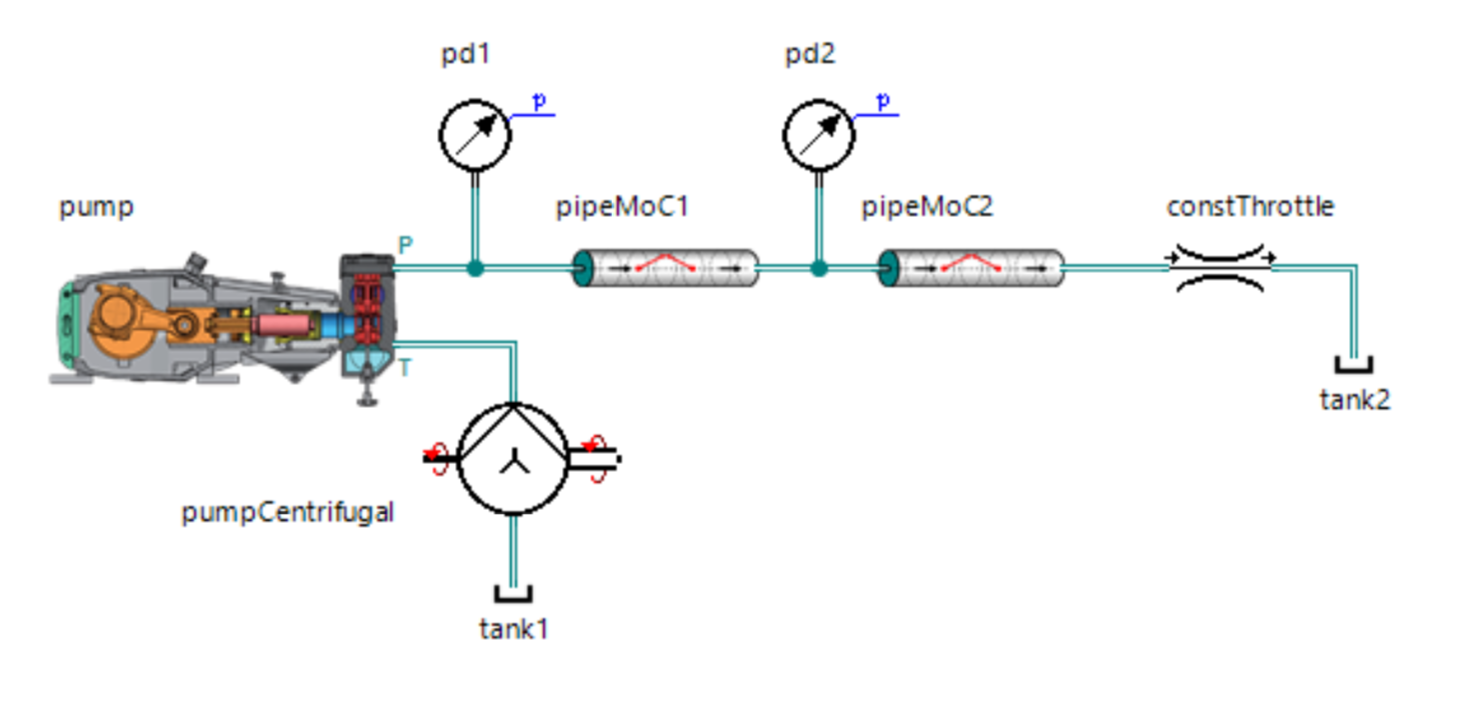
结果甚至令我惊讶:
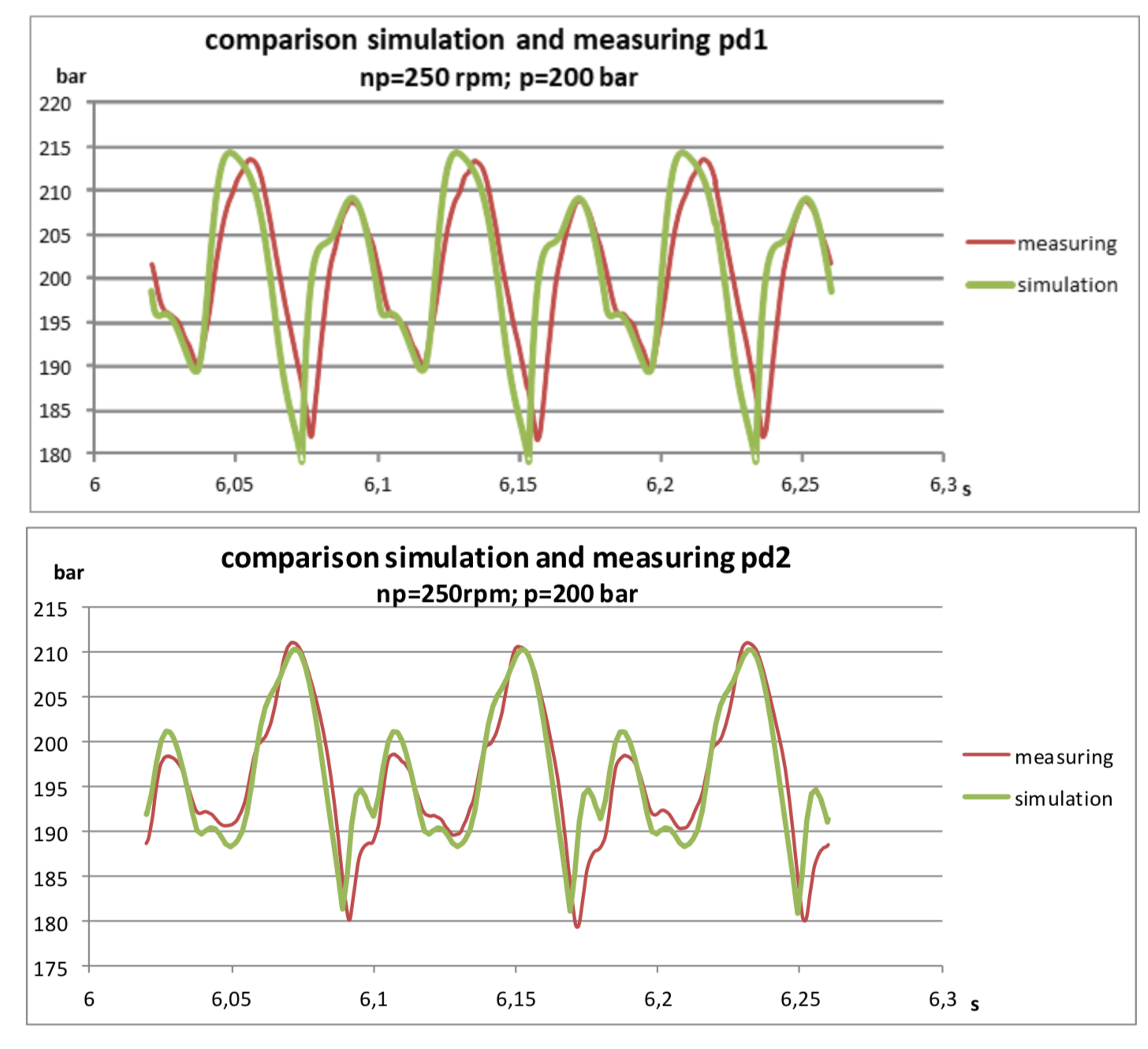
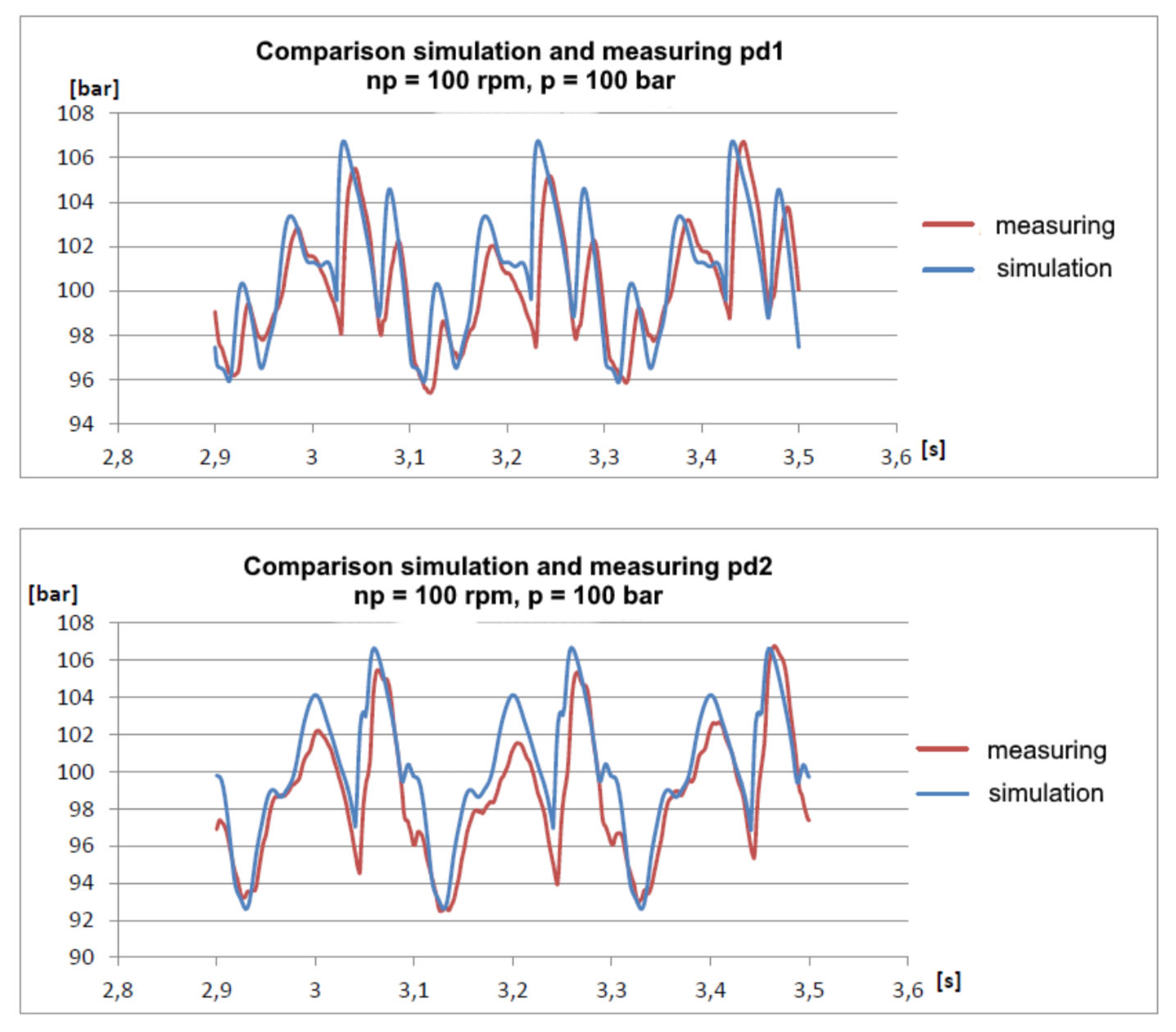
可以看出,该模型略有阻尼,只要不考虑液压阻力,这是可以理解的。 尽管如此,基波谐波的重合性非常好,并且可以以相当好的精度预测压力幅度。
这次经历使我能够在SimulationX版本中快速启动液压管路的新模型,而我陷入了这个话题,却没有注意到与学生实习生一起我如何看到了气动管路的模型,那里的一切都更加有趣。 在那里,我不得不使用基于Godunov方法的方法,该方法又基于任意不连续性衰减的Riemann问题的解决方案,好吧,这已经是另一回事了……
文学作品
- 在国内文献中,工程应用的特性方法在D. N. Popov,S。S. Panaiotti,M。V. Ryabinin。
- 在他的出版物中
高压水柱塞泵压力脉动的特征线法模拟“俄罗斯博士(马克·马克西姆·安德列夫) UweGrätz和Dipl.-Ing。 (FH)Achim Lamparter”,第11届国际流体动力大会,IFK,2018年3月19日至21日,德国亚琛,请参见PM中的文字
我更详细地研究了将特征方法与ODE的求解器耦合在一起的问题。 - 谁可以访问德国图书馆,以下论文中包含了我遇到的应用于液压线的双曲方程求解方法的最佳概述:Beck,M.,位于卡维尔捷伦登Hydraulikleitungen的Modellierung und Simulation der Wellenbewegung。 德国斯图加特,2003年。
- 一般情况下,双曲线方程式的经典: Randall J. Leveque,《双曲线问题的有限体积方法》,剑桥大学出版社,英国剑桥,2002年。