奥林匹克运动中的动态编程

你好

最近，我解决了Timus在线法官档案中的问题，并遇到了一个称为动态编程任务的部分。 我特别感兴趣这种任务，因为这种方法通常可以确保解决方案的速度和优雅。 什么是动态编程？

动态编程是一种解决问题的方法，其中将子任务划分为与原始任务相比“更简单”的子任务。 “动态”一词的含义与“归纳”非常接近：假定答案因某种含义而为人所知 $$$k$ ，而我想找到答案 $$$k + 1$ 。 在数学中，这称为归纳转换，是动态编程的主要思想。

简单的例子

最引人注目的指示性任务是计算任务 $$$n$ 斐波那契数列的编号。 已知该序列具有以下属性：

$$

$$F_0 = F_1 = 1，\ F_n = F_ {n-1} + F_ {n-2}$$

这立即意味着递归公式：

int Fibonacci(int n) { if(n == 1 || n == 2) return 1; return Fibonacci(n-1) + Fibonacci(n-2); } 

如果递归从“末尾”寻找数字，则以下方法顺序计算位于之间的所有数字 $$$0$ 和 $$$n$ ：

 int dpFibonacci(int n) { int prev1 = 1; int prev2 = 1; int curr = 0; for(int j = 2; j < n; j++) { curr = prev1 + prev2; prev1 = prev2; prev2 = curr; } return curr; } 

显然，对于足够大 $$$n$ 该算法的运行速度更快：它不会多次计算中间值。 考虑一个稍微复杂的例子。

示例1.您正在收费楼梯上行走。 踩 $$$我$ 您必须支付的步骤 $$$a_i$ 硬币。 您可以转到下一步或跳过一个步骤。 任务：通过 $$$n$ 并花费尽可能少的硬币。

显然，在每一步中，我们将“付款”的数量减至最少，但我们可能会遇到一个非常昂贵的步骤，我们希望避免这样做。 创建一个值数组 $$$d$ 在其中 $$$j$ -第一位将是要花费的（最少）硬币数量 $$$j$ 第一步。 立即清楚的是 $$$d_1 = a_1，\ d_2 = a_2$ 。 然后，我们将至少执行前两个步骤，并增加该步骤本身的成本：

$$

$$d_i = \最小\左（d_ {i-1}，d_ {i-2} \右）+ a_ {i}$$

我们稍微改变了问题的条件：假设在某些步骤中您可以获得硬币（这意味着 $$$a_k <0$ ） 算法中需要更改哪些内容才能给出正确的结果？


考虑另一个使用“二维”动力学的示例。

例子2.在迷宫里有 $$$n \乘以m$ 房间，每个房间都装有金（放在笼子里 $$$（i，j）$ 谎言 $$$a_ {ij}$ 金）。 任务是确定从某个点出发的最佳路线可以收集的最大黄金量 $$$（0,0）$ 到这一点 $$$（n，m）$ 如果您可以向下或向右移动。

因此，我们想知道通往细胞的最佳途径 $$$（i，j）$ 。 我们可以从两个单元格到达这里- $$$（i-1，j）$ 和 $$$（i，j-1）$ 。 假设这两个单元格的最佳路由是已知的（它们存储在某个表中） $$$d$ ），那么该单元格的答案 $$$（i，j）$ 获得如下：

$$

$$d_ {ij} = \ max \ left（d_ {i-1j}，d_ {ij-1} \ right）+ a_ {ij}$$

这是另一种经典的动态编程任务，其修改在体育编程任务中非常普遍。 此处将详细解释类似的任务。

更具挑战性的任务

如果需要，可以在任何需要的地方使用动态方法。 考虑Timus在线法官档案中的一项任务 。

问题的数学公式如下：需要找到将给定数量分解为完整平方所需的最小项数。

和以前一样，假设我们知道所有数字的答案 $$$k-1$ 存储在某个数组中 $$$d$ 我们想找到 $$$d_ {k}$ 。

拿这个号码 $$$k$ 并分析可能的情况：

1. $$$k$ 是一个完整的正方形。 在这种情况下 $$$d_ {k} = 1$ 。
2. 也许以前的数字 $$$k-1$ 是一个完整的正方形。 然后 $$$d_ {k} = d_ {k-1} + 1$ 。

通常，将单元添加到上一个单元的选项似乎还不错。

我们进行如下操作：我们寻求分解 $$$k = q ^ 2 + s$ 这样

$$

$$d_ {q ^ 2} + d_s <d_ {k-1} +1。$$

由于 $$$q ^ 2$ -然后全角 $$$d_ {q ^ 2} = 1$ 和

$$

$$d_s <d_ {k-1}，$$

也就是说，我们发现一个分区比 $$$d_ {k-1} + 1$ ，在这种情况下，答案将是

$$

$$d_k = d_ {s} + d_ {q ^ 2} = d_s +1。$$

考虑以下问题 。 目标是从 $$$N$ 根据规则的多维数据集：

1. 楼梯至少有两个台阶；
2. 楼梯不能有两个相同的台阶；
3. 楼梯的台阶按升序排列（即，下一个台阶大于上一个台阶）。

这次我们将建立二维动力学。 建立表格 $$$d$ 在哪个位置 $$$（i，j）$ 组成的楼梯数量 $$$我$ 高度不超过立方体 $$$j$ 。 如果解决了，那么我们问题的答案将是总和

$$

$$\ sum \ limits_ {j = 1} ^ n d_ {nj}$$

因此，我们将解决寻找由 $$$我$ 高的立方体 $$$j$ 。 图为落入楼梯 $$$d_ {74}$ ：

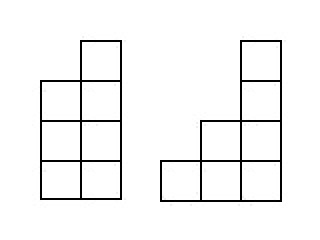
由于我们知道所有楼梯，其中包含较少的立方体，因此我们将“拆分”楼梯 $$$（i，j）$ 右列。 结果是楼梯c $$$i-j$ 多维数据集。 范例 $$$i = 9，\ j = 4$ ：

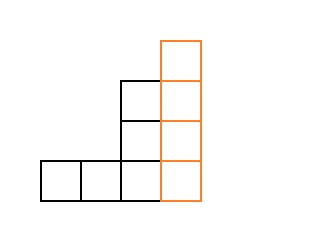
但是对于这样的楼梯，结果是已知的，因此我们将以一个循环对所有这些楼梯进行排序 $$$k$ 并将所有结果相加。 这样

$$

$$d_ {ij} = \总和\ limits_ {k = 1} ^ {j-1} d_ {i-jk}$$

现在我们将对楼梯的高度进行排序：

$$

$$d_ {ij} = \总和\ limits_ {k = 1} ^ {j-1} d_ {i-jk}，\ j = \上线{1，i}$$

最后，改变 $$$我$ 来自 $$$1$ 之前 $$$n$ 我们得到了答案。

重要提示 ：在建立矩阵的过程中，必须考虑到 $$$d_ {ii} = 1$ ，因为否则某些类型的楼梯会“丢失”（“断开”时），但是不用说，这样的楼梯不能满足问题的条件，因此答案将是数字 $$$d_ {nn}-1$ 。


使用一维数组解决下一个任务 。

所以我们有。 第一个耳语会识2个单词。 每个ent教他自己知道的两个ent的所有单词：Young和Old。 反过来，年轻人被教了许多他已经知道的单词，而老年人只被教了一个单词。 您需要知道多少个实体确切知道 $$$K$ 词（有必要以模数推论这些实体的数量 $$$P$ ）

解决方案非常简单。 创建一个数组 $$$d$ 在其中 $$$我$ -我们将存储ents的数量（模 $$$P$ ）谁知道 $$$我$ 话。 这一切都始于第一个输入项，它知道两个词，因此 $$$d_2 = 1$ 。 然后一切都很简单：

• 所有知道奇数单词的ents都是古老的，只能从先前的单词中学习。 因此奇怪 $$$i：\ d_i = d_ {i-1};$
• 至于只知道偶数个字词的人，都是从精灵那里得到相同数量字词的人（年轻） $$$+$ 从先前（旧）中学到的那些人； 也就是说，即使 $$$我$ 我们有 $$$d_i = d _ {{i \反斜线2}} + d_ {i-1}$ 。

它仍然需要处理计算模。 为了不存储大量数字，我们将立即记住所有取模值。


使用的资源：

1. Timus在线法官；
2. 关于动态编程的一些知识；
3. 比较属性取模。