引言
最常见的椭圆型方程是泊松方程。
许多数学物理学问题都简化为该方程式的解，例如，固体中的静态温度分布问题，扩散问题，存在电荷的非导电介质中的静电场分布问题以及许多其他问题。
为了在多次测量的情况下求解椭圆方程，使用数值方法将微分方程或其系统转换为代数方程组。 解决方案的准确性取决于计算机的坐标网格步骤，迭代次数和位网格[1]。
该出版物的目的是获得Dirichlet和Neumann边界条件的Poisson方程的解，并通过实例研究解的松弛方法的收敛性。
泊松方程是指椭圆型方程，在一维情况下，其形式为[1]：
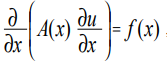
（1）
其中x是坐标； u（x）是所需的函数； A（x），f（x）是一些连续的坐标函数。
我们针对情况A = 1求解一维泊松方程，在这种情况下，其形式为：
（2）
在间隔[xmin，xmax]上，我们定义一个统一的坐标网格，步长为Δ：
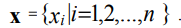
（3）
所考虑问题的第一类边界条件（狄利克雷条件）可以表示为：
（4）
其中x1，xn是区域[xmin，xmax]的边界点的坐标； g1，g2-一些
常数。
考虑中的问题的第二种边界条件（Neumann条件）可以表示为：
（5）
使用有限差分法在均匀坐标网格（3）上离散Dirichlet边界条件，我们得到：
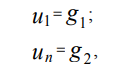
（6）
其中，u1，un是分别在点x1，xn处的函数u（x）的值。
离散网格上的Neumann边界条件（3），我们得到：
（7）
对于内部网格点，离散化方程（2），我们得到：
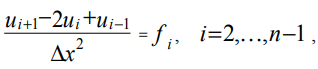
（8）
其中ui，fi是坐标为xi的网格点处的函数u（x），f（x）的值。
因此，作为离散化的结果，我们获得了一个维数为n的线性代数方程组，其中包含n-2个方程，其形式为区域内部点的（8）以及两个边界点的方程（6）和（7）[1]。
以下是在网格（3）上具有边界条件（4）-（5）的方程（2）的数值解的Python列表。
上市解决方案from numpy import* from numpy.linalg import solve import matplotlib.pyplot as plt x0=0
我们得到：
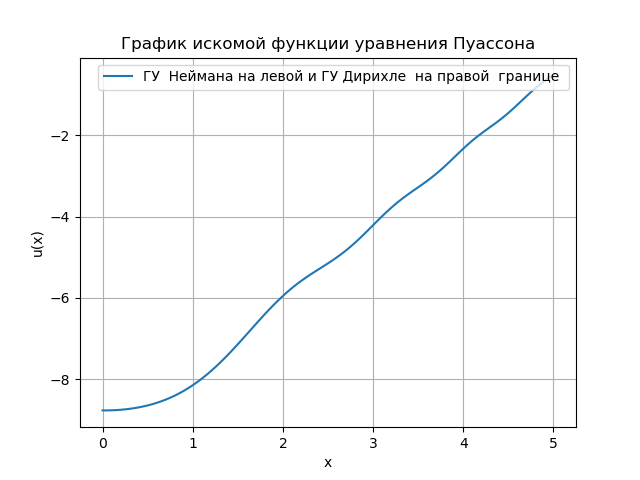
我用Python开发的程序便于分析边界条件，上述Python解决方案算法使用Numpy函数-u = linalg.solve（a，bT）.T求解代数方程组，从而提高了平方矩阵{a}的速度。 但是，随着测量数量的增加，有必要切换到使用三个对角矩阵，即使对于非常简单的任务，其解决方案也很复杂，我在论坛上找到了一个示例：
具有三个对角矩阵的解决方案示例 from __future__ import print_function from __future__ import division import numpy as np import time ti = time.clock() m = 1000 A = np.zeros((m, m)) B = np.zeros((m, 1)) A[0, 0] = 1 A[0, 1] = 2 B[0, 0] = 1 for i in range(1, m-1): A[i, i-1] = 7 A[i, i] = 8 A[i, i+1] = 9 B[i, 0] = 2 A[m-1, m-2] = 3 A[m-1, m-1] = 4 B[m-1, 0] = 3 print('A \n', A) print('B \n', B) x = np.linalg.solve(A, B)
对流扩散方程在网格Dirichlet问题各个方向上均匀性的数值解程序
[2]
（9）
对流项和迭代松弛方法使用中心差的近似值，对于f（x）= 1和6（x）= 0.10的问题的数值解，收敛速度对松弛参数的依赖性。 在网格任务中：
（10）
我们将矩阵A表示为对角矩阵，下三角矩阵和上三角矩阵的总和：
（10）
松弛方法对应于迭代方法的使用 ：
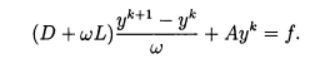
（11）
在
说说上放松，什么时候
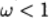
-放松一下。
程序清单 from numpy import * """ - . .""" def relaxation(b, f, I1, I2, n1, n2, omega, tol = 1.e-8): h1 = I1 / n1 h2 = I2 / n2 d = 2. / h1**2 + 2. / h2**2 y = zeros([n1+1, n2+1]) ff = zeros([n1+1, n2+1]) bb = zeros([n1+1, n2+1]) for j in arange(1,n2,1): for i in arange(1,n1,1): ff [i,j] = f(i*h1, j*h2) bb[i,j] = b(i*h1, j*h2)
）
我们得到：
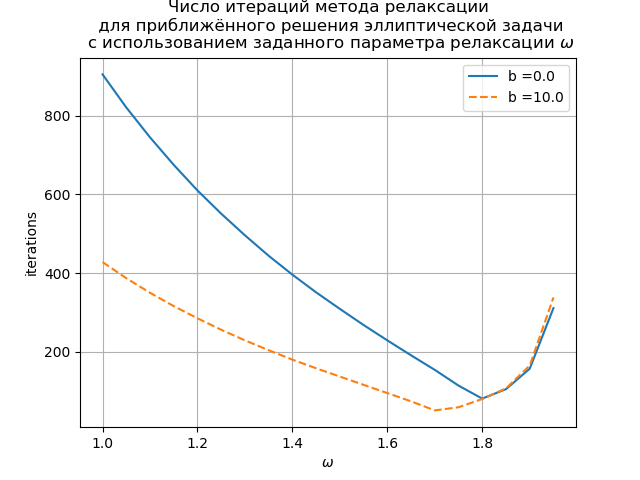
该图显示了迭代次数对Poisson方程（b（x）= 0）和对流扩散方程（b（x）= 10）的弛豫参数的依赖性。 对于泊松网格方程，通过解析求出松弛参数的最佳值，并且迭代方法收敛于
。
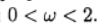
结论：
- 使用设置边界条件的灵活系统在Python中解决椭圆问题
- 结果表明，松弛法具有最佳范围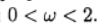（ ）松弛参数。
参考文献：
- Ryndin E.A. 解决数学物理问题的方法。 -塔甘罗格：
TRTU出版社，2003年。-120页。 - Vabishchevich P.N.数值方法：计算车间。 -M .：书屋
Librocom，2010年-320羽。