学校教科书I中的任务

第一部分
第二部分
第三部分

考虑一下“ 5至15岁儿童的任务”一书中针对问题38的算法解决方案

计算金额：

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$$

（错误不超过答案的1％）

以下是在drRacket的 Scheme （Lisp）中计算此系列的部分和的算法（drRacket允许您以普通分数执行计算）：

#lang racket (define series_sum ( lambda (n) (if (= n 0) 0 (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1))) ) ) ) (series_sum 10) (series_sum 100) (series_sum 1000) (series_sum 10000) (series_sum 100000) (series_sum 1000000) (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* n (+ n 1.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 10) (series_sum_1 100) (series_sum_1 1000) (series_sum_1 10000) (series_sum_1 100000) (series_sum_1 1000000) 

最后两个示例drRacket计算出错误



该程序可以在ideide.com和codepad.org上运行。



如果我们考虑普通分数的部分和，我们可以看到级数的和是

$$

$$\ frac {n} {n + 1}$$

让我提醒你 $$$\ lim \ frac {n} {n + 1} = \ frac {1} {1+ \ frac {1} {n}} = \ frac {1} {1} = 1$ 在 $$$n \至\ infty$

微分与积分学课程363（4）的第二卷考虑了一般情况

$$

$$\ sum \ frac {1} {（\ alpha + n）（\ alpha + n +1）} = \ frac {1} {\ alpha + 1}$$

“开发人员数学” 课程中 的任务 ：
查找序列中的成员数 $$$\ frac {2n-1} {4n + 5}$ 躺在间隔之外 $$$（1- \ frac {1} {1000}； 1+ \ frac {1} {1000}）$

让我们继续本文的主题。

让我们考虑一本问题书中的另一个示例。
43 。 兔子数（斐波纳契数），形成一个序列 $$$（a_ {1} = 1），1、3、5、8、13、21、34，...，$ 在其中 $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ 给大家 $$$n = 1，2，...$ 。 找到最大的公约数除数 $$$a_ {100}$ 和 $$$a_ {99}$ 。

答案：两个相邻的斐波那契数是互质数，即 $$$\ gcd（u_ {n + 1}，u_ {n}）= 1$
（gcd是最大的公约数，即GCD）。

“书中的证明”，超出数学教科书的范围” [10-11]


在下一个任务中，您需要计算黄金分割率 ， $$$\ frac {\ sqrt {5} + 1} {2} \约1,618$ 。 [这是明信片的长宽比，在切开一边为明信片较小边的正方形时，仍保持相似。]

53 。 对于斐波那契数列 $$$a_ {n}$ 任务43找到关系的极限 $$$\ frac {a_ {n + 1}} {a_ {n}}$ 在努力的同时 $$$n$ 到无穷大：

$$

$$\ frac {a_ {n + 1}} {a_ {n}} = 2，\ frac {3} {2}，\ frac {5} {3}，\ frac {8} {5}，\ frac { 13} {8}，\ frac {21} {13}，\ frac {34} {21}。$$

考虑代表该系列两个相邻成员之间差异的细分 $$$\ frac {a_ {n + 1}} {a_ {n}}$ 。

甚至该系列的成员 $$$\ frac {a_ {n + 1}} {a_ {n}}$ 代表一个不断增长的序列 $$$x_ {n}$

$$

$$\ frac {3} {2}，\ frac {8} {5}，\ frac {21} {13}，...，$$

奇数行成员 $$$\ frac {a_ {n + 1}} {a_ {n}}$ 代表递减顺序 $$$y_ {n}$

$$

$$2，\ frac {5} {3}，\ frac {13} {8}，...，$$

通过嵌入的间隔引理（微分和积分学课程，38）

$$

$$c = \ lim x_ {n} = \ lim y_ {n}$$

对于我们在某一时刻的行 $$$c$ 公平平等 $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = \ frac {a_ {n + 1}} {a_ {n}}$

划分 $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ 在 $$$a_ {n + 1}$ 我们得到方程式 $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = 1 + \ frac {a_ {n}} {a_ {n + 1}}$ 。
通过更换 $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = x，\ frac {a_ {n}} {a_ {n + 1}} = \ frac {1} {x}$ 我们得到二次方程 $$$x = 1 + \ frac {1} {x}$ 。

如果在geogebra程序中我们将点2和 $$$\ frac {3} {2}$ ， $$$\ frac {3} {2}$ 和 $$$\ frac {5} {3}$ ， $$$\ frac {5} {3}$ 和 $$$\ frac {8} {5}$ 等 -得到一个相似的数字




通常，在Python中有一种用于计算斐波纳契数的标准算法。
该算法在Python.org上可用

 def fib(n): a, b = 0, 1 while a < n: print(a) a, b = b, a+b fib(100) 

您可以检查链接
更改此算法，以使其打印出近似黄金分割率。 对于两个相邻的数字a和b，我们将a + b的总和除以b

 def fib(n): a, b = 0.0 , 1.0 while a < n: print((a+b)/b) a, b = b, a+b fib(100) 

您可以检查链接

这是SICP教程中有关黄金分割率的一些任务。


下面的示例来自任务书“ 5至15岁儿童的任务”
54 。 计算无限连续分数

$$

$$1 + \ frac {1} {2 + \ frac {1} {1+ \ frac {1} {2+ \ frac {1} {1+ \ frac {1} {2 + ...}}}}}$$

UPD 考虑方程式

$$

$$\ alpha = 1+ \ frac {1} {2 + \ frac {1} {\ alpha}}$$

根据《数论》一书中的定理236和235：

$$

$$\ alpha = \ frac {P_ {1} \ alpha + P_ {0}} {Q_ {1} \ alpha + Q_ {0}}$$

我们组成一个价值表 $$$P_ {n}$ 和 $$$Q_ {n}$ 在 $$$n = 0,1：$



这样 $$$\ alpha = \ frac {3 \ alpha + 1} {2 \ alpha + 1}，2 \ alpha ^ {2}-2 \ alpha -1 = 0$

由于 $$$\ alpha> 0，$ 然后

$$

$$\ alpha = \ frac {1 + \ sqrt {3}} {2}$$

考虑一下“数学课本后面”一书中的问题[10-11]
4 。 显示该号码 $$$\ sqrt {1+ \ sqrt {1 + \ sqrt {1 + ...}}}$ 等于数字 $$$\ varphi$ 定义黄金分割率。

考虑选项 $$$x_ {n} = \ sqrt {c + \ sqrt {c + ... + \ sqrt {c}}}$
微分与积分的过程，35（2）

这样 $$$x_ {n + 1}$ 从...获得 $$$x_ {n}$ 根据公式

$$

$$x_ {n + 1} = \ sqrt {c + x_ {n}}$$

...根据主定理，选项 $$$x_ {n}$ 有一定的限制 $$$一$ 。 为了确定它，我们将等式传递到极限

$$

$$x_ {n + 1} ^ {2} = c + x_ {n};$$

我们以这样的方式 $$$一$ 满足二次方程

$$

$$a ^ {2} = c + a$$

这个等式的根源不同。 但是我们感兴趣的极限 $$$一$ 不能为负，因此，它恰好等于正根：

$$

$$a = \ frac {\ sqrt {4c + 1} + 1} {2}$$

从中我们可以得出结论，“黄金比例”是方程的解 $$$a ^ {2} = c + a$
在 $$$c = 1$ 。


此外，在微分和积分学课程35（3）中，考虑了用于计算逆数的算法

让 $$$c$ 是任何正数，并放入 $$$x_ {n} = cy_ {n}$ 。 上面写的递归关系将被替换为：

$$

$$y_ {n + 1} = y_ {n}（2-cy_ {n}）$$

取初始值 $$$y_ {0}$ 在以下条件下： $$$0 <y_ {0} <\ frac {1} {c}$ 我们明白了 $$$y_ {n}$ 单调增加，往往会 $$$\ frac {1} {c}$ 。 根据此方案，在计数机上，计算逆数 $$$c$ 。

逆数计算算法 $$$c$ 在Python中：
（ Ideone.com和codepad.org ）

 def reciprocal(c,y0,n): arr=[] for i in range(n): arr.append(y0) y0=y0*(2-c*y0) return arr 

倒数功能以数字作为输入 $$$c$ 初始值 $$$y_ {0}$ ，迭代次数 $$$n$ 并返回数字的“近似值”数组 $$$\ frac {1} {c}$ 。
$$$y_ {0} = 0.1$ 在 $$$c <10$
$$$y_ {0} = 0.01$ 在 $$
$$$y_ {0} = 0.001$ 在 $$$100 <c <1000$
等
互惠函数如何在各种情况下工作的示例 $$$c$

 >>> reciprocal(3,0.1,10) 

[0.1、0.17、0.2533、0.31411733000000003、0.3322255689810133、0.3333296519077525，
0.3333333332926746、0.3333333333333333337、0.3333333333333333337、0.33333333333333337]

 >>> reciprocal(8,0.1,10) 

[0.1、0.12、0.1248、0.12499968、0.1249999999991808、0.125、0.125、0.125、0.125、0.125]

 >>> reciprocal(5,0.1,10) 

[0.1，0.15000000000000002，0.18750000000000003，0.19921875000000003，0.19999694824218753，0.1999999999534339，0.20000000000000004，0.19999999999999998，
0.19999999999999998、0.19999999999999998]

几何解释

让我们尝试使用切线法来近似反数。
切线 $$$y = f'（x_ {0}）（x-x_ {0}）+ f（x_ {0}）$ 功能图 $$$y = \ frac {1} {x}$ 用公式表示 $$$y = \ frac {2} {x_ {0}}-\ frac {x} {x_ {0} ^ {2}}$

替换数字 $$$1,2,3,4，...$ 代替 $$$x_ {0}$ 我们得到切线方程

$$

$$y = 2-x$$

$$

$$y = 1- \ frac {x} {4}$$

$$

$$y = \ frac {2} {3}-\ frac {x} {9}$$

$$

$$y = \ frac {1} {2}-\ frac {x} {16}$$

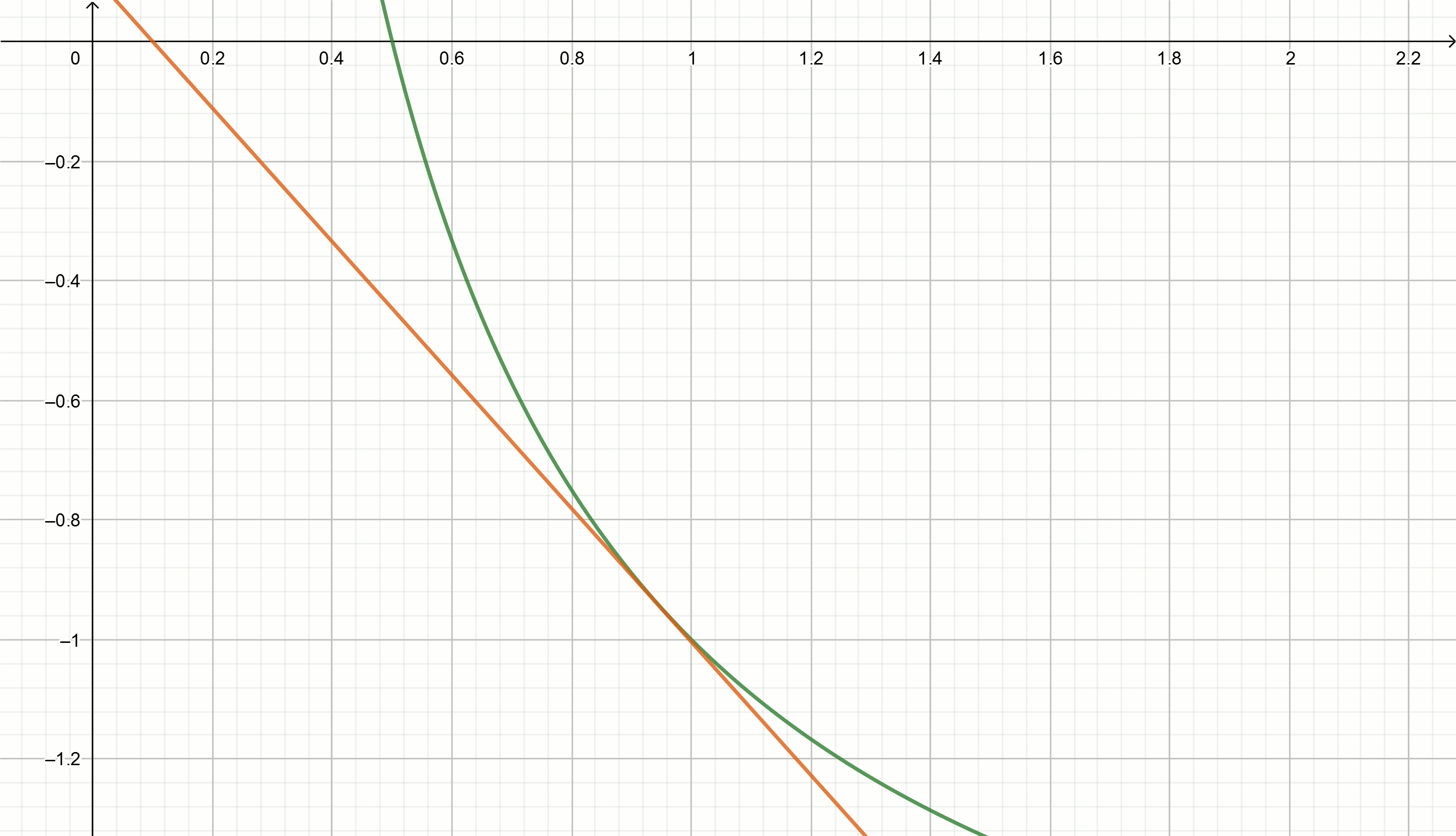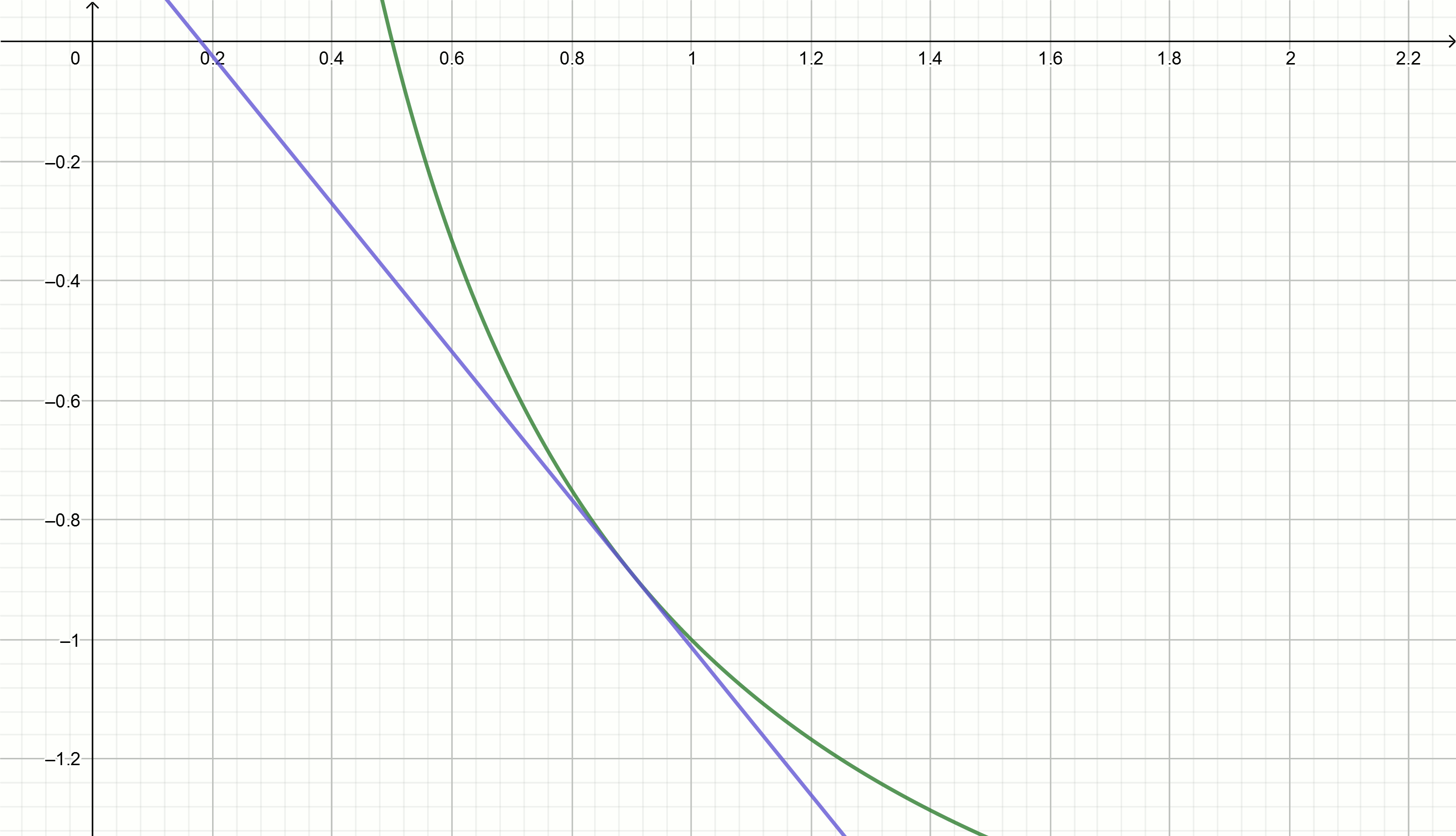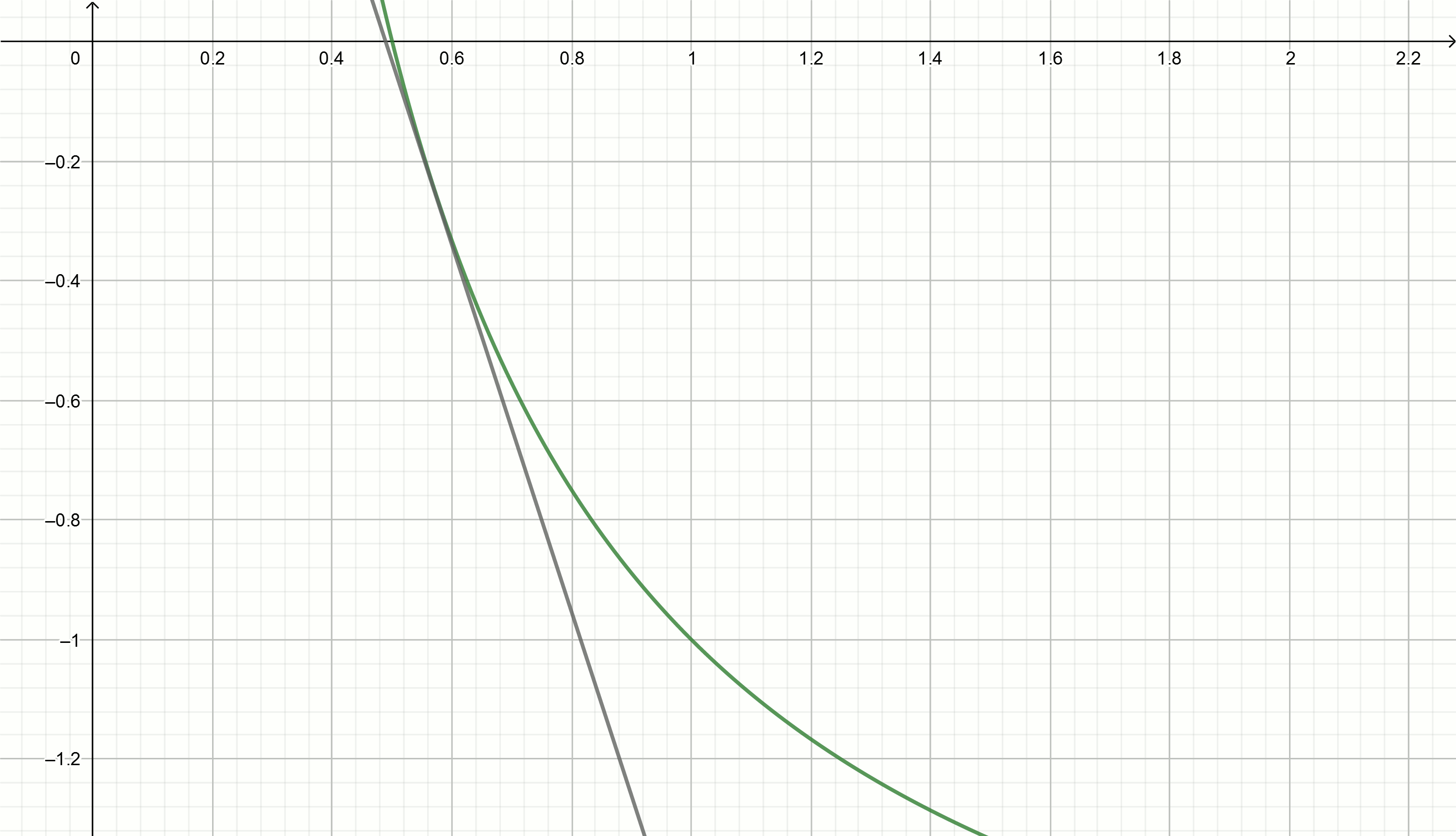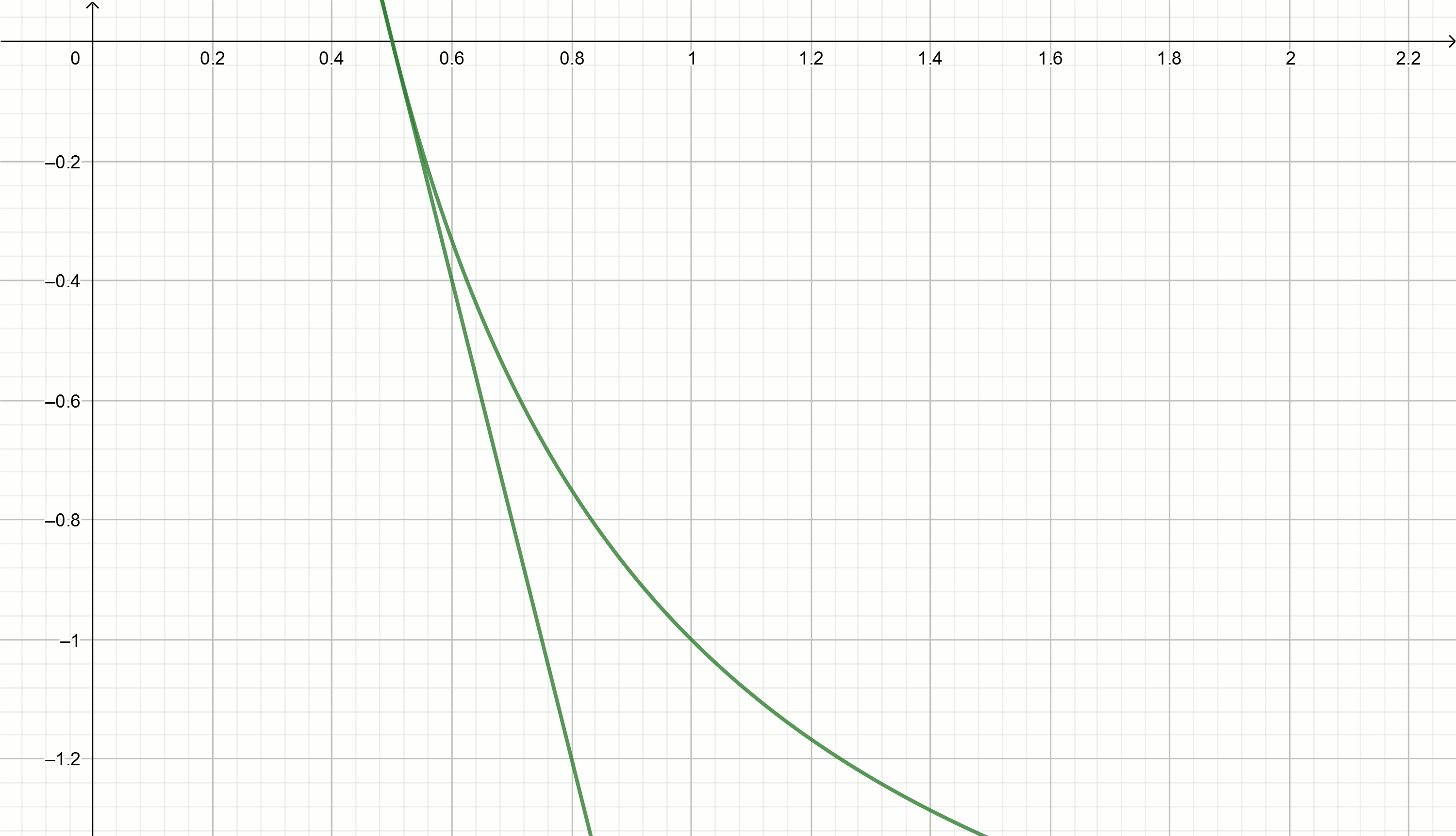
建立这些图


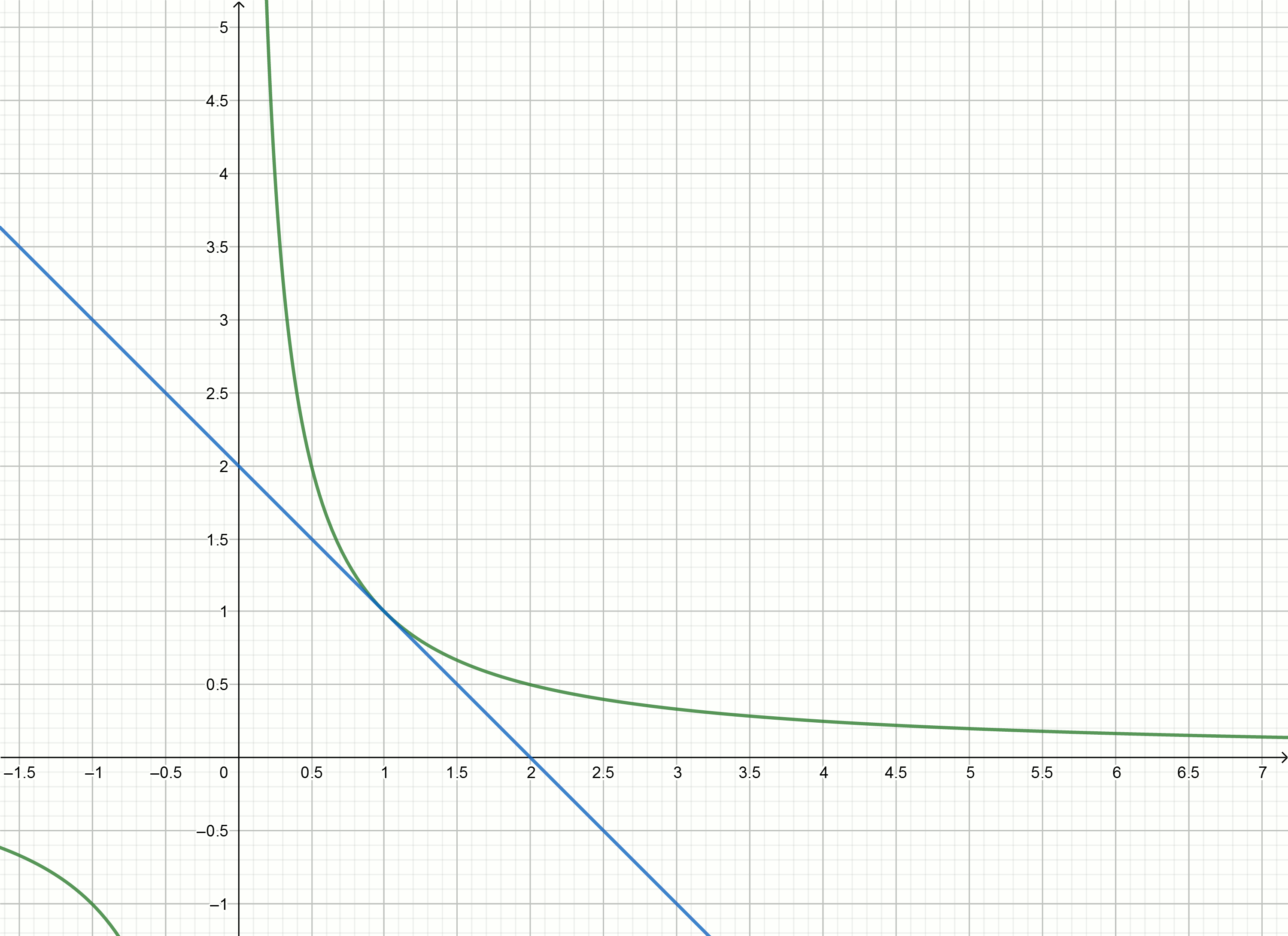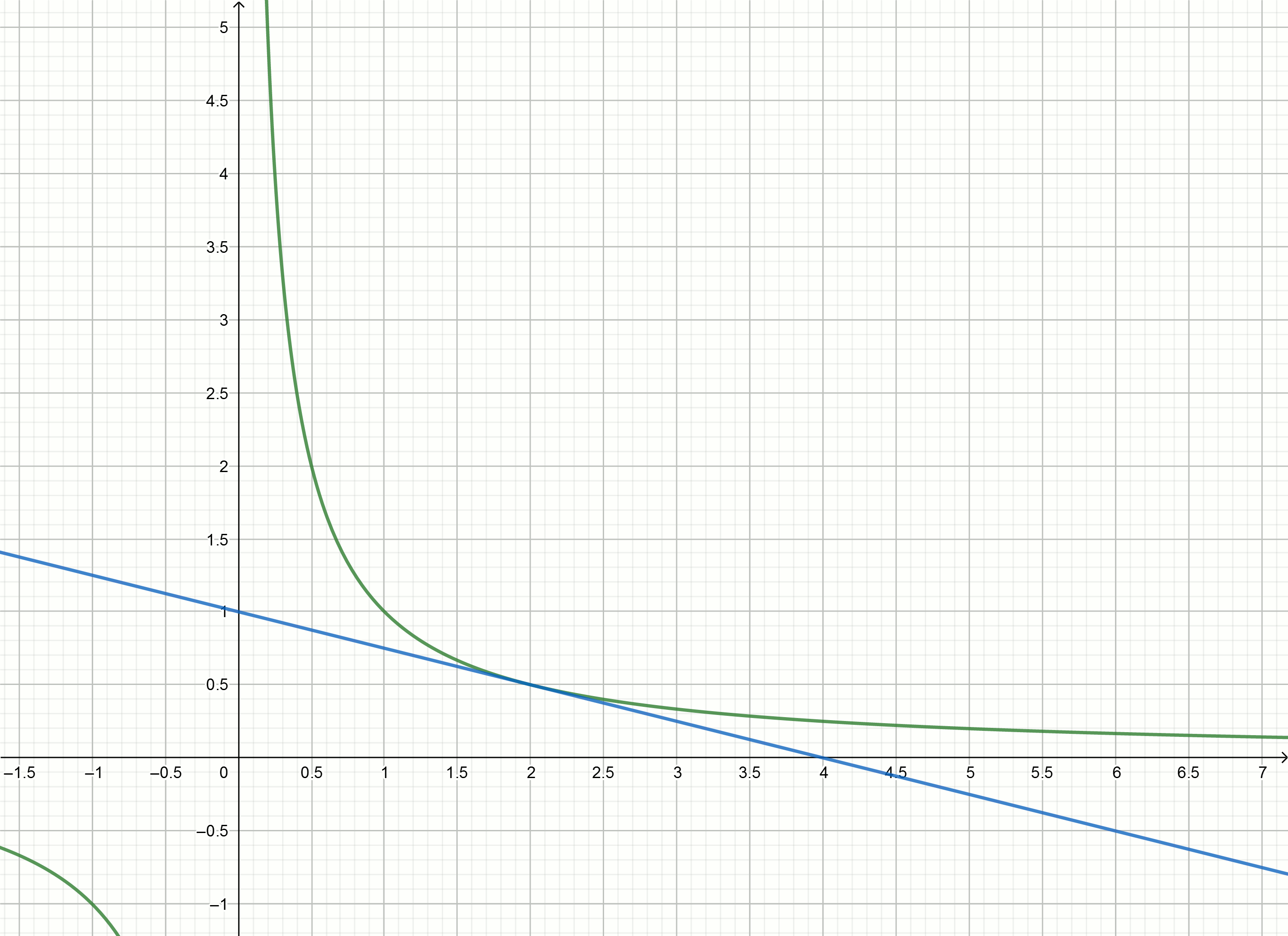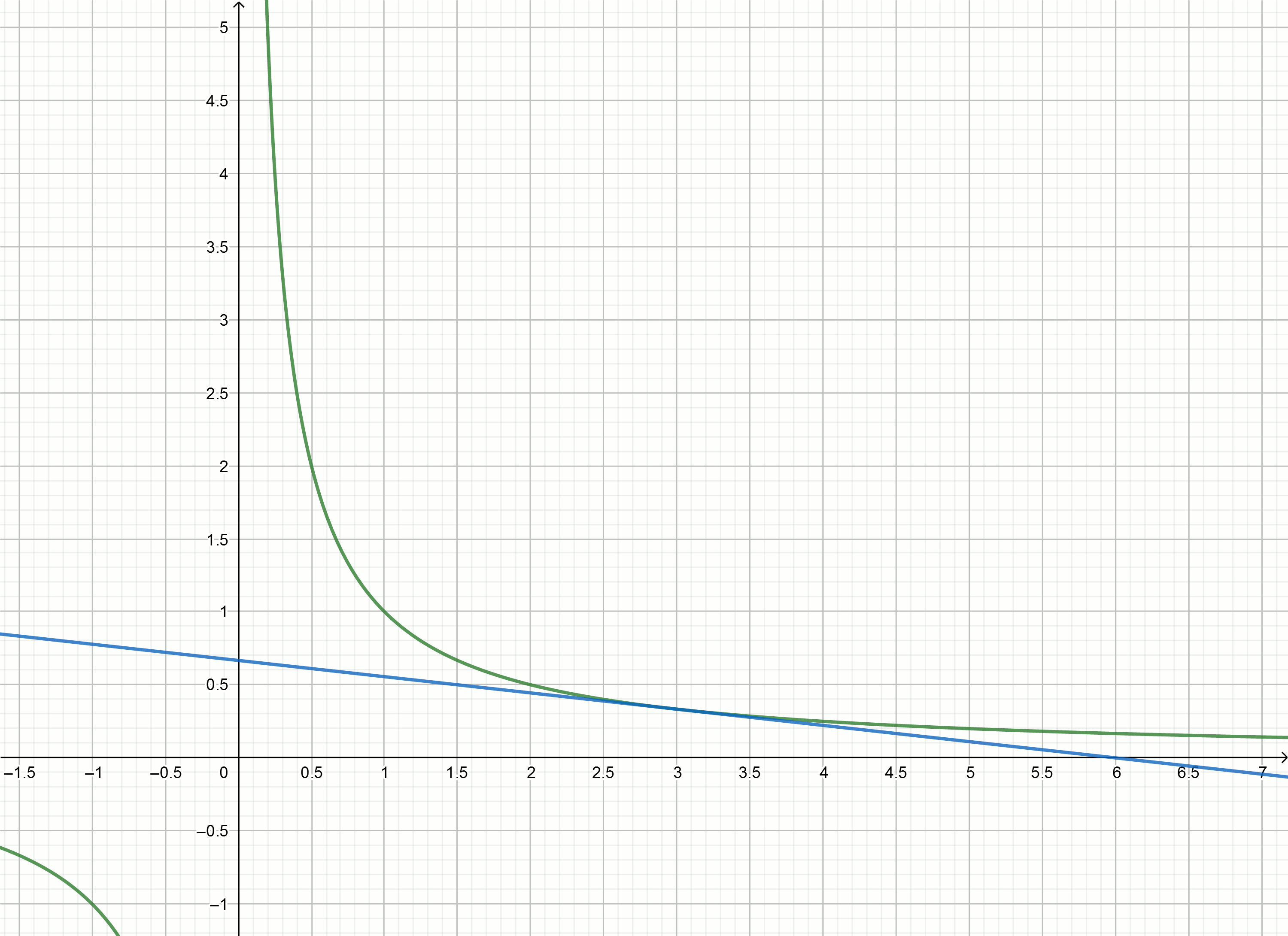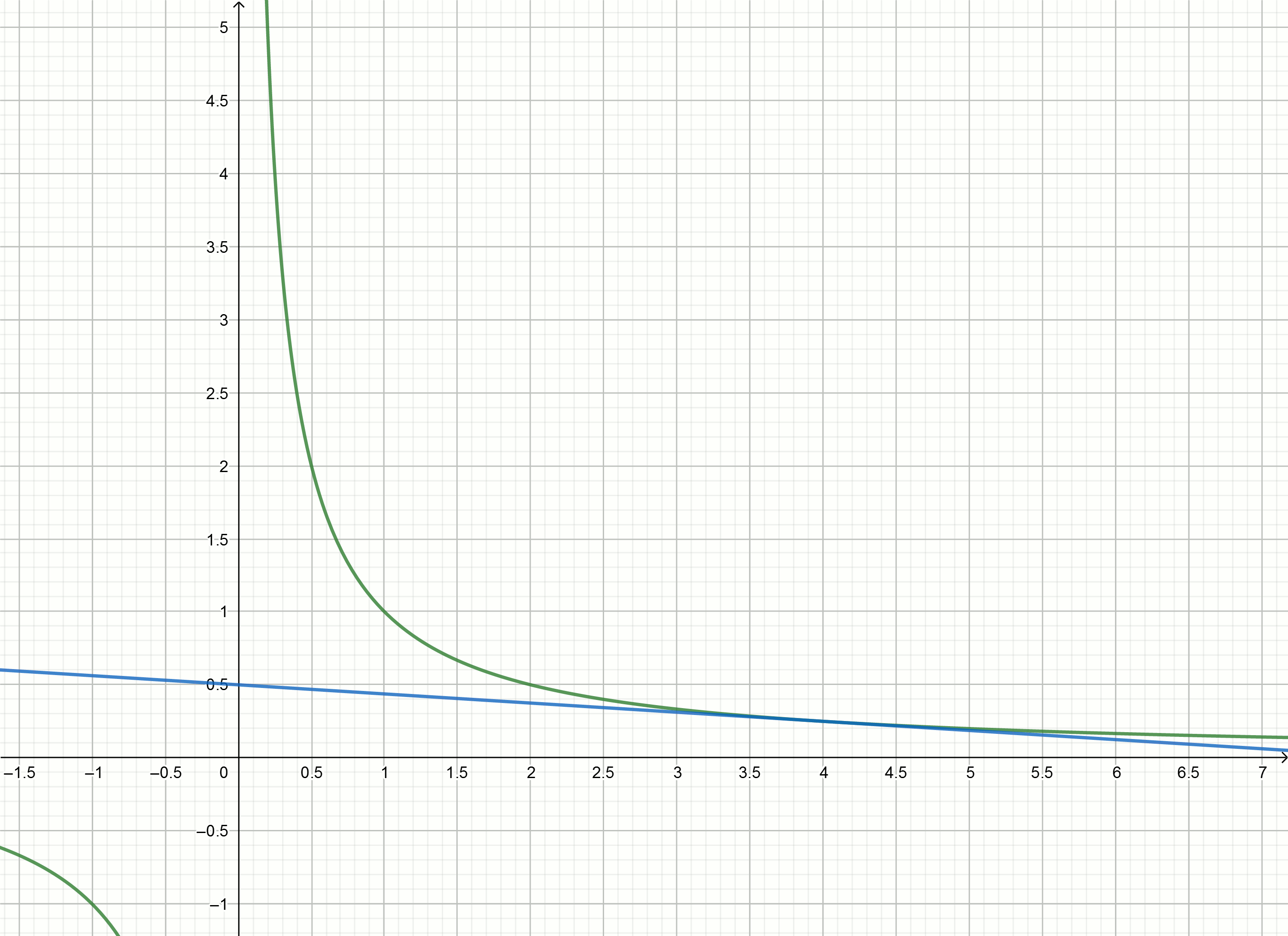
如果将双曲线下移到 $$$\ alpha$ 然后它越过横坐标 $$$\ frac {1} {\ alpha}$ 。
切线方程转换为 $$$y = \ frac {2} {x_ {0}}-\ frac {x} {x_ {0} ^ {2}}-\ alpha$
此外，将切线的方程式等于​​零并表示 $$$x$ 我们得到方程式 $$$x = x_ {0}-\ frac {f（x_ {0}）} {f'（x_ {0}）}$

相反 $$$f（x_ {0}）$ 替代品 $$$\ frac {1} {x_ {0}}-\ alpha$
相反 $$$f'（x_ {0}）$ 替代品 $$$-\ frac {1} {x_ {0} ^ {2}}$

我们得到表达 $$$x = x_ {0} +（\ frac {1} {x_ {0}}-\ alpha）x_ {0} ^ {2}$
扩大括号，我们得到 $$$x = x_ {0} + x_ {0}-\ alpha x_ {0} ^ {2}$

代替 $$$0.1$ 进入方程式 $$$x = x_ {0}（2- \ alpha x_ {0}）$ 并查看哪些值将“运行” $$$x$ 在 $$$\ alpha = 2$ 我们得到 $$$0.1、0.18、0.29、0.42、0.49、0.5$

将这些值代入方程式 $$$y = \ frac {2} {x_ {0}}-\ frac {x} {x_ {0} ^ {2}}-2$ 我们得到直接

$$

$$y = 0.111-\ frac {x} {0.897}$$

$$

$$y = 0.222-\ frac {x} {0.81}$$

$$

$$y = 0.816-\ frac {x} {0.504}$$

$$

$$y = 0.857-\ frac {x} {0.49}$$

$$

$$y = 1.5-\ frac {x} {0.326}$$

$$

$$y = 2-\ frac {x} {0.25}$$

平方根提取

回到非理性表达式，我们考虑一种提取平方根的迭代方法。
我们将使用Heron迭代方法编写算法

$$

$$x_ {n + 1} = \ frac {1} {2}（x_ {n} + \ frac {a} {x_ {n}}）$$

 def square_root(a,n): # a -  , n -   x0=1 #    1 arr=[] for i in range(n): arr.append(x0) #      x0=0.5*(x0+a/x0) #      return arr print square_root(2,10) 

codepad.org

使用Rafael Bombelli使用的连续分数计算平方根

寻找价值 $$$\ sqrt {n}$ ，首先我们定义其整体近似值： $$$\ sqrt {n} = a \ pm r$ 在哪里 $$$0 <r <1$ 。 然后 $$$n =（a \ pm r）^ {2} = a ^ {2} \ pm 2ar + r ^ {2}$ 。 从这里很容易推断出 $$$r = {\ frac {| n-a ^ {2} |} {2a \ pm r}}$ 。 在公式中替换结果表达式 $$$\ sqrt {n} = a \ pm r$ ，我们得到了连续的分数扩展：

$$

$$a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}$$

因此，我们可以编写使用分解成连续分数的平方根提取算法

 def square_root(n,a,n_count): # n- , a -    x0=a #    a arr=[] for i in range(n_count): #       a arr.append(x0-a) #  a x0=2*a+(na*a)/x0 return arr print square_root(2.0,1.0,10) 

codepad.org

通常，实数和复数以及一个或多个变量的功能可以是私有分子和分母。
提取整数部分的方法允许以无穷连续分数的形式表示无理数，其分子为单位（频繁的分子等于1）。
这是一个连续小数扩展的例子 $$$\ sqrt {5}$ 摘自《代数》一书

$$

$$\ sqrt {5} -2 = \ frac {（\ sqrt {5} -2）（\ sqrt {5} +2）} {\ sqrt {5} +2} = \ frac {1} {\ sqrt { 5} +2}$$

这样 $$$\ sqrt {5} = 2+ \ frac {1} {\ sqrt {5} +2}$

选择数字的整数部分 $$$\ sqrt {5} +2：E（\ sqrt {5} +2）= 4$ 。 均值 $$$\ sqrt {5} +2$ 可以表示为 $$$4 + \ alpha$ 。 很明显 $$$\ alpha = \ sqrt {5} + 2-4 = \ sqrt {5} -2$ 因此 $$$\ sqrt {5} + 2 = 4 + \ sqrt {5} + 2$ 。 再次，我们消除第二项分子中的非理性：

$$

$$\ sqrt {5} -2 = \ frac {1} {\ sqrt {5} +2}$$

结果是：

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}$$

让我们执行另一个类似的步骤：

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}}$$

容易看出，在该示例中，将整个部分分离出来并形成连续部分的过程没有止境。 在每个新分母中都会出现 $$$4$ 和期限 $$$\ sqrt {5} -2$ 。 因此，很明显 $$$\ sqrt {5}$ 表示为无限的连续分数：

$$

$$\ sqrt {5} = [2，4，4，4，...]$$

假说

如果 $$$d \ in \ mathbb {N}，\ sqrt {d} \ notin \ mathbb {N}$ 然后是数字的连续分数 $$$\ sqrt {d} + [\ sqrt {d}]$ 纯粹是周期性的。
Evarist Galois证明了这一假设。

即 如果是分数的非周期部分 $$$[1; 2,2,2，...] = \ sqrt {2}$ 添加整个部分 $$$[\ sqrt {2}] = 1$ 那么我们得到一个纯周期性的分数 $$$[2,2,2，...]$ 。

$$$\ sqrt {3} = [1; 1,2，...];$
$$$\ sqrt {3} +1 = [2,1，...]$

$$$\ sqrt {5} = [2; 4,4,4，...];$
$$$\ sqrt {5} +2 = [4,4,4，...]$

$$$\ sqrt {6} = [2; 2,4，...];$
$$$\ sqrt {6} +2 = [4,2，...]$

$$$\ sqrt {13} = [3; 1,1,1,1,6，...];$
$$$\ sqrt {13} +3 = [6,1,1,1,1,1，...]$


如果在根中按照Bombelli方法分解

$$

$$\ sqrt {n} = a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ { 2} |} {2a \ pm \ cdots}}}}}}}$$

添加到第一学期 $$$一$ ，我们得到一个纯周期性分数

$$

$$\ sqrt {n} + a = 2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}}$$

剩下的是使分数变成更熟悉的形式（分子中包含单位）。
将分数的分子和分母除以 $$$| n-a ^ {2} |$ 我们得到表达

$$

$$\ sqrt {n} + a = 2 a \ pm {\ frac {1} {\ frac {2a} {| na ^ {2} |} \ pm {\ frac {1} {2a \ pm {\ frac { 1} {\ frac {2a} {| na ^ {2} |} \ pm \ cdots}}}}}}}$$

这样

$$

$$\ sqrt {2} +1 = 2+ \ frac {1} {\ frac {2} {1} + \ frac {1} {2 + \ frac {1} {\ frac {2} {1} +。 ..}}} = [2,2,2，...]$$

$$

$$\ sqrt {3} +1 = 2+ \ frac {1} {\ frac {2} {2} + \ frac {1} {2 + \ frac {1} {\ frac {2} {2} +。 ..}}} = [2,1，...]$$

$$

$$\ sqrt {5} +2 = 4+ \ frac {1} {\ frac {4} {1} + \ frac {1} {4 + \ frac {1} {\ frac {4} {1} +。 ..}}} = [4,4,4，...]$$

$$

$$\ sqrt {6} +2 = 4+ \ frac {1} {\ frac {4} {2} + \ frac {1} {4 + \ frac {1} {\ frac {4} {2} +。 ..}}} = [4,2，...]$$

$$

$$\ sqrt {13} +3 = 6+ \ frac {1} {\ frac {6} {4} + \ frac {1} {6 + \ frac {1} {\ frac {6} {4} +。 ..}}} = [6，\ frac {3} {2}，...]$$

我们将编写一个程序来计算连续分数近似值 $$$[6，\ frac {3} {2}，...]$

 #lang racket (define continued_fraction ( lambda (n) (if (= n 0) 1 (+ 6 (/ 1 (+ 3/2 (/ 1 (continued_fraction(- n 1)))))) ))) (continued_fraction 4) 

codepad.org
在第四步中，我们得到 $$$6 \ frac {3818} {6305}$ 等于 $$$6.60555114 ...$ 一会儿 $$$\ sqrt {13} +3 \大约6.60555127$ 。




PS解决问题（“ 5至15岁儿童的问题”）
27 。 证明数字的余数 $$$2 ^ {p-1}$ 奇数素数
$$$p$ 等于 $$$1$
（例如： $$$2 ^ {2} = 3a + 1，2 ^ {4} = 5b +1，2 ^ {6} = 7c + 1，2 ^ {10} -1 = 1023 = 10 \ cdot 93）$ 。
《量子》杂志的“连续分数的惊人历险记”中考虑了此问题。

书籍：
“面向5至15岁儿童的任务”，V。I. Arnold。
“微分和积分学的过程” G. M. Fichtenholtz
“数论” A. A. Buchstab
“在数学教科书的页面后面” N. Ya。Vilenkin，L.P。Shibasov，Z.F。Shibasova
“代数” N. Ya。Vilenkin，R。S. Guter，S。I. Schwarzburd
数字算法Ercegovac Milos D.，Lang Tomas
“计算机程序的结构和解释” Harold Abelson，Gerald Sassman

另请参阅
文章 “关于采访中不再提供的一项任务”。
Spice IT Recruitment的博客向各个公司发布了采访任务。
Yandex中的采访任务 。
在此视频中， A。Savvateev通过在特斯拉的采访解决了问题。