引言
许多应用问题导致需要找到非线性方程组的一般解。 找不到非线性方程组的一般解析解。 只有数值方法。
应当指出,一个有趣的事实是,如果我们将所有方程组的形式采用实数形式,则任何方程组都可以用一个等效方程表示
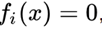
,将它们平方并折叠。
对于数值解,使用了逐次逼近的迭代方法(简单迭代)和各种修改形式的牛顿法。 迭代过程自然可以推广到以下形式的非线性方程组的情况:
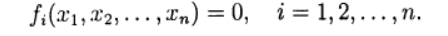
(1)
表示为
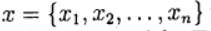
未知向量并定义向量函数
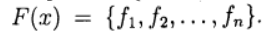
然后以等式的形式写系统(1):
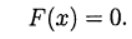
(2)
现在,让我们回到我们心爱的Python,并注意它在想学习的编程语言中的首要地位[1]。
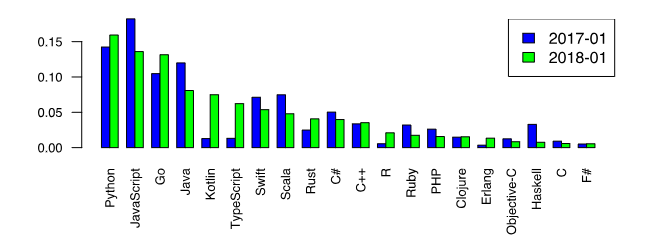
这个事实是考虑在Python中使用数字方法的另一个诱因。 但是,Python爱好者中有一种观点认为,特殊的库函数(例如
scipy.optimize.root,spsolve_trianular,newton_krylov )是通过数值方法解决问题的最佳选择。
仅仅是因为多种多样的模块也将Python推到了顶峰,就很难不同意这一点。 但是,在某些情况下,即使进行了粗略的检查,使用直接已知的方法而不使用SciPy库的特殊功能也会产生良好的结果。 换句话说,新的是被遗忘的旧的。
因此,在出版物[2]中,在计算实验的基础上,证明了用于解决大型非线性方程组的库函数newton_krylov具有比TSLS + WD算法一半的速度。
(两步最小二乘)由NumPy库实现。
本出版物的目的是比较迭代次数,速度以及最重要的是,使用scipy.optimize.root库函数和使用NumPy库实现的牛顿法比较以一百个非线性代数方程组形式求解模型问题的结果。
Scipy.optimize.root求解器功能,用于数值求解代数非线性方程组
选择库函数scipy.optimize.root作为比较基础,因为它具有适用于比较分析的大量方法库。
scipy.optimize.root (
fun,x0,args =(),method ='hybr',jac = None,tol = None,callback = None,ptions = None )
fun-查找根的向量函数。
x0 –求根的初始条件
方法:hybr-使用混合方法的Powell修改;
lm-使用最小二乘法求解非线性方程组。
从文献[3]中可以
看出,方法
broyden1,broyden2和Anderson,线性混合,透溴化,兴奋混合,krylov是牛顿的精确方法。 其余参数是“可选”的,可以在文档中找到。
求解非线性方程组的方法
下面给出的材料确实可以在文献中阅读,例如在[4]中,但是我尊重我的读者,并且为了他的方便起见,如果可能的话,以简化的形式介绍该方法的派生。 那些
不喜欢公式的人可以跳过本节。
在牛顿方法中,
根据线性方程组的解确定了一个新的近似方程组(2)
的解 :
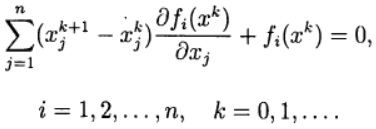
(3)
定义雅可比矩阵:
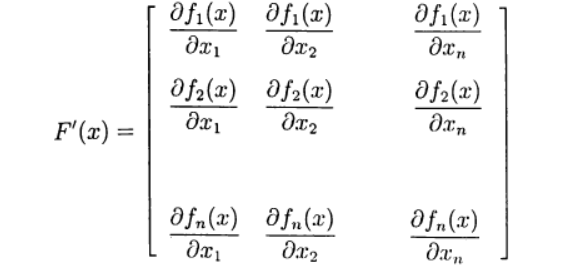
(4)
我们以以下形式写(3):

(5)
类似于(2)的两层迭代方法,用于求解线性代数方程组的许多单步方法可以用以下形式编写:
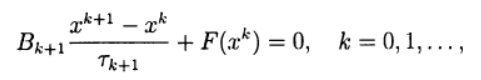
(6)
在哪里
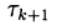
是迭代参数,
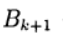
-具有逆的方阵n x n。
使用记录(6)时,牛顿方法(5)对应于以下选择:
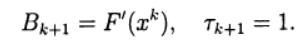
线性方程组(5),用于寻找新的近似值

可以迭代解决。 在这种情况下,我们有一个内部和外部迭代的两阶段迭代过程。 例如,可以根据牛顿法进行外部迭代处理,并且可以基于
赛德尔迭代法进行内部迭代
。在求解非线性方程组时,可以使用标准迭代方法的直接类似物,这些方法用于求解线性方程组。 应用于解决方案(2)的非线性Seidel方法得出:
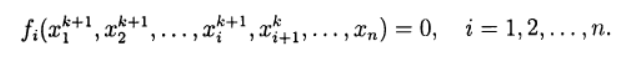
(7)
在这种情况下,可以基于简单迭代法和牛顿法进行各种修改,从非线性方程解中获得新近似值的每个分量。 因此,我们再次回到两阶段迭代方法,其中根据Seidel方法执行外部迭代,并使用Newton方法执行内部迭代。
将牛顿法应用于非线性方程组的近似解的主要计算困难
与需要在每次迭代中求解带有Jacobi矩阵的线性方程组有关 ,并且该矩阵在迭代之间会发生变化。 在改进的牛顿法中,雅可比矩阵仅反转一次:
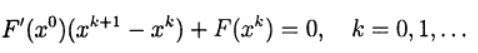
(8)
模型功能选择
这样的选择绝非易事,因为随着变量数量的增加系统中方程式数量的增加,解决方案的结果也不应改变,因为否则无法在比较两种方法时跟踪方程式系统解决方案的正确性。 我为模型功能带来以下解决方案:
n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f
函数f创建了一个由n个非线性方程组成的系统,其解不依赖于方程的数量,并且对于n个变量中的每一个均等于1。一种用于测试模型函数的程序,其结果是使用库函数optimize.root针对不同的求根方法来求解代数非线性方程组的结果
from numpy import* from scipy import optimize import time ti = time.clock() n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f x0 =zeros([n]) sol = optimize.root(f,x0, method='krylov') print('Solution:\n', sol.x) print('Krylov method iteration = ',sol.nit) print('Optimize root time', round(time.clock()-ti,3), 'seconds')
文档[3]中给出的方法中只有一种通过了
对模型函数求解结果的测试,这就是“ krylov”方法 。
n = 100的解:
解决方案:
[1。 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1.]
Krylov方法迭代= 4219
优化根时间7.239秒:
n = 200的解解决方案:
[1.00000018 0.99999972 0.99999985 1.00000001 0.99999992 1.00000049
0.99999998 0.99999992 0.99999991 1.00000001 1.00000013 1.00000002
0.9999997 0.99999987 1.00000005 0.99999978 1.0000002 1.00000012
1.00000023 1.00000017 0.99999979 1.00000012 1.00000026 0.99999987
1.00000014 0.99999979 0.99999988 1.00000046 1.00000064 1.00000007
1.00000049 1.00000005 1.00000032 1.00000031 1.00000028 0.99999992
1.0000003 1.0000001 0.99999971 1.00000023 1.00000039 1.0000003
1.00000013 0.9999999 0.99999993 0.99999996 1.00000008 1.00000016
1.00000034 1.00000004 0.99999993 0.99999987 0.99999969 0.99999985
0.99999981 1.00000051 1.0000004 1.00000035 0.9999998 1.00000065
1.00000061 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.00000059 1.00000056
1.00000047 1.00000016 1.00000018 0.99999988 1.00000061 1.00000002
1.00000033 1.00000034 1.0000004 1.00000046 1.00000009 1.00000024
1.00000017 1.00000014 1.00000054 1.00000006 0.99999964 0.99999968
1.00000005 1.00000049 1.0000005 1.00000028 1.00000029 1.00000027
1.00000027 0.9999998 1.00000005 0.99999974 0.99999978 0.99999988
1.00000015 1.00000007 1.00000005 0.99999973 1.00000006 0.99999995
1.00000021 1.00000031 1.00000058 1.00000023 1.00000023 1.00000044
0.99999985 0.99999948 0.99999977 0.99999991 0.99999974 0.99999978
0.99999983 1.0000002 1.00000016 1.00000008 1.00000013 1.00000007
0.99999989 0.99999959 1.00000029 1.0000003 0.99999972 1.00000003
0.99999967 0.99999977 1.00000017 1.00000005 1.00000029 1.00000034
0.99999997 0.99999989 0.99999945 0.99999985 0.99999994 0.99999972
1.00000029 1.00000016]
Krylov方法迭代= 9178
优化根时间23.397秒
结论:随着方程数量增加两倍,解决方案中出现的错误也很明显。 随着n的进一步增加,解决方案变得不可接受,这可能是由于自动适应步骤而导致的,这是性能急剧下降的相同原因。 但这只是我的猜测。
使用Python 3编写的程序在考虑到关系(1)-(8)的情况下使用改进的牛顿法求模型的功能的程序,该程序使用Python 3编写的程序来求解代数非线性方程组
修正牛顿法求根程序 from numpy import* import time ti = time.clock() def jacobian(f, x): h = 1.0e-4 n = len(x) Jac = zeros([n,n]) f0 = f(x) for i in arange(0,n,1): tt = x[i] x[i] = tt + h f1= f(x) x[i] = tt Jac [:,i] = (f1 - f0)/h return Jac, f0 def newton(f, x, tol=1.0e-9): iterMax = 50 for i in range(iterMax): Jac, fO = jacobian(f, x) if sqrt(dot(fO, fO) / len(x)) < tol: return x, i dx = linalg.solve(Jac, fO) x = x - dx print ("Too many iterations for the Newton method") n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f x0 =zeros([n]) x, iter = newton(f, x0) print ('Solution:\n', x) print ('Newton iteration = ', iter) print('Newton method time', round(time.clock()-ti,3), 'seconds')
n = 100的解:
解决方案:
[1。 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1.]
牛顿迭代= 13
牛顿法时间0.496秒
n = 200的解:
解决方案:
[1。 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
牛顿迭代= 14
牛顿法时间1.869秒
为了确保程序确实能解决系统问题,我们重写了避免返回值为1的根的模型函数:
n=10 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i]*sin([i]) - x[i-1] - 2*x[i+1] - 2+e**-x[i] f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f
我们得到:
解决方案:
[0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
牛顿迭代= 16
牛顿法时间0.046秒
结论:
当模型功能更改时,该程序也可以运行。现在,我们返回初始模型函数,并检查n的更大范围,例如2和500。
n = 2
解决方案:
[1。 1.]
牛顿迭代= 6
牛顿法时间0.048秒
n = 500
n = 500解决方案:
[1。 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1。
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
牛顿迭代= 15
牛顿法时间11.754秒
结论:
当使用给定的模型函数求解非线性方程组时,使用改进的牛顿方法用Python编写的程序比使用库函数的库函数optimize.root(f,x0,method ='krylov')求解时,其解决方案具有更高的稳定性。 关于最终结论的速度,由于步骤控制的方法不同,因此无法得出结论。
参考文献:
- 编程语言评级2018。
- Cooper I.V.,法利奇克(Faleychik B.V. 大型均方方程组的具有均方根误差抑制的非矩阵迭代过程。
- scipy.optimize.root。
- 瓦比雪切维奇 数值方法:计算车间。 -M.:“LIBROCOM”书屋,2010年。-320页。