使用Python建立天体的轨道

确定轨道的参考系统

为了找到经典力学中的相对运动轨迹，使用所有参考系（惯性和非惯性）中绝对时间的假设。

使用此假设，我们考虑两个不同参考系中同一点的运动 $$$K$ 和 $$$K ^ {'}$ 其中第二个相对于第一个以任意速度移动 $$$\ vec {V（t）} = \点{\ vec {R（t）}}$ 在哪里 $$$\ vec {R（t）}$ 半径向量，描述坐标系原点的位置 $$$K ^ {'}$ 相对于参照系 $$$K$ ）

我们将描述系统中一点的运动 $$$K ^ {'}$ 半径向量 $$$\ vec {r ^ {'}}（t）$ 从系统原点定向 $$$K ^ {'}$ 到该点的当前位置。 然后考虑中的点相对于参考系的运动 $$$K$ 用半径矢量描述 $$$\ vec {r（t）}$ ：

$$$\ vec {r}（t）= \ vec {r ^ {'}}（t）+ \ vec {R}（t）$ ，（1）

和相对速度 $$$\ vec {v（t）}$

$$$\ vec {v}（t）= \点{\ vec {r ^ {'}}}（t）+ \点{\ vec {R}}（t）$ ，（2）

在哪里 $$$\点{\ vec {r ^ {'}}}（t）$ -点相对于系统的速度 $$$K ^ {'}$ ; $$$\点{\ vec {R}}（t）$ 帧速度 $$$K ^ {'}$ 相对于参照系 $$$K$ 。



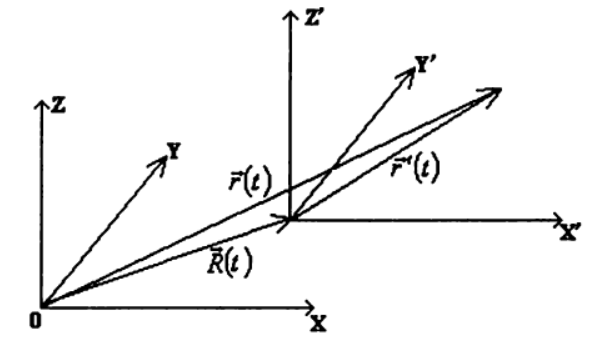
因此，找到任意参考系中点的运动定律 $$$K$ 必要的：

1）设定运动定律的要点- $$$\ vec {r ^ {'}}（t）$ 相对于参照系 $$$K ^ {'}$ ;
2）设定运动定律- $$$\ vec {R}（t）$ 参考系统 $$$K ^ {'}$ 相对于参照系 $$$K$
3）确定点的运动定律- $$$\ vec {r}（t）= \ vec {r ^ {'}}（t）+ \ vec {R}（t）$ 相对于参照系 $$$K$ 。

在日心参考系中构造月球轨道

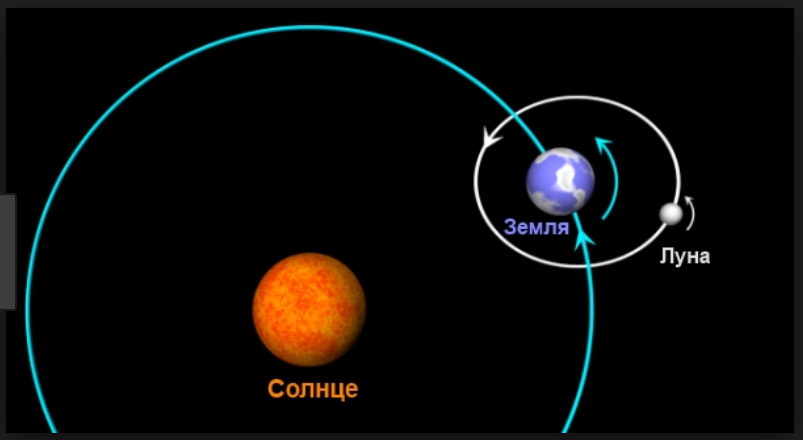
在日心参考系统（系统 $$$K$ ）地球绕半径移动
$$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ km（流通周期 $$$T_ {1} = 3,156 \ cdot 10 ^ {7}$ s。）。 月亮又绕半径（圆）绕地球（系统K'）运动 $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ 公里 （流通期 $$$T_ {2} = 2.36 \ cdot 10 ^ {6}$ s 众所周知[1,2]，当实体点沿半径的圆移动时 $$$R$ 角速度恒定 $$$\ omega$ 从原点到点的当前位置绘制的半径向量的坐标会根据以下规律变化：

$$

$$\ vec {R（t）} = \ binom {R \ cdot cos（\ omega \ cdot t + \ varphi _ {0}）} {R \ cdot sin（\ omega \ cdot t + \ varphi _ {0}）} = \ binom {R \ cdot cos（\ frac {2 \ pi} {T}）+ \ varphi _ {0}）} {R \ cdot sin（\ frac {2 \ pi} {T} + \ varphi _ { 0}）}，（3）$$

在哪里 $$$\ varphi _ {0}$ -表征粒子在时间的位置的初始阶段 $$$t = 0$ ，将来我们将假定它等于零。 替换为（3） $$$R$ 在 $$$R_ {1}$ 和 $$$R_ {2}$ 并代入（1），我们得到日心轴坐标系中月亮半径向量对时间的依赖关系：

$$

$$\ vec {r（t）} = \ binom {x（t）} {y（t）} = \ binom {R_ {2} cos（\ frac {2 \ pi} {T_ {2}} t）+ R_ {1} cos（\ frac {2 \ pi} {T_ {1}} t）} {R_ {2} sin（\ frac {2 \ pi} {T_ {2}} t）+ R_ {1} sin （\ frac {2 \ pi} {T_ {1}} t）}，（4）$$

表达式（4）设置月球的轨道（ $$$y = y（x（t））$ ）以参数形式显示，其中参数为时间。 为了使用Python建立所需的轨道，我们设置了轨道的半径以及地球和月球的自转周期。

地球以日心坐标系（ $$$K$ ）其轨道半径和公转周期分别相等 $$$R_ {1} = 1.496 \ cdot 10 ^ {8} km，T_ {1} = 3.156 \ cdot 10 ^ {7} s$ 月亮在坐标系中绕地球运动（ $$$K ^ {'}$ ）其轨道半径和公转周期分别相等 $$$R_ {2} = 3.844 \ cdot 10 ^ {5}公里，T_ {2} = 2.36 \ cdot 10 ^ {6} s$ 。

鉴于（4），我们确定坐标与时间的依存关系的函数：

$$

$$\ binom {（X（t）= R_ {1} \ cdot cos（\ frac {2 \ pi} {T_ {1}} \ cdot t），Y（t）= R_ {1} \ cdot sin（\ frac {2 \ pi} {T_ {1}} \ cdot t）} {x（t）= R_ {2} \ cdot cos（\ frac {2 \ pi} {T_ {2}} \ cdot t），y （t）= R_ {2} \ cdot sin（\ frac {2 \ pi} {T_ {2}} \ cdot t）}，（5）$$

使用（5），我们获得月球轨道的一对坐标：

$$

$$\ binom {X_ {g}（t）= X（t）+ x（t）} {Y_ {g}（t）= Y（t）+ y（t）}，（6）$$

我们设置坐标N = 1000的点数和地球自转间隔的离散时间 $$$dt = \ frac {T_ {1}} {N}$ 。 我们将编写一个程序并为正坐标更改区域构建图形：


我们得到：


图1

创建的时间表可让您扩展训练任务，并查看如果月球轨道半径为，月球轨道将是什么 $$$R_ {2} = 3.844 \ cdot 10 ^ {7}$ 。 。 甚至对天文学没有专门知识的读者都清楚，月球在地球的非引力场中不可能有这样的轨道，并且使用假想半径来研究环的出现条件 。 我们将对该程序进行适当的更改：


我们得到：


图2

比较图2所示的月球轨道。 1和2，我们发现它们之间的显着差异。 为了解释这些差异的原因，有必要比较月球在第一和第二种情况下的线速度与地球的线速度。

由于地球相对于太阳的线速度的方向以及月球相对于地球的线速度的方向随时间变化，因此速度在大小上保持恒定。

作为在日心坐标系中月球与地球的线速度之比的定量特征，应该选择地球的线速度模块与月球的线速度在地球的线速度方向上的投影之间的差：

$$

$$v_ {o}（t）= \左| \ vec {V}（t）\右|-\ frac {（\ vec {V}（t）\ cdot \ vec {v}（t））} {\左| \ vec {V}（t）\ right |}，（7）$$

我们定义了描述地球和月球速度分量变化规律的函数：

$$

$$\开始{矩阵} V_ {x}（t）= \ frac {d} {dt} X（t），V_ {y}（t）= \ frac {d} {dt} Y（t）＆\\ vx（t）= \ frac {d} {dt} x（t），vy（t）= \ frac {d} {dt} y（t）\ end {matrix}，（8）$$

为了确定最终速度，并考虑了投影，我们使用以下关系式：

$$$D（t）= \ sqrt {V_ {x}（t）^ {2} + V_ {y}（t）^ {2}}-\ sqrt {vx（t）^ {2} + vy（t） ^ {2}} \ cdot \ frac {V_ {x}（t）\ cdot vx（t）+ V_ {y}（t）\ cdot vy（t）} {\ sqrt {V_ {x}（t）^ {2} + V_ {y}（t）^ {2}} \ cdot \ sqrt {vx（t）^ {2} + vy（t）^ {2}}}，（9）$

我们将在考虑到（5），（8），（9）和月球轨道半径的情况下编写程序 $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ 公里。：


我们得到：


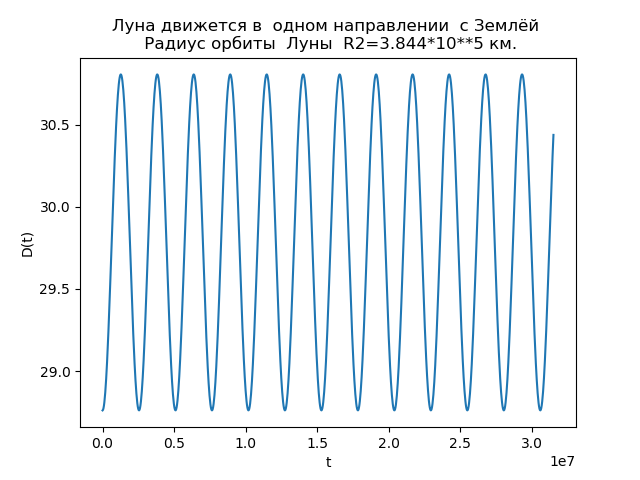图3。

我们将编写一个程序，考虑到（5），（8），（9）以及月球轨道半径R2 = 3.844 * 10 ** 7 km：


我们得到：


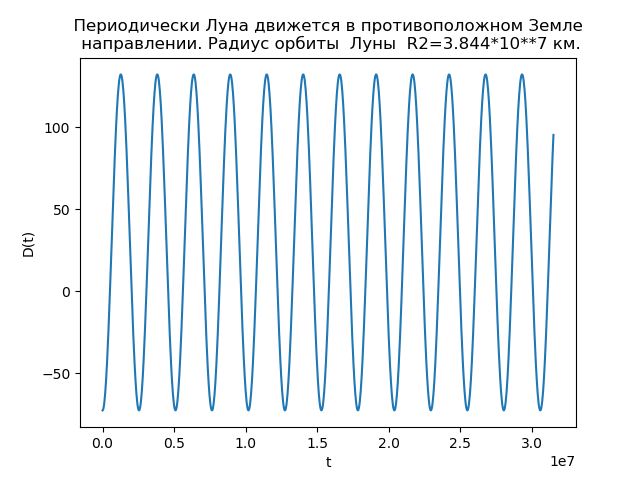图4。

对相关性的分析使我们能够解释轨道不同的原因。 的函数D（t） $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ km始终是正的，也就是说，月亮始终沿地球运动的方向移动，并且不形成环。 在 $$$R_ {2} = 3.844 \ cdot 10 ^ {7}$ 公里值 $$$D（吨）$ 取负值，并且有时月亮在与地球运动方向相反的方向上运动，因此轨道具有回圈。 这就是在计算中使用月球不存在的含义。

在与地球有关的参考系中构造火星轨道

。


在日心参考系统（系统K）中，地球在半径为圆的范围内运动 $$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ km，循环周期 $$$T_ {1} = $ 365.2$ 一天，火星沿着椭圆的半长轴移动 $$$am = 2.28 \ cdot 10 ^ {8}$ 公里，火星的革命时期 $$$T_ {m} = $ 689.9$ 天。，轨道的离心率 $$$e = $ 0.09$ [3]。 地球运动由表达式（3）定义的半径矢量R（t）描述。 由于火星的轨道是椭圆形，因此 $$$x = x（t），y = y（t）$ 从时间开始参数设置[4]：

$$$x（\ varepsilon）= a_ {m} \ cdot（cos（\ varepsilon）-e）$ ，（10）

$$$y（\ varepsilon）= a_ {m} \ cdot \ sqrt {1-e ^ {2}} \ cdot sin（\ varepsilon）$ ，（11）

$$$t（\ varepsilon）= \ frac {T_ {m}} {2 \ pi} \ cdot（\ varepsilon-e \ cdot sin（\ varepsilon））$ ，（12）

完整的椭圆旋转对应于参数<img的更改 $$$\ varepsilon$ 从0到 $$$2 \ pi$ 。 为了建立火星的轨道，有必要在描述地球和火星在日心参考系中的位置的同时，计算半径矢量的坐标，然后根据 $$$\ vec {r ^ {'}}（t）= \ vec {r}（t）-\ vec {R}（t）$ 计算与地球相关的参考系中火星的坐标。

为了在与地球连接的参考系中建立火星的轨道，我们使用先前给定的地球和火星轨道参数，关系（10）-（12），以及地球坐标的关系：

$$$X（t）= R_ {1} \ cdot cos（\ frac {2 \ pi} {T_ {1}} t）$ ，（13）

$$$Y（t）= R_ {1} \ cdot sin（\ frac {2 \ pi} {T_ {1}} t）$ ，（14）

应当指出，火星绕太阳公转的周期为 $$$K = 9$ ，则应根据以下关系确定进行计算的点数及其之间的距离：

$$$N = 4000 \ cdot K，\ varepsilon_ {i} = \ frac {2 \ pi} {N} \ cdot i，i = 0 ... N$ （15）


我们得到：


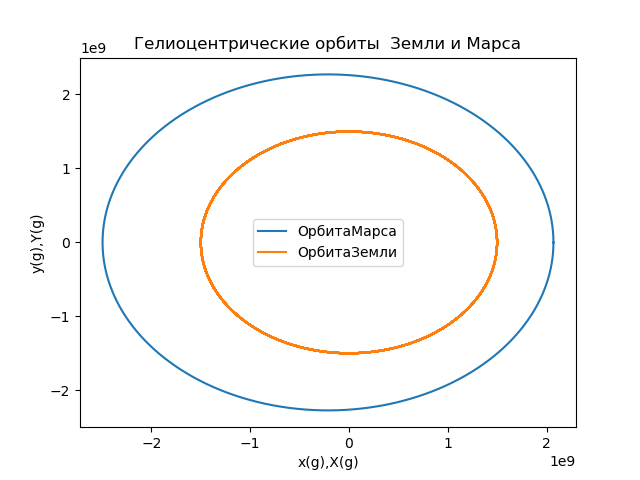图5

我们计算半径向量的坐标，以描述火星在与地球连接的参考系中的位置，并使用以下关系式构建轨道（图6）：

$$$x1_ {i} = x（\ varepsilon_ {i}）-X（t（\ varepsilon_ {i}）），y1_ {i} = y（\ varepsilon_ {i}）-Y（t（\ varepsilon_ {i} ））$ （16）


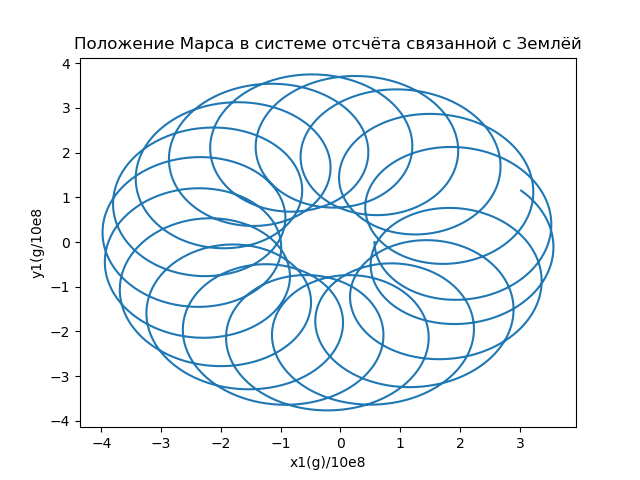图6

火星运动的另一个重要特征（主要用于行星际太空飞行）是地球与火星之间的距离（t），它是由描述火星在与地球相关的参考系中的位置的半径向量的模数确定的。 图7显示了地球与火星之间的距离与以地球年计的时间的关系。


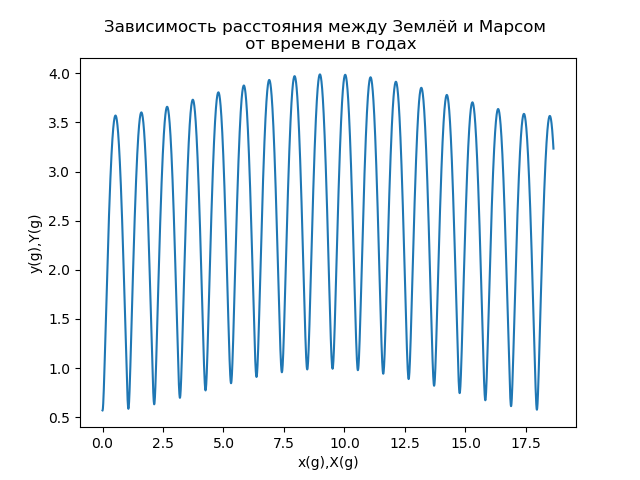图7

对图7所示依赖性的分析表明，地球与火星之间的距离是时间的复杂周期函数。 如果我们使用信号理论[5]的术语，那么我们可以说依赖关系s（t）是幅度调制信号，通常表示为定义幅度调制（包络）的高频（载波）和低频函数这两个函数的乘积：

$$$u（t）=（\ bar {u} + a \ cdot sin（\ omega_ {1} t））\ cdot（1+ \ Delta a \ cdot sin（\ omega_ {2} t））$ （17）

在哪里 $$$\ bar {u}$ -函数的常数 $$$（吨）$ ; $$$一$ -信号幅度； $$$\ omega_ {1}$ -载波频率； $$$\三角洲$ -设置幅度调制深度的函数的幅度； $$$\ omega_ {2}$ -调制功能的频率。

从图7中可以看出，载波的周期约为2年，调制功能的周期约为17年[6]。

哈雷彗星日心轨道的构造

1986年2月9日，哈雷彗星最后一次穿过近日点（离太阳最近的轨道点）。 （太阳本身被认为位于原点。）

哈雷彗星当时的坐标和速度分量相等 $$$p_ {0} =（0.325514，0.459460，0.166229）$ 和 $$$v_ {0} =（–9.096111，–6.916686，–1.305721）$ 分别以长度的天文单位-a.u.d.或简称a.u.表示距离。 （天文单位，即地球轨道的主要主要半轴的长度）和时间（以年为单位）。 在这些度量单位中，彗星的三维运动方程具有以下形式：

$$

$$\ left \ {\ begin {matrix} \ frac {d ^ {2} x} {dt ^ {2}} =-\ frac {\ mu \ cdot x} {r ^ {3}} \\ \ frac { d ^ {2} y} {dt ^ {2}} =-\ frac {\ mu \ cdot y} {r ^ {3}} \\ \ frac {d ^ {2} z} {dt ^ {2} } =-\ frac {\ mu \ cdot z} {r ^ {3}} \ end {matrix} \ right。，（18）$$

（18）

其中： $$$\ mu = 4 \ pi ^ {2}，r = \ sqrt {x ^ {2} + y ^ {2} + z ^ {2}}$


我们得到：









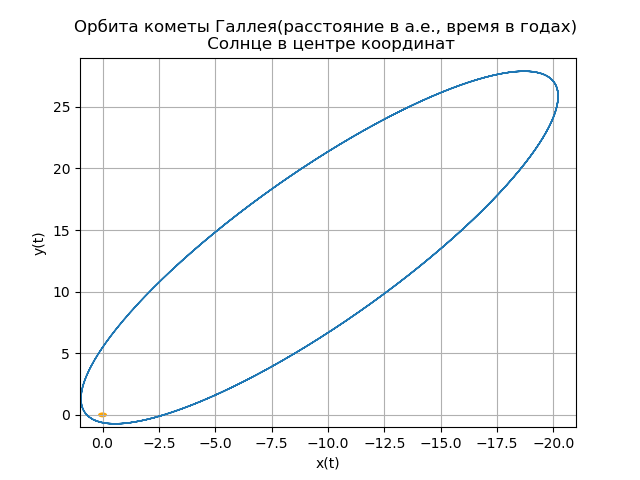
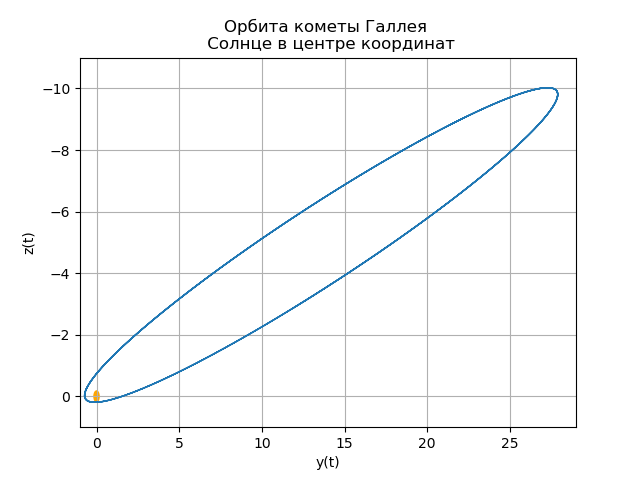
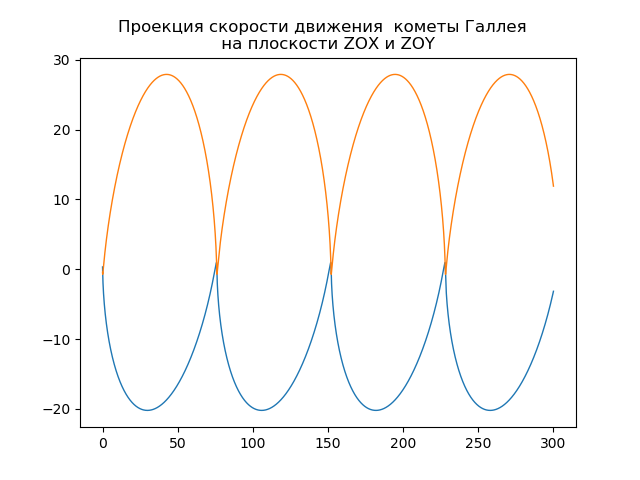你自己的彗星

尝试一个实验。 晚上，您将望远镜安装在离家不远的小山顶上。 夜晚应该晴朗，万里无云，繁星密布，如果幸运的话向您微笑：在凌晨0.30时，您会注意到一颗新的彗星。

经过第二天晚上的反复观察，您将能够在第一天晚上计算其坐标。 日心轴坐标系中的坐标：P0 =（x0，y0，z0），速度矢量v0 =（vx0，vy0，vz0）。

使用此数据，确定：

• 彗星到太阳的距离在近日点（最靠近太阳的轨道点）和顶峰（距离太阳最远的轨道点）处；
• 穿过近日点和顶点时的彗星速度；
• 彗星绕太阳公转的时期；
• 接下来的两个日期，彗星穿过近日点。

如果我们以天文单位测量距离，并以年为单位测量时间，那么彗星的运动方程将采用（18）的形式。 对于您自己的彗星，选择与哈雷彗星相同顺序的任意起始坐标和速度。

如有必要，请重新选择初始位置和速度矢量，直到获得超出地球轨道的似真的偏心轨道为止（就像大多数真实的彗星一样）。

参考文献：

1. Feynman R.，Leighton R.，Sands M. Feynman物理讲座。 第三版。 T.-1.-2。 M .：米尔，1977年。
2. Matveev A.N.力学和相对论。 M .：更高。 学校，1986年。
3. 物理百科全书。 T. 3. M .：《大俄罗斯百科全书》，1992年。
4. Landau L.D.，Lifshits E.M.理论物理课程。 力学。 M .:富马吉兹（Fu-matgiz），1958年。
5. Baskakov S.I.无线电工程电路和信号。 M .：更高。 1988年。
6. 波什涅夫 使用mathcad软件包对物理过程进行计算机模拟。