通常,使用数值矩阵并特别是线性代数方程组求解是一个经典的数学和算法问题,已广泛用于建模和计算大量业务流程(例如,计算成本时)。 在创建和操作1C:企业配置时,许多开发人员面临着手动实施SLAU计算算法的需求,然后面临着等待解决方案的漫长问题。
“ 1C:企业” 8.3.14将包含一些功能,这些功能可以通过使用基于图论的算法来显着减少求解线性方程组的时间。
它经过优化,可用于结构稀疏的数据(即方程中包含不超过10%的非零系数),并且在平均水平和最佳情况下,可证明渐近(n⋅log(n)⋅log(n)),其中n为变量的数量,在最坏的情况下(系统充满〜100%时),其渐近行为可与经典算法(Θ(n
3 ))相提并论。 同时,在具有约10
5个未知数的系统上,该算法显示的加速度比专用线性代数库(例如
superlu或
lapack )中实现的加速度高数百倍。
 重要提示:本文和所描述的算法要求在大学一年级时了解线性代数和图论。
重要提示:本文和所描述的算法要求在大学一年级时了解线性代数和图论。以图表形式显示SLAE
考虑最简单的线性方程组稀疏系统:
 注意:系统是随机生成的,稍后将用于演示算法的步骤
注意:系统是随机生成的,稍后将用于演示算法的步骤乍一看,便出现了与另一个数学对象的关联-图邻接矩阵。 那么,为什么不将数据转换为邻接表,在运行时节省RAM并加快对非零系数的访问呢?
为此,只需对矩阵进行转置并建立不变量
“ A [i] [j] = z⇔第i个变量以系数z进入第j个方程” ,然后对于任何非零A [i] [j]构造相应的边从顶点i到顶点j。
结果图将如下所示:
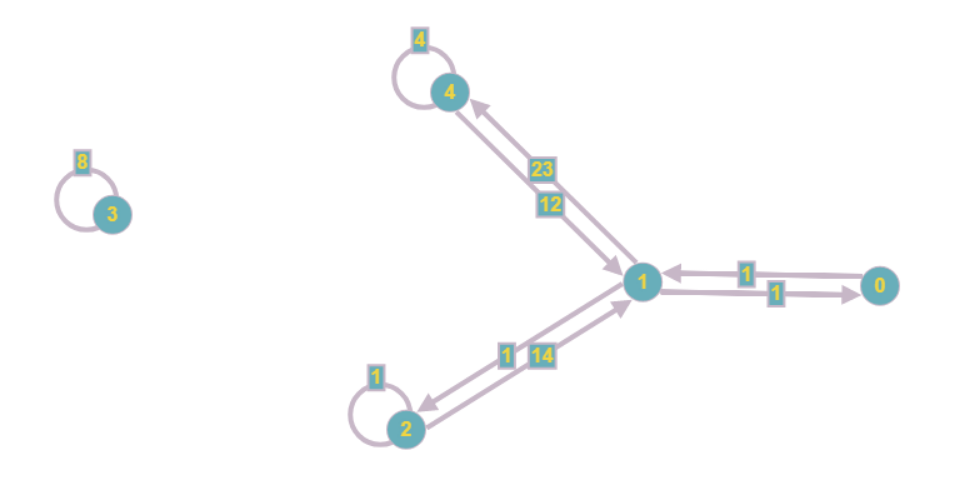
即使在视觉上,它也变得不那么麻烦,并且渐近存储成本从O(n
2 )减少到O(n + m),其中m是系统中系数的数量。
隔离弱连接的组件
考虑结果实体时想到的第二个算法思想是:“分而治之”的原理的使用。 在图形方面,这导致将一组顶点分离为弱连接的组件。
让我提醒您,弱连接的分量是这样一个顶点的子集,其中最大的一个是在任意两个顶点之间存在从无向图中的边开始的路径。 我们可以从原始图中获得无向图,例如,通过在每个边上添加相反的图(随后删除)。 然后,连接的一个顶点将包含我们深入图时可以到达的所有顶点。
分离弱连接的组件后,该图将采用以下形式:
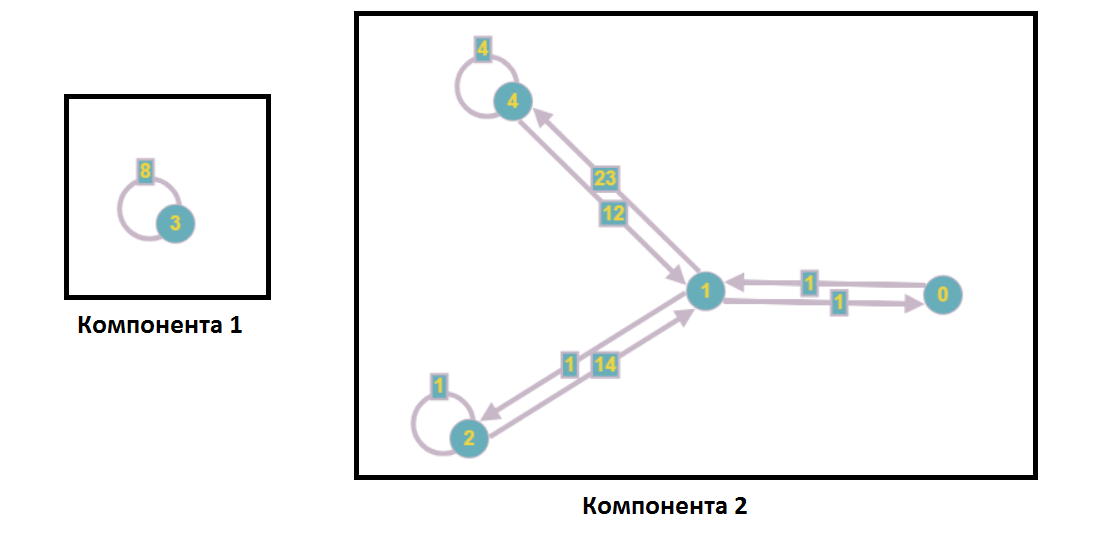
作为线性方程组分析的一部分,这意味着方程中不包含第一个组件的顶点以及第二个组件的数量,反之亦然,也就是说,我们可以独立(例如并行)求解这些子系统。
图顶点减少
该算法的下一步就是针对稀疏矩阵的优化。 即使在示例中的图表中,也存在“悬空”峰,这意味着某些方程式仅包含一个未知数,并且,正如我们所知,该未知数的值很容易找到。
为了确定这样的方程式,建议存储列表的阵列,该列表包含方程式中包括的具有该数组元素的数量的变量的数量。 然后,当列表达到单位大小时,我们可以缩小非常“唯一”的顶点,并在该顶点进入的其他方程式中告知其余方程式。
因此,我们可以在完全处理组件之后立即从示例中减少顶点3:
8⋅3=4⇒3=1/2
由于方程式0仅包含一个变量,因此我们类似地对其进行处理:
1⋅x1=1⇒x1=1
找到此结果后,其他方程式也会更改:
$$显示$$1⋅_1+1⋅_2=3⇒1⋅_2= 3-1 = 2 $$显示$$
该图采用以下形式:
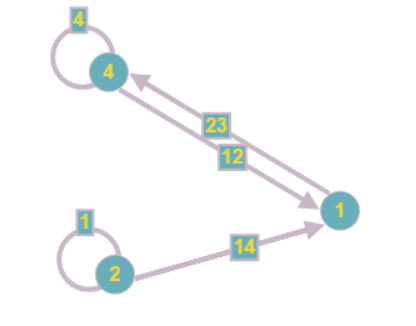
请注意,缩小一个顶点时,可能还会出现其他顶点,其中也包含一个未知顶点。 因此,应重复执行该算法步骤,直到可以减少至少一个顶点为止。
图重建
最细心的读者可能会注意到,图形中的每个顶点的发生程度至少为两个,并且不可能继续持续减小顶点的情况是可能的。
此类图的最简单示例:每个顶点的出现度等于2,所有顶点均无法缩小。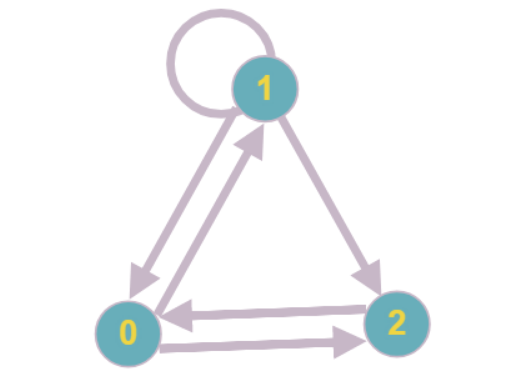
作为稀疏矩阵优化的一部分,假定此类子图的大小较小,但是,您仍然必须使用它们。 为了计算作为方程子系统的一部分的未知数的值,建议使用经典方法求解SLAE(这就是为什么引言指出,对于方程中所有或几乎所有系数都不为零的矩阵,我们的算法将具有与标准方程相同的渐进复杂度)
例如,您可以将还原后剩余的顶点集重新带回矩阵形式,并对其应用
高斯方法来求解SLAE 。 因此,我们将获得精确的解决方案,并且由于处理的不是整个系统,而是仅处理了一部分系统,因此算法的速度将降低。
算法测试
为了测试该算法的软件实现,我们采用了多个大体积方程组的真实系统以及大量随机生成的系统。
随机方程组的生成是通过在两个随机顶点之间依次添加任意权重的边来实现的。 总体而言,系统已满5-10%。 通过将获得的答案代入原始方程组,可以验证解的正确性。
 系统范围从1,000到200,000个未知数
系统范围从1,000到200,000个未知数为了比较性能,我们使用了最受欢迎的库来解决线性代数问题,例如superlu和lapack。 当然,这些库专注于解决各种各样的问题,并且SLAE的解决方案没有以任何方式进行优化,因此速度差异非常明显。
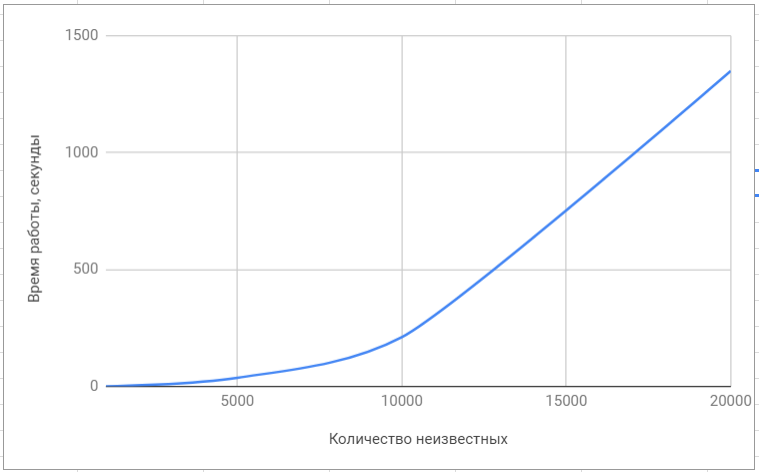 测试lapack库
测试lapack库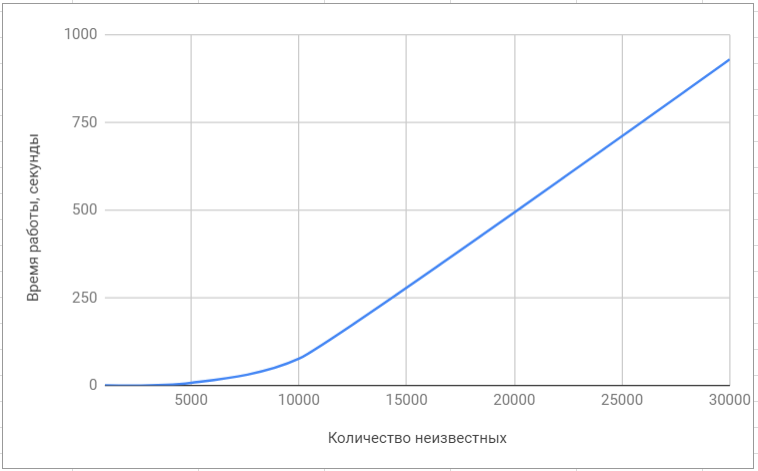 测试库“ superlu”
测试库“ superlu”这是我们的算法与流行库中实现的算法的最终比较:

结论
即使您不是1C:企业配置开发人员,也可以在实现SLAE求解算法时使用本文中介绍的思想和优化方法,也可以在与矩阵相关的一类线性代数问题上使用本文描述的思想和优化方法。
对于1C开发人员,我们补充说SLAE解决方案的新功能支持并行使用计算资源,并且您可以调整使用的计算线程数。