🐨 👋 📏 概率比特币挖掘方法 💫 🖕🏽 👩🏿‍🤝‍👩🏽

我认为周二有点废话不会伤害工作周。我有一个爱好，在业余时间我试图弄清楚如何破解比特币挖掘算法，避免愚蠢的鼻子搜索，并找到一种以最小的能耗解决哈希匹配问题的解决方案。我必须立即说出结果，当然，我还没有实现，但是，为什么不写出脑中产生的想法呢？他们需要放在某个地方...

尽管存在以下想法的妄想，但我认为本文对正在学习的人可能有用

C ++语言及其模板
一些数字电路
一点概率论和概率算法
比特币哈希算法详细

我们从哪里开始？

也许是这个列表中最后一个最无聊的项目？耐心，那么会更有趣。
让我们详细考虑用于计算比特币哈希函数的算法。它是简单的F（x）= sha256（sha256（x）），其中x是输入的80个字节，块头以及块的版本号，上一个块哈希，merkle根，时间戳，位和随机数。这是传递给哈希函数的最新块头的示例：

//blk=533522 0x00,0x00,0x00,0x20, 0x6d,0xa5,0xdd,0xb5,0x78,0x04,0x08,0x80,0xae,0x3d,0xed,0xc5,0x8e,0xe9,0x74,0x93,0x93,0x6d,0x6a,0xf4,0x0e,0x80,0x30,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0xdf,0x3e,0xb0,0xf4,0x92,0xbf,0xe9,0xb8,0xc8,0x12,0x1f,0x84,0xdd,0x35,0xe1,0x38,0x09,0xcc,0x28,0xc2,0x33,0x53,0x90,0x4e,0x15,0x49,0x5e,0xc7,0xb0,0x78,0x35,0x91, 0x82,0xDB,0x57,0x5B, 0x17,0x5A,0x36,0x17, 0xAA,0x02,0x44,0x22, //blk=533523 0x00,0x00,0x00,0x20, 0x6a,0x27,0x37,0xc3,0x1f,0x68,0xf8,0xe3,0x03,0xa3,0x5d,0xff,0x2d,0x97,0x39,0xaf,0x81,0xa2,0xf5,0xf0,0x7c,0xdb,0x34,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0xa1,0xb8,0x4f,0x75,0x66,0xf3,0xf3,0x8e,0x78,0xf7,0xa2,0xa2,0xa2,0x19,0xa1,0x18,0x45,0xfa,0x58,0x53,0xe4,0x05,0x50,0x12,0x57,0xa1,0xab,0x2c,0x39,0xe6,0x1f,0x63, 0xA0,0xDB,0x57,0x5B, 0x17,0x5A,0x36,0x17, 0x84,0x7B,0x86,0xE7, //blk=533524 0x00,0x00,0x00,0x20, 0xb3,0xc7,0xaa,0x07,0x26,0xdb,0xe8,0x58,0x19,0xa8,0xb9,0x53,0x08,0x62,0x8b,0xca,0x58,0x00,0x69,0x64,0x58,0x69,0x1a,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x4e,0xfc,0xf4,0x5c,0xad,0x31,0x44,0x5b,0xb1,0x13,0x80,0x03,0xe0,0xfd,0x04,0x24,0x86,0xcc,0x7a,0x8c,0xa7,0x7c,0x30,0x60,0x05,0x6f,0x43,0xcf,0x25,0x45,0x8f,0xd8, 0x80,0xDE,0x57,0x5B, 0x17,0x5A,0x36,0x17, 0xF7,0x2B,0x3B,0x42,

这组字节是非常有价值的材料，因为对于矿工而言，通常不容易确定形成报头时字节应遵循的顺序，通常会颠倒低字节和高字节的位置（字节序）。

因此，从块头开始，将80个字节视为sha256哈希，然后从结果中考虑另一个sha256。
如果您查看不同的资料，sha256算法本身通常包含四个功能：

无效的sha256_init（SHA256_CTX * ctx）;
void sha256_transform（SHA256_CTX * ctx，常量字节数据[]）；
void sha256_update（SHA256_CTX * ctx，常量字节数据[]，size_t len）;
void sha256_final（SHA256_CTX * ctx，BYTE hash []）;

计算散列时调用的第一个函数是sha256_init（），它将恢复SHA256_CTX结构。除了八个32位状态字（最初用特殊字填充）外，没有什么特别的：

 void sha256_init(SHA256_CTX *ctx) { ctx->datalen = 0; ctx->bitlen = 0; ctx->state[0] = 0x6a09e667; ctx->state[1] = 0xbb67ae85; ctx->state[2] = 0x3c6ef372; ctx->state[3] = 0xa54ff53a; ctx->state[4] = 0x510e527f; ctx->state[5] = 0x9b05688c; ctx->state[6] = 0x1f83d9ab; ctx->state[7] = 0x5be0cd19; }

假设我们有一个需要计算其哈希值的文件。我们读取具有任意大小的块的文件，并调用sha256_update（）函数，将指针传递给块数据和块长度。该函数在状态数组中的SHA256_CTX结构中累积哈希：

 void sha256_update(SHA256_CTX *ctx, const BYTE data[], size_t len) { uint32_t i; for (i = 0; i < len; ++i) { ctx->data[ctx->datalen] = data[i]; ctx->datalen++; if (ctx->datalen == 64) { sha256_transform(ctx, ctx->data); ctx->bitlen += 512; ctx->datalen = 0; } } }

sha256_update（）本身会调用主函数sha256_transform（），该函数已经接受固定长度为64字节的块：

 /****************************** MACROS ******************************/ #define ROTLEFT(a,b) (((a) << (b)) | ((a) >> (32-(b)))) #define ROTRIGHT(a,b) (((a) >> (b)) | ((a) << (32-(b)))) #define CH(x,y,z) (((x) & (y)) ^ (~(x) & (z))) #define MAJ(x,y,z) (((x) & (y)) ^ ((x) & (z)) ^ ((y) & (z))) #define EP0(x) (ROTRIGHT(x,2) ^ ROTRIGHT(x,13) ^ ROTRIGHT(x,22)) #define EP1(x) (ROTRIGHT(x,6) ^ ROTRIGHT(x,11) ^ ROTRIGHT(x,25)) #define SIG0(x) (ROTRIGHT(x,7) ^ ROTRIGHT(x,18) ^ ((x) >> 3)) #define SIG1(x) (ROTRIGHT(x,17) ^ ROTRIGHT(x,19) ^ ((x) >> 10)) /**************************** VARIABLES *****************************/ static const uint32_t k[64] = { 0x428a2f98,0x71374491,0xb5c0fbcf,0xe9b5dba5,0x3956c25b,0x59f111f1,0x923f82a4,0xab1c5ed5, 0xd807aa98,0x12835b01,0x243185be,0x550c7dc3,0x72be5d74,0x80deb1fe,0x9bdc06a7,0xc19bf174, 0xe49b69c1,0xefbe4786,0x0fc19dc6,0x240ca1cc,0x2de92c6f,0x4a7484aa,0x5cb0a9dc,0x76f988da, 0x983e5152,0xa831c66d,0xb00327c8,0xbf597fc7,0xc6e00bf3,0xd5a79147,0x06ca6351,0x14292967, 0x27b70a85,0x2e1b2138,0x4d2c6dfc,0x53380d13,0x650a7354,0x766a0abb,0x81c2c92e,0x92722c85, 0xa2bfe8a1,0xa81a664b,0xc24b8b70,0xc76c51a3,0xd192e819,0xd6990624,0xf40e3585,0x106aa070, 0x19a4c116,0x1e376c08,0x2748774c,0x34b0bcb5,0x391c0cb3,0x4ed8aa4a,0x5b9cca4f,0x682e6ff3, 0x748f82ee,0x78a5636f,0x84c87814,0x8cc70208,0x90befffa,0xa4506ceb,0xbef9a3f7,0xc67178f2 }; /*********************** FUNCTION DEFINITIONS ***********************/ void sha256_transform(SHA256_CTX *ctx, const BYTE data[]) { uint32_t a, b, c, d, e, f, g, h, i, j, t1, t2, m[64]; for (i = 0, j = 0; i < 16; ++i, j += 4) m[i] = (data[j] << 24) | (data[j + 1] << 16) | (data[j + 2] << 8) | (data[j + 3]); for (; i < 64; ++i) m[i] = SIG1(m[i - 2]) + m[i - 7] + SIG0(m[i - 15]) + m[i - 16]; a = ctx->state[0]; b = ctx->state[1]; c = ctx->state[2]; d = ctx->state[3]; e = ctx->state[4]; f = ctx->state[5]; g = ctx->state[6]; h = ctx->state[7]; for (i = 0; i < 64; ++i) { t1 = h + EP1(e) + CH(e, f, g) + k[i] + m[i]; t2 = EP0(a) + MAJ(a, b, c); h = g; g = f; f = e; e = d + t1; d = c; c = b; b = a; a = t1 + t2; } ctx->state[0] += a; ctx->state[1] += b; ctx->state[2] += c; ctx->state[3] += d; ctx->state[4] += e; ctx->state[5] += f; ctx->state[6] += g; ctx->state[7] += h; }

读取完整个哈希文件并将其传输到sha256_update（）函数后，剩下的就是调用最后的sha256_final（）函数，如果文件大小不是64字节的倍数，它将添加其他填充字节，在最后一个数据块的末尾写入总数据长度，然后将执行最后的sha256_transform（）。
哈希结果保留在状态数组中。

可以这么说，这是“高层次”。

当然，相对于比特币矿工，开发人员正在考虑如何考虑更小，更高效。

很简单：标头仅包含80个字节，而不是64个字节的倍数。因此，有必要使第一个sha256已经执行两个sha256_transform（）。但是，幸运的是，对于矿工而言，该块的现时值位于标头的末尾，因此第一个sha256_transform（）只能执行一次-这就是所谓的中间状态。接下来，矿工遍历所有nonse选项，它们是40亿，2 ^ 32，并将它们替换为第二sha256_transform（）的相应字段。此转换完成了第一个sha256函数。其结果是八个32位字，即32个字节。从它们中查找sha256很容易-调用了最终的sha256_transform（），一切就绪。请注意，输入数据比sha256_transform（）所需的64个字节小32个字节。因此，再次将块填充为零，并在末尾输入块长度。

总共只有3个对sha256_transform（）的调用，其中第一个必须只读取一次才能计算中间状态。

我试图将计算比特币块头的哈希值时发生的所有数据操作扩展到一个函数中，以便清楚地了解整个计算是如何专门针对比特币进行的，这就是发生的情况：

 //get bitcoin header via ptr to 80 bytes and calc hash template <typename T> void full_btc_hash(const uint8_t* ptr80, T nonce, T* presult) { //-1------------------------------------------ //init sha256 state s[7:0] T s[16]; for (int i = 0; i < 8; i++) { s[i] = sha256_init_state[i]; presult[i] = sha256_init_state[i]; } uint8_t tail2[] = { 0x80,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x01,0x00, }; uint32_t* p = (uint32_t*)tail2; for (int i = 0; i < 8; i++) { s[i + 8] = ntohl(p[i]); } //get first block for sha256 uint8_t tail[] = { /* 2nd sha256 block padding */ 0x80,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x02,0x80 }; T blk1[32]; p = (uint32_t*)ptr80; for (int i = 0; i < 19; i++) { blk1[i] = ntohl(p[i]); } //put nonce here blk1[19] = nonce; p = (uint32_t*)tail; for (int i = 0; i < 12; i++) { blk1[i + 20] = ntohl(p[i]); } sha256_transform(s, &blk1[0]); //warning! this can be called only once and produce MIDSTATE sha256_transform(s, &blk1[16]); sha256_transform(presult, s); }

我将此功能实现为c ++模板，它不仅可以对32位字（例如uint32_t）进行操作，而且可以以相同的方式对不同类型“ T”的字进行操作。我在这里，状态sha256被存储为“ T”类型的数组，并且通过指向“ T”类型数组的参数指针调用sha256_transform（），并且返回的结果相同。现在，转换函数也采用c ++模板的形式：

 template <typename T> T ror32(T word, unsigned int shift) { return (word >> shift) | (word << (32 - shift)); } template <typename T> T Ch(T x, T y, T z) { return z ^ (x & (y ^ z)); } template<typename T> T Maj(T x, T y, T z) { return (x & y) | (z & (x | y)); } #define e0(x) (ror32(x, 2) ^ ror32(x,13) ^ ror32(x,22)) #define e1(x) (ror32(x, 6) ^ ror32(x,11) ^ ror32(x,25)) #define s0(x) (ror32(x, 7) ^ ror32(x,18) ^ (x >> 3)) #define s1(x) (ror32(x,17) ^ ror32(x,19) ^ (x >> 10)) unsigned int ntohl(unsigned int in) { return ((in & 0xff) << 24) | ((in & 0xff00) << 8) | ((in & 0xff0000) >> 8) | ((in & 0xff000000) >> 24); } template <typename T> void LOAD_OP(int I, T *W, const u8 *input) { //W[I] = /*ntohl*/ (((u32*)(input))[I]); W[I] = ntohl(((u32*)(input))[I]); //W[I] = (input[3] << 24) | (input[2] << 16) | (input[1] << 8) | (input[0]); } template <typename T> void BLEND_OP(int I, T *W) { W[I] = s1(W[I - 2]) + W[I - 7] + s0(W[I - 15]) + W[I - 16]; } template <typename T> void sha256_transform(T *state, const T *input) { T a, b, c, d, e, f, g, h, t1, t2; TW[64]; int i; /* load the input */ for (i = 0; i < 16; i++) // MJ input is cast to u32* so this processes 16 DWORDS = 64 bytes W[i] = input[i]; /* now blend */ for (i = 16; i < 64; i++) BLEND_OP(i, W); /* load the state into our registers */ a = state[0]; b = state[1]; c = state[2]; d = state[3]; e = state[4]; f = state[5]; g = state[6]; h = state[7]; // t1 = h + e1(e) + Ch(e, f, g) + 0x428a2f98 + W[0]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x71374491 + W[1]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xb5c0fbcf + W[2]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xe9b5dba5 + W[3]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x3956c25b + W[4]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x59f111f1 + W[5]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x923f82a4 + W[6]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xab1c5ed5 + W[7]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xd807aa98 + W[8]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x12835b01 + W[9]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x243185be + W[10]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x550c7dc3 + W[11]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x72be5d74 + W[12]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x80deb1fe + W[13]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x9bdc06a7 + W[14]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xc19bf174 + W[15]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xe49b69c1 + W[16]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xefbe4786 + W[17]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x0fc19dc6 + W[18]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x240ca1cc + W[19]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x2de92c6f + W[20]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x4a7484aa + W[21]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x5cb0a9dc + W[22]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x76f988da + W[23]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x983e5152 + W[24]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xa831c66d + W[25]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xb00327c8 + W[26]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xbf597fc7 + W[27]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0xc6e00bf3 + W[28]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xd5a79147 + W[29]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x06ca6351 + W[30]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x14292967 + W[31]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x27b70a85 + W[32]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x2e1b2138 + W[33]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x4d2c6dfc + W[34]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x53380d13 + W[35]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x650a7354 + W[36]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x766a0abb + W[37]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x81c2c92e + W[38]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x92722c85 + W[39]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xa2bfe8a1 + W[40]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xa81a664b + W[41]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xc24b8b70 + W[42]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xc76c51a3 + W[43]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0xd192e819 + W[44]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xd6990624 + W[45]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0xf40e3585 + W[46]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x106aa070 + W[47]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x19a4c116 + W[48]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x1e376c08 + W[49]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x2748774c + W[50]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x34b0bcb5 + W[51]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x391c0cb3 + W[52]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x4ed8aa4a + W[53]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x5b9cca4f + W[54]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x682e6ff3 + W[55]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x748f82ee + W[56]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x78a5636f + W[57]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x84c87814 + W[58]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x8cc70208 + W[59]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x90befffa + W[60]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xa4506ceb + W[61]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0xbef9a3f7 + W[62]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xc67178f2 + W[63]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; state[0] += a; state[1] += b; state[2] += c; state[3] += d; state[4] += e; state[5] += f; state[6] += g; state[7] += h; }

使用C ++模板函数很方便，因为我可以根据常规数据计算所需的哈希值，并获得通常的结果：

  const uint8_t header[] = { 0x02,0x00,0x00,0x00, 0x17,0x97,0x5b,0x97,0xc1,0x8e,0xd1,0xf7, 0xe2,0x55,0xad,0xf2,0x97,0x59,0x9b,0x55, 0x33,0x0e,0xda,0xb8,0x78,0x03,0xc8,0x17, 0x01,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x8a,0x97,0x29,0x5a,0x27,0x47,0xb4,0xf1, 0xa0,0xb3,0x94,0x8d,0xf3,0x99,0x03,0x44, 0xc0,0xe1,0x9f,0xa6,0xb2,0xb9,0x2b,0x3a, 0x19,0xc8,0xe6,0xba, 0xdc,0x14,0x17,0x87, 0x35,0x8b,0x05,0x53, 0x53,0x5f,0x01,0x19, 0x48,0x75,0x08,0x33 }; uint32_t test_nonce = 0x48750833; uint32_t result[8]; full_btc_hash(header, test_nonce, result); uint8_t* presult = (uint8_t * )result; for (int i = 0; i < 32; i++) printf("%02X ", presult[i]);

原来：

92 98 2A 50 91 FA BD 42 97 8A A5 2D CD C9 36 28 02 4A DD FE E0 67 A4 78 00 00 00 00 00 00 00 00 00 00

在散列的末尾有许多零，一个漂亮的散列，宾果等。

现在，我不能将普通的uint32_t数据传递给此哈希函数，而是传递给我的特殊C ++类，该类将重新定义所有算法。

是的是的我将应用“替代”概率数学。
我自己发明，意识到，亲自体验。看来效果不是很好。开个玩笑它应该工作。也许我不是我要尝试的第一个。

现在我们转到最有趣的地方。
数字电子学中的所有算术都作为对位的运算来执行，并且严格由运算符AND，OR，NOT，EXCLUSIVE OR定义。好吧，我们都知道布尔代数中的真值表。

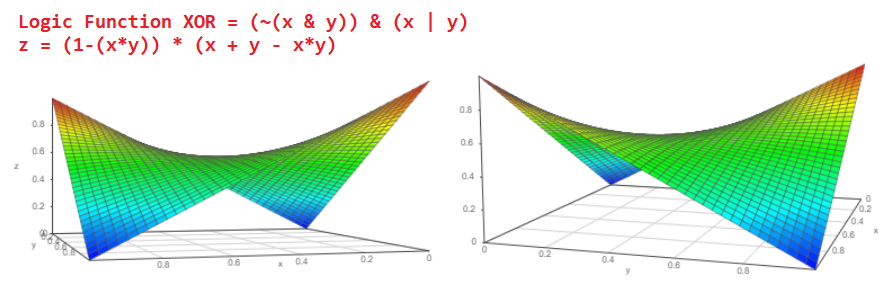
我建议给计算增加一些不确定性，使其具有概率性。
让单词中的每一位不仅具有可能的ZERO和ONE值，而且还具有所有中间值！我建议将位的值视为可能发生或可能不会发生的事件的概率。如果所有初始数据都是可靠已知的，则结果是可靠的。而且，如果有些数据缺乏，那么结果将很有可能出现。

实际上，假设有两个独立的事件“ a”和“ b”，其发生的概率自然是从零到一，分别是Pa和Pb。事件同时发生的可能性是多少？我相信我们每个人都会毫不犹豫地回答P = Pa * Pb，这是正确的答案！

从两个不同的角度来看，此类函数的3D图形将如下所示：

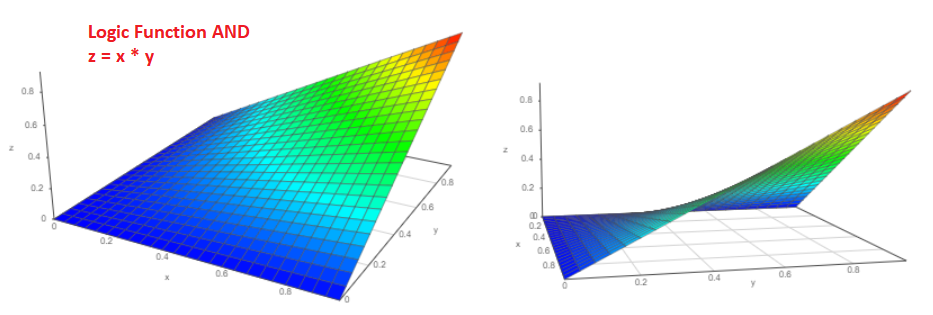
发生Pa事件或Pb事件的概率是多少？
概率P = Pa + Pb-Pa * Pb。功能图如下所示：

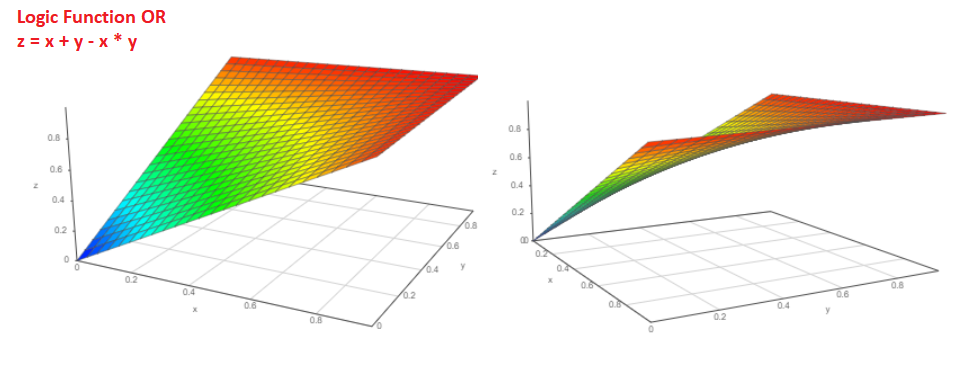
而且，如果我们知道事件Pa发生的可能性，那么该事件将不会发生的概率是多少？
P = 1-Pa。

现在让我们做一个假设。想象一下，我们有一些逻辑元素可以计算出输出事件的概率，而知道输入事件的概率：

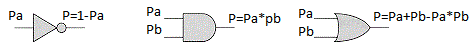
具有这样的逻辑元素可以很容易地使其变得更复杂，例如，异或或XOR：

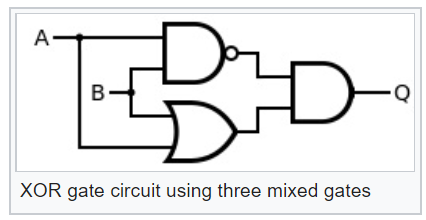
现在看一下这个XOR逻辑元素的图表，我们可以了解概率XOR输出处的事件概率为：

但这还不是全部。我们知道完全加法器的典型逻辑，并了解如何从完全加法器构成多位加法器：

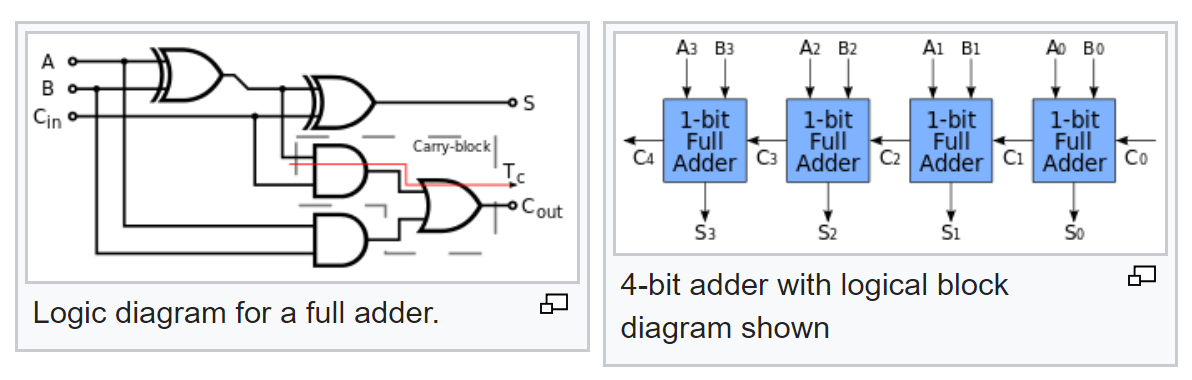
因此，现在，根据他的方案，我们现在可以在输入端具有已知信号概率的情况下计算其输出端的信号概率。

因此，我可以用概率算术在c ++中实现我自己的“ 32位”类（我将其称为x32），为所有AND，OR，XOR，ADD和shifts等sha256运算覆盖该类。该类将在内部存储32位，但是每个位都是一个浮点数。在这样的32位数字上的每个逻辑或算术运算将使用逻辑或算术运算的已知或鲜为人知的输入参数来计算每个位的值的概率。

考虑一个使用我的概率数学的非常简单的示例：

 typedef std::numeric_limits< double > dbl; int main(int argc, char *argv[]) { cout.precision(dbl::max_digits10); x32 a = 0xaabbccdd; x32 b = 0x12345678; <b>//b.setBit( 4, 0.75 );</b> x32 c = a + b; cout << std::hex << "result = 0x" << c.get32() << "\n" << std::dec; for (int i = 0; i < 32; i++) cout << "bit" << i << " = " << c.get_bvi(i) << "\n"; cout << "ok\n"; }

在此示例中，添加了两个32位数字。
而字符串是b.setBit（4，0.75）; 由于完全知道所有要输入的输入数据，因此将添加的结果注释为完全可预测和预定的注释。程序将其打印到控制台：

 result = 0xbcf02355 bit0 = 1 bit1 = 0 bit2 = 1 bit3 = 0 bit4 = 1 bit5 = 0 bit6 = 1 bit7 = 0 bit8 = 1 bit9 = 1 bit10 = 0 bit11 = 0 bit12 = 0 bit13 = 1 bit14 = 0 bit15 = 0 bit16 = 0 bit17 = 0 bit18 = 0 bit19 = 0 bit20 = 1 bit21 = 1 bit22 = 1 bit23 = 1 bit24 = 0 bit25 = 0 bit26 = 1 bit27 = 1 bit28 = 1 bit29 = 1 bit30 = 0 bit31 = 1

如果我取消注释b.setBit（4，0.75）行；那么我对程序说：“将这两个数字加到我身上，但我真的不知道第二个参数的第4位的值，我认为这是一个概率为0.75的数字。”

然后，通过对输出信号概率（即位）的完整计算，应有的加法发生：

 bit not stable bit not stable bit not stable result = 0xbcf02305 bit0 = 1 bit1 = 0 bit2 = 1 bit3 = 0 bit4 = 0.75 bit5 = 0.1875 bit6 = 0.8125 bit7 = 0 bit8 = 1 bit9 = 1 bit10 = 0 bit11 = 0 bit12 = 0 bit13 = 1 bit14 = 0 bit15 = 0 bit16 = 0 bit17 = 0 bit18 = 0 bit19 = 0 bit20 = 1 bit21 = 1 bit22 = 1 bit23 = 1 bit24 = 0 bit25 = 0 bit26 = 1 bit27 = 1 bit28 = 1 bit29 = 1 bit30 = 0 bit31 = 1

由于输入数据不是很知名，因此结果不是很知名。此外，可以可靠地计算出的被认为是可靠的。无法计数的被认为具有概率。

现在，我有了一个很棒的用于模糊算术的32位c ++类，我可以将x32类型的变量数组传递给模板中的full_btc_hash（）函数，并获得可能的估计哈希值。

一些x32类的实现是：

 #pragma once #include <string> #include <list> #include <iostream> #include <utility> #include <stdint.h> #include <vector> #include <limits> using namespace std; #include <boost/math/constants/constants.hpp> #include <boost/multiprecision/cpp_dec_float.hpp> using boost::multiprecision::cpp_dec_float_50; //typedef double MY_FP; typedef cpp_dec_float_50 MY_FP; class x32 { public: x32(); x32(uint32_t n); void init(MY_FP val); void init(double* pval); void setBit(int i, MY_FP val) { bvi[i] = val; }; ~x32() {}; x32 operator|(const x32& right); x32 operator&(const x32& right); x32 operator^(const x32& right); x32 operator+(const x32& right); x32& x32::operator+=(const x32& right); x32 operator~(); x32 operator<<(const unsigned int& right); x32 operator>>(const unsigned int& right); void print(); uint32_t get32(); MY_FP get_bvi(uint32_t idx) { return bvi[idx]; }; private: MY_FP not(MY_FP a); MY_FP and(MY_FP a, MY_FP b); MY_FP or (MY_FP a, MY_FP b); MY_FP xor(MY_FP a, MY_FP b); MY_FP bvi[32]; //bit values }; #include "stdafx.h" #include "x32.h" x32::x32() { for (int i = 0; i < 32; i++) { bvi[i] = 0.0; } } x32::x32(uint32_t n) { for (int i = 0; i < 32; i++) { bvi[i] = (n&(1 << i)) ? 1.0 : 0.0; } } void x32::init(MY_FP val) { for (int i = 0; i < 32; i++) { bvi[i] = val; } } void x32::init(double* pval) { for (int i = 0; i < 32; i++) { bvi[i] = pval[i]; } } x32 x32::operator<<(const unsigned int& right) { x32 t; for (int i = 31; i >= 0; i--) { if (i < right) { t.bvi[i] = 0.0; } else { t.bvi[i] = bvi[i - right]; } } return t; } x32 x32::operator>>(const unsigned int& right) { x32 t; for (unsigned int i = 0; i < 32; i++) { if (i >= (32 - right)) { t.bvi[i] = 0; } else { t.bvi[i] = bvi[i + right]; } } return t; } MY_FP x32::not(MY_FP a) { return 1.0 - a; } MY_FP x32::and(MY_FP a, MY_FP b) { return a * b; } MY_FP x32::or(MY_FP a, MY_FP b) { return a + b - a * b; } MY_FP x32::xor (MY_FP a, MY_FP b) { //(~(A & B)) & (A | B) return and( not( and(a,b) ) , or(a,b) ); } x32 x32::operator|(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = or ( bvi[i], right.bvi[i] ); } return t; } x32 x32::operator&(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = and (bvi[i], right.bvi[i]); } return t; } x32 x32::operator~() { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = not(bvi[i]); } return t; } x32 x32::operator^(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = xor (bvi[i], right.bvi[i]); } return t; } x32 x32::operator+(const x32& right) { x32 r; r.bvi[0] = xor (bvi[0], right.bvi[0]); MY_FP cout = and (bvi[0], right.bvi[0]); for (unsigned int i = 1; i < 32; i++) { MY_FP xor_a_b = xor (bvi[i], right.bvi[i]); r.bvi[i] = xor( xor_a_b, cout ); MY_FP and1 = and (bvi[i], right.bvi[i]); MY_FP and2 = and (xor_a_b, cout); cout = or (and1,and2); } return r; } x32& x32::operator+=(const x32& right) { MY_FP cout = and (bvi[0], right.bvi[0]); bvi[0] = xor (bvi[0], right.bvi[0]); for (unsigned int i = 1; i < 32; i++) { MY_FP xor_a_b = xor (bvi[i], right.bvi[i]); MY_FP and1 = and (bvi[i], right.bvi[i]); MY_FP and2 = and (xor_a_b, cout); bvi[i] = xor (xor_a_b, cout); cout = or (and1, and2); } return *this; } void x32::print() { for (int i = 0; i < 32; i++) { cout << bvi[i] << "\n"; } } uint32_t x32::get32() { uint32_t r = 0; for (int i = 0; i < 32; i++) { if (bvi[i] == 1.0) r = r | (1 << i); else if (bvi[i] == 0.0) { //ok } else { //oops.. cout << "bit not stable\n"; } } return r; }

这都是为了什么？

比特币矿工事先不知道选择32倍随机数的价值。矿工被迫对全部40亿个对象进行迭代，以便对哈希进行计数，直到它变得“美丽”为止，直到哈希值变得小于目标值为止。

理论上，模糊概率算法使您摆脱了详尽的搜索。

是的，我最初不知道所有必需的鼻子位的含义。如果我不认识它们，那就不要大惊小怪-无位的初始概率为0.5。即使在这种情况下，我也可以计算输出哈希位的概率。在某个地方，它们的结果也大约是0.5分钱或负半分钱。

但是，现在我只能将一个鼻子位从0.5更改为0.9或将0.1更改为1.0或更改为1.0，并查看输出中哈希函数每一位的信号值的概率值如何变化。现在，我有更多的评估信息。现在，我可以分别感觉到每个输入鼻子位，并观察哈希函数的每个输出位上信号的概率在哪里偏移。

例如，下面的代码片段考虑了一个哈希函数，该哈希函数具有完全未知的非比特，当其比特值的概率为0.5时，则进行第二次计算，假设随机数比特[0] = 0.9：

 typedef std::numeric_limits< double > dbl; int main(int argc, char *argv[]) { cout.precision(dbl::max_digits10); //--------------------------------- //hash: 502A989242BDFA912DA58A972836C9CDFEDD4A0278A467E00000000000000000 const u8 strxx[] = { 0x02,0x00,0x00,0x00, 0x17,0x97,0x5b,0x97,0xc1,0x8e,0xd1,0xf7, 0xe2,0x55,0xad,0xf2,0x97,0x59,0x9b,0x55, 0x33,0x0e,0xda,0xb8,0x78,0x03,0xc8,0x17, 0x01,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x8a,0x97,0x29,0x5a,0x27,0x47,0xb4,0xf1, 0xa0,0xb3,0x94,0x8d,0xf3,0x99,0x03,0x44, 0xc0,0xe1,0x9f,0xa6,0xb2,0xb9,0x2b,0x3a, 0x19,0xc8,0xe6,0xba, 0xdc,0x14,0x17,0x87, 0x35,0x8b,0x05,0x53, 0x53,0x5f,0x01,0x19, 0x48,0x75,0x08,0x33 }; double nonce_bits[32]; for (int i = 0; i < 32; i++) nonce_bits[i] = 0.5; x32 nonce_x32_a; x32 nonce_x32_b; nonce_x32_a.init(nonce_bits); nonce_bits[0] = 0.9; nonce_x32_b.init(nonce_bits); x32 result_x32_a[8]; x32 result_x32_b[8]; full_btc_hash(strxx, nonce_x32_a, result_x32_a); full_btc_hash(strxx, nonce_x32_b, result_x32_b); for (int i = 0; i < 32; i++) cout << result_x32_a[7].get_bvi(i) << " " << result_x32_b[7].get_bvi(i) << "\n";

类函数x32 :: get_bvi（）返回此数字的位值的概率。
我们进行了计算，发现如果将现时[0]位的值从0.5更改为0.9，则输出哈希的某些位几乎不会增加，而有些则几乎不会减少：

 0.44525679540883948 0.44525679540840074 0.55268174813167364 0.5526817481315932 0.57758654725359399 0.57758654725360606 0.49595026978928474 0.49595026978930477 0.57118578561406703 0.57118578561407746 0.53237003739057907 0.5323700373905661 0.57269859374138096 0.57269859374138162 0.57631236396381141 0.5763123639638157 0.47943176373960149 0.47943176373960219 0.54955992675177704 0.5495599267517755 0.53321116270879686 0.53321116270879733 0.57294025883744952 0.57294025883744984 0.53131857821387693 0.53131857821387655 0.57253530821899101 0.57253530821899102 0.50661432403287194 0.50661432403287198 0.57149419848354913 0.57149419848354916 0.53220327148366491 0.53220327148366487 0.57268927270412251 0.57268927270412251 0.57632130426913003 0.57632130426913005 0.57233970084776142 0.57233970084776143 0.56824728628552812 0.56824728628552813 0.45247155441889921 0.45247155441889922 0.56875940568326509 0.56875940568326509 0.57524323439326321 0.57524323439326321 0.57587726902392535 0.57587726902392535 0.57597043124557292 0.57597043124557292 0.52847748894672118 0.52847748894672118 0.54512141953055808 0.54512141953055808 0.57362254577539695 0.57362254577539695 0.53082194129771177 0.53082194129771177 0.54404489702929382 0.54404489702929382 0.54065386336136847 0.54065386336136847

一种微风，小数点后10m处退出的可能性几乎没有明显变化。好吧，不过...您可以尝试在此基础上进行一些假设。事实证明，是吧？

顺便说一句，如果输入鼻子的输入位是用正确的，必要的概率值初始化的，如下所示：

 double nonce_bits[32]; for (int i = 0; i < 32; i++) nonce_bits[i] = (real_nonce32&(1 << i)) ? 1.0 : 0.0; x32 nonce_x32; nonce_x32.init(nonce_bits); full_btc_hash(strxx, nonce_x32, result_x32);

然后计算概率哈希，我们得到逻辑上正确的结果-输出宾果游戏中的“美丽”哈希。

因此，有了数学，一切就在这里。

仍然有待学习如何分析微风的呼吸……并且散列被打破了。
听起来像废话，但这是废话-我在一开始就警告过。

其他有用的材料：

概率比特币挖掘方法

More articles: