大家好!
有一次,客户问我我的项目中是否有整数FFT,我一直在回答说,
别人已经以现成的,虽然弯曲但免费的IP核(Altera / Xilinx)的形式完成了-接受并使用它。 但是,这些核心
不是最佳的 ,具有一组“功能”,需要进一步完善。 就此而言,在我不想再度过平庸的另一个计划假期之后,我开始实现整数FFT的可配置内核。
 KDPV(调试数据溢出错误的过程)
KDPV(调试数据溢出错误的过程)在本文中,我想通过什么方法和手段告诉您在现代FPGA晶体上以整数格式计算快速傅里叶变换时可以实现数学运算。 任何FFT的基础都是一个称为“蝴蝶”的节点。 蝴蝶执行数学运算-加,乘和减。 故事将首先涉及“蝴蝶”及其最终节点的实现。 基于现代Xilinx FPGA系列-这是Ultrascale和Ultrascale +系列,以及旧系列6-(Virtex)和7-(Artix,Kintex,Virtex)都会受到影响。 现代项目中的较旧系列在2018年不再引起关注。 本文的目的是使用FFT的示例来揭示实现数字信号处理的自定义内核的功能。
引言
在数字信号处理工程师的一生中,采用FFT的算法已根深蒂固,这对任何人来说都不是秘密,因此始终需要此工具。 领先的FPGA制造商,例如Altera / Xilinx,已经具有灵活的可配置FFT / IFFT内核,但是它们具有许多局限性和功能,因此,我不得不多次使用自己的经验。 因此,这次我不得不根据FPGA上的Radix-2方案以整数格式实现FFT。 在
我的上一篇文章中,我已经以浮点格式
进行了FFT ,从那里您知道使用具有双重并行性的算法来实现FFT,也就是说,
内核可以以相同的频率处理两个复杂的样本 。 这是重要的FFT功能,在Xilinx FFT现成的内核中不可用。
示例:需要开发一个FFT节点,以800 MHz的频率对复数输入流进行连续操作。 Xilinx的内核不会解决这个问题(现代FPGA中可实现的处理时钟频率约为300-400 MHz),否则它将需要以某种方式抽取输入流。 使用定制内核,您无需事先干预即可以400 MHz的频率为两个输入采样提供时钟,而不是以800 MHz的频率为单个采样。
Xilinx FFT内核的另一个
缺点是无法以位反转顺序接受输入流 。 在这种连接上,要花费大量的FPGA芯片存储资源来按正常顺序重新排列数据。 对于信号快速卷积的任务,当两个FFT节点彼此靠在一起时,这可能成为关键时刻,也就是说,该任务根本不会位于所选的FPGA芯片中。 自定义FFT内核允许您以输入的正常顺序接收数据,并以位反转模式输出数据,而相反FFT的内核-相反,以位反转的方式接收数据,并以正常模式输出数据。 一次保存两个用于数据置换的缓冲区!
由于本文中的大多数内容都可能
与上一篇有所
重叠,因此 ,我决定专注于FPGA上整数格式的数学运算以实现FFT的主题。
FFT内核参数
- NFFT-蝴蝶数量(FFT长度),
- DATA_WIDTH-输入数据的位深度(4-32),
- TWDL_WIDTH-转向因子的位深度(8-27)。
- 系列 -定义在其上实现FFT的FPGA系列(“ NEW”-Ultrascale,“ OLD”-6/7 Xilinx FPGA系列)。
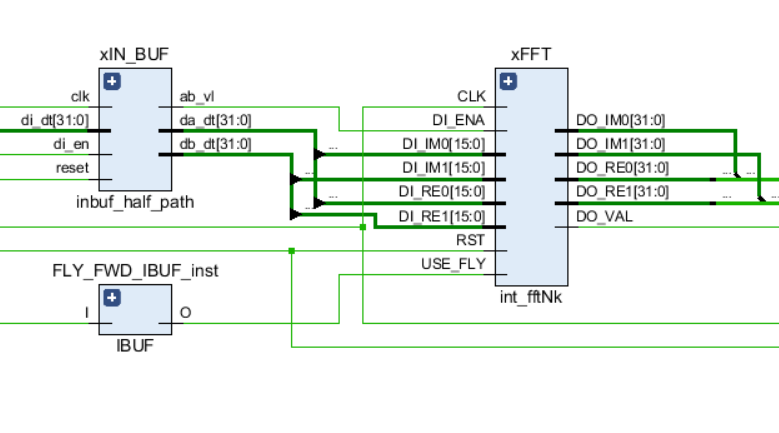
像电路中的任何其他链路一样,FFT具有输入控制端口-时钟信号和复位,以及输入和输出数据端口。 另外,内核中使用了USE_FLY信号,它使您可以动态关闭FFT蝶形以进行调试过程或查看原始输入流。
下表显示了使用的FPGA资源数量,具体取决于DATA_WIDTH = 16和两位TWDL_WIDTH = 16和24位的NFFT FFT的长度。

在Kintex-7晶体(410T)上,NFFT = 64K时的内核在处理频率
FREQ = 375 MHz时稳定。
项目结构
FFT节点的示意图如下图所示:

为了方便理解某些组件的功能,我将按层次结构顺序列出项目文件及其简短描述:
- FFT内核:
- int_fftNk -FFT节点,Radix-2电路,频率抽取(DIF),输入流正常,输出流位反转。
- int_ifftNk - OBPF节点,Radix-2电路,时间抽取(DIT),输入流为位反转,输出流为正常。
- 蝴蝶:
- int_dif2_fly-蝴蝶Radix-2,频率抽取,
- int_dit2_fly-蝴蝶Radix-2,及时抽取,
- 复数乘法器:
- int_cmult_dsp48-通用可配置乘数,包括:
- int_cmult18x25_dsp48-数据的小位深度和旋转因子的乘数,
- int_cmult_dbl18_dsp48-乘数增加了一倍,转折系数的位宽最大为18位,
- int_cmult_dbl35_dsp48-乘数加倍,旋转因子的位宽最大为25 *位,
- int_cmult_trpl18_dsp48-三重乘法器,转向因子的容量高达18位,
- int_cmult_trpl52_dsp48-三重乘法器,旋转因子的容量高达25 *位,
- 乘数:
- mlt42x18_dsp48e1-基于DSP48E1的操作数位最多为42和18位的乘法器,
- mlt59x18_dsp48e1-基于DSP48E1的操作数位最高为59和18位的乘法器,
- mlt35x25_dsp48e1-基于DSP48E1的操作数位最多为35和25位的乘法器,
- mlt52x25_dsp48e1-基于DSP48E1的操作数位最多为52和25位的乘法器,
- mlt44x18_dsp48e2-基于DSP48E2的操作数位最多为44和18位的乘法器,
- mlt61x18_dsp48e2-基于DSP48E2的操作数位最高为61和18位的乘法器,
- mlt35x27_dsp48e2-基于DSP48E2的操作数位最高为35和27位的乘法器,
- mlt52x27_dsp48e2是一个乘法器,基于DSP48E2的操作数位最多为52和27位。
- 累加器:
- int_addsub_dsp48-通用加法器,操作数位最多为96位。
- 延迟线:
- int_delay_line-延迟的基线,提供蝶形之间的数据排列,
- int_align_fft-输入数据与FFT蝶形输入处的转向因子的对齐,
- int_align_fft-输入数据和OBPF蝶形输入处的转向因子的对齐 ,
- 旋转因素:
- rom_twiddle_int-旋转因子的生成器,FFT从一定长度开始考虑基于DSP FPGA单元的系数,
- row_twiddle_tay-使用泰勒级数(NFFT> 2K)**的旋转因子生成器。
- 数据缓冲区:
- inbuf_half_path-输入缓冲区,在正常模式下接收流,并产生两个采样序列,其偏移量为FFT ***的一半,
- outbuf_half_path-输出缓冲区,收集两个序列并产生一个等于FFT长度的连续数,
- iobuf_flow_int2-缓冲区以两种模式工作:以Interleave-2模式接收流,并产生移位了一半长度的两个FFT序列。 反之亦然,取决于BITREV选项。
- int_bitrev_ord是一个简单的从自然顺序到位反转的数据转换器。
*-对于DSP48E1:25位,对于DSP48E2-27位。**-从FFT的某个阶段开始,可以使用固定数量的块存储器来存储旋转系数,并且可以使用DSP48节点使用泰勒公式对一阶导数计算中间系数。 由于内存资源对于FFT更为重要,因此可以为存储而安全地牺牲计算单元。
***-输入缓冲区和延迟线-对占用的FPGA内存资源量有重大贡献蝴蝶至少曾经遇到过快速傅立叶变换算法的每个人都知道,该算法基于基本操作-“蝴蝶”。 它通过将输入乘以旋转因子来转换输入流。 FFT有两种经典的转换方案-频率抽取(DIF,频率抽取)和时间抽取(DIT,时间抽取)。 DIT算法的特征是将输入序列分为两个半个持续时间的序列,DIF算法分成两个NFFT持续时间的偶数和奇数样本序列。 另外,这些算法在蝶形运算的数学运算上有所不同。
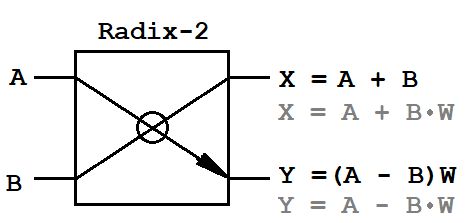 A,B-
A,B-输入复杂样本对,
X,Y-输出复杂样本对,
W-复杂的转向因素。
由于输入数据是复数,因此蝶形图需要一个复数乘法器(4个乘法运算和2个加法运算)和两个复数加法器(4个加法运算)。 这是必须在FPGA上实现的全部数学基础。
乘数
应该注意的是,FPGA上的所有数学运算通常都以附加代码(2的补码)执行。 FPGA乘法器可以通过两种方式实现-在使用触发器和LUT表的逻辑上,或者在特殊的DSP48计算单元上,它们已经被牢固地包含在所有现代FPGA中。 在逻辑块上,乘法是使用Booth算法或其修改实现的,占用了大量的逻辑资源,并且在高数据处理频率下并不总是满足时间限制。 在这方面,现代项目中的FPGA乘法器几乎总是基于DSP48节点设计的,偶尔仅基于逻辑设计的。 DSP48节点是完成数学和逻辑功能的复杂成品单元。 基本运算:乘法,加法,减法,累加,计数器,逻辑运算(XOR,NAND,AND,OR,NOR),平方,数比较,移位等。 下图显示了Xilinx Ultrascale + FPGA系列的DSP48E2单元。

通过输入端口的简单配置,节点中的计算操作以及节点内部的延迟设置,您可以制作高速数学数据脱粒机。
请注意,开发环境中的所有顶级FPGA供应商都具有标准和免费IP内核,用于基于DSP48节点计算数学函数。 它们使您可以计算原始的数学函数,并在节点的输入和输出上设置各种延迟。 对于Xilinx,这是IP核“乘法器”(12.0版,2018年),可让您将乘法器配置为2到64位输入数据的任何位深度。 此外,您可以指定如何在逻辑资源或内置DSP48原语上实现乘法器。
用端口A和B上输入数据的位深度
估计乘数“吃”多少逻辑 = 64位。 如果使用节点DSP48,则它们仅需要16个。

DSP48单元的主要限制是输入数据的位深度。 节点DSP48E1是FPGA Xilinx 6和7系列的基本单元,用于乘法运算的输入端口的宽度为:“ A”-25位,“ B”-18位,因此,乘法结果为43位数字。 对于Xilinx Ultrascale和Ultrascale + FPGA系列,该节点进行了几处更改,特别是第一个端口的容量增加了两位:“ A”-27位,“ B”-18-位。 另外,该节点本身称为DSP48E2。
为了不依赖于特定的系列和FPGA芯片,以确保“源代码的纯度”,并考虑输入数据的所有可能的位深度,决定设计自己的乘法器集。 这将允许最有效地实现FFT蝶形的复数乘法器,即基于DSP48块的乘法器和加减法器。 乘法器的第一个输入是输入数据,乘法器的第二个输入是旋转因子(来自存储器的谐波信号)。 使用内置的UNISIM库可实现一组乘法器,从中必须连接DSP48E1和DSP48E2原语,以便在项目中进一步使用它们。 表格中显示了一组乘数。 应该注意的是:
- 乘数运算导致乘积的容量与操作数的容量之和增加。
- 实际上,每个乘法器25x18和27x18是重复的-这是不同系列的一个组件。
- 操作的并行化阶段越大,计算的延迟就越大,占用的资源越多。
- 如果输入“ B”的位深度较低,则可以实现另一输入的位深度较高的乘法器。
- 端口“ B”(DSP48基元的实际端口)和内部移位寄存器都增加了17位,这是增加位深度的主要限制。
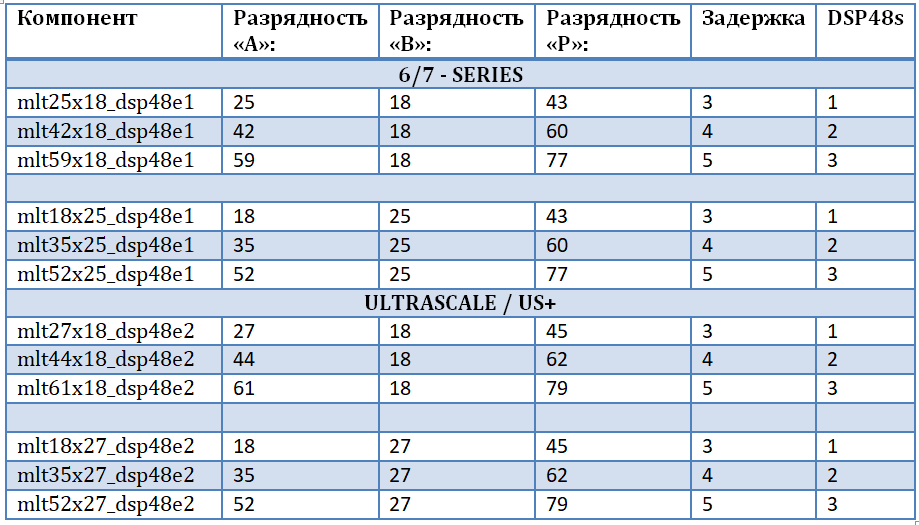
由于以下原因,在任务框架中不再关注位深度的进一步增加:
车削系数的位深
众所周知,谐波信号的分辨率越高,数字出现越准确(分数部分的符号越多)。 但是端口位的大小为B <25位,这是因为对于FFT节点中的旋转因子而言,该位深度足以确保“蝴蝶”中输入流与谐波信号元素的高质量相乘(对于现代FPGA上任何可实际实现的FFT长度)。 在我正在执行的任务中,转弯系数的位深度的典型值为16位,24位-很少出现32位-从不。
输入样本的位深度
这些典型的接收和记录节点(ADC,DAC)的容量不大-从8位到16位,很少-24位或32位。 此外,在后一种情况下,使用符合IEEE-754标准的浮点数据格式更为有效。 另一方面,由于数学运算,FFT中“蝴蝶”的每一级都会向输出样本中添加一位数据。 例如,对于NFFT = 1024的长度,使用log2(NFFT)= 10个蝶形。
因此,输出位深度将比输入大10位,WOUT = WIN +10。通常,公式如下所示:
WOUT = WIN + log2(NFFT);
一个例子:
输入流WIN的位深度= 32位,
转向因子TWD的位深度= 27,
本文实现的乘法器列表中的端口“ A”的容量不超过52位。 这意味着蝶形的最大数量为FFT = 52-32 =20。即,可以实现长度不超过2 ^ 20 = 1M个样本的FFT。 (但是,实际上,由于资源有限,即使对于功能最强大的FPGA晶振,这也无法通过直接方式实现,但这与另一个主题有关,因此本文中将不予考虑。)
如您所见,这是为什么我没有实现具有较高输入端口位深度的乘法器的主要原因之一。
用于计算整数FFT
的乘法器覆盖了所需输入
位大小和旋转因子
的全部范围 。 在所有其他情况下,您都可以
以浮点格式使用
FFT计算!
执行“宽”乘数
基于一个简单的示例,该示例将两个不符合标准DSP48节点位深的数字相乘,我将展示如何实现宽数据乘法器。 下图显示了其框图。 乘法器在附加代码中实现两个有符号数的乘法,第一个操作数X的宽度为42位,第二个Y为18位。 它包含两个DSP48E2节点。 两个寄存器用于均衡上层节点中的延迟。 这样做是因为在上位加法器中,您需要正确地添加来自DSP48的上,下节点的数字。 底部加法器未实际使用。 在下层节点的输出处,会有乘积的附加延迟,以使输出编号与时间对齐。 总延迟为4个周期。

这项工作包括两个部分:
- 最年轻的部分: P1 ='0'&X [16:0] * Y [17:0];
- 较旧的部分: P2 = X [42:17] * Y [17:0] +(P1 >> 17);
累加器
像乘法器一样,加法器可以使用传输链在逻辑资源上或在DSP48模块上构建。 为了获得最大的吞吐量,第二种方法是优选的。 一个DSP48原语允许实现最多48位的加法运算,两个节点最多96位的加法运算。 对于当前任务,这样的位深度已足够。 此外,DSP48原语具有特殊的“ SIMD MODE”模式,该模式将内置的48位ALU并行化为具有不同容量小数据的几种操作。 也就是说,在“一个”模式下,使用48位的完整位网格和两个操作数,在“两个”模式下,将位网格划分为每个24位的几个并行流(4个操作数)。 此模式仅使用一个加法器,有助于减少输入采样的小比特深度(在计算的第一阶段)所占用的FPGA芯片资源。
位深度增加
在二进制附加码中将两个数字与位N和M
相乘会导致输出位容量增加到
P = N +M。示例:将三位数N = M = 3乘以,最大正数为+3 =
(011) 2 ,最大负数为4 =
(100) 2 。 最高有效位负责数字的符号。 因此,相乘时的最大可能数为+16 =
(010000) 2 ,这是通过将两个最大负数-4相乘而形成的。 输出的位深度等于输入位的总和P = N + M = 6位。
将二进制附加代码中的N和M位与两个数字
相加的操作导致输出位增加一位。
示例:添加两个正数,N = M = 3,最大正数为3 =
(011) 2 ,最大负数为4 =
(100) 2 。
最高有效位负责数字的符号。因此,最大正数为6 = (0110)2,最大负数为-8 = (1000)2。输出分辨率提高一位。考虑算法特征
从上方截断位深度:为了最大程度地减少FFT算法中的FPGA资源,已决定,在蝶形数据相乘时,切勿使用最大可能的负数作为转折系数。该修正案不会对结果产生不利影响。例如,当使用旋转因子的16位表示形式时,最小值为-32768 = 0x8000,下一个为-32767 = 0x8001。用最近的邻近值替换最大负数时的错误约为0.003%,完全可以接受。通过删除两个数字的乘积中的最小数字,可以在每次迭代中减少一个未使用的高阶位。示例:数据-4 =(100) 2,系数+3 =(011) 2。乘法结果= -12 =(110100)2。可以丢弃第五位,因为它复制了邻居,第四个是符号位。从下面截断位:显然,将“蝴蝶”中的输入信号乘以谐波效果,没有必要将输出位深度拉到下一个蝶形中,但是需要四舍五入或截断。旋转因子以方便的M位格式表示,但实际上,它是正常的正弦和余弦,归一化为单位。也就是说,数字0x8000 = -1,数字0x7FFF = +1。因此,相乘的结果必须被截断到数据的原始位深度(即,来自旋转因子的M位从底部被截断)。在我偶然看到的所有FFT实现中,通过一种或另一种方式将转折因子归一化为1。因此,从相乘结果来看,有必要采用以下网格中的位[N + M-1-1:M-1]。最高有效位未使用(减去额外的1),最低有效位被截断。不会以任何方式最小化“蝴蝶”操作中数据的加/减,并且仅此操作有助于在计算的每个阶段将输出数据的位深度增加一位。请注意,在FFT DIT算法的第一阶段或FFT DIF算法的最后阶段,必须将数据乘以零系数W0 = {Re,Im} = {1,0}的转折因子。由于乘以零和零是原始运算,因此可以将其省略。在这种情况下,根本不需要复数乘法运算:实部和虚部都会经历“转弯”而不会发生变化。在第二阶段,使用两个系数:W0 = {Re,Im} = {1,0}和W1 = {Re,Im} = {0,-1}。类似地,可以将操作简化为基本转换,并使用多路复用器选择输出样本。这使您可以在前两个蝶形上大大节省DSP48模块。复数乘法器的构造类似-基于乘法器和加减法器,但是,对于输入数据位深度的某些选项,不需要额外的资源,下面将对此进行描述。输入缓冲器和延迟线以及交叉开关与上一篇文章中描述的类似。旋转因子变为整数,可配置位深度。否则,FFT内核的设计不会有全局变化。FFT核心功能INT_FFTK
- 全流水线数据处理方案。
- NFFT转换长度= 8-512K点。
- 灵活调整NFFT转换长度。
- 整数输入格式,位宽是可配置的。
- 旋转因子的整数格式,位宽是可配置的。
- .
- !
- .
- : – , -.
- : - , – .
- . Radix-2.
- NFFT *.
- .
- (Virtex-6, 7-Series, Ultrascale).
- ~375MHz Kintex-7
- – VHDL.
- bitreverse +.
- 开源项目,不包含第三方IP内核。
源代码
我在github上的个人资料中可以找到 VHDL上FFT INTFFTK内核的源代码(包括基本运算和一组乘法器)以及Matlab / Octave的m脚本。结论
在开发过程中,设计了一个新的FFT核,与同行相比,该核提供了更高的性能。FFT和OBPF内核的组合不需要转换为自然顺序,并且最大转换长度仅受FPGA资源限制。双并发允许您处理IP-CORE Xilinx无法做到的双频输入流。整数FFT输出的位深度根据转换级数线性增加。在上一篇文章中,我写了有关未来的计划:FFT核心Radix-4,Radix-8,用于数百万点的超长FFT,FFT-FP32(采用IEEE-754格式)。简而言之,几乎所有内容都被允许,但出于某种原因或其他原因,目前无法将它们公开。例外是FFT Radix-8算法,我什至没有(麻烦和懒惰)。我再次感谢dsmv2014,她一直欢迎我的冒险想法。感谢您的关注!
更新2018/08/22
在源代码中添加了SCALED FFT / IFFT选项。在每只蝶形上,位深度都被截断1位(截断LSB)。输出位深度=输入位深度。另外,我将给出真实信号通过FPGA的两个图形,以显示转换的整体属性,即:截断如何影响FFT输出上误差累积的结果。从理论上知道,由于傅里叶变换,当输入信号相对于非截断版本被截断时,信噪比变差。示例:输入幅度的幅度为6位。该信号是128 PF采样时的正弦波。NFFT = 1024个样本,DATA_WIDTH = 16,TWDL_WIDTH = 16。FFT信号通过的两个图表图 1信噪比很弱: 图 2信噪比强:
图 2信噪比强:
如您所见,SCALED选项没有从噪声中“拉出”正弦波,而UNSCALED选项则显示出良好的效果。