求职面试算法概述-集生成

哈Ha！

这篇文章根据大型IT公司（Mail.Ru Group，Google等）喜欢给候选人进行面试的算法开始分析任务（如果对算法的面试不好，那么有机会在梦想中的公司工作的机会）趋于零）。 首先，对于那些没有奥林匹克编程经验或不熟悉ShAD或LKS等繁重课程（对算法主题的重视程度很高）的人，或者对于那些想在某个领域重新学习知识的人，这篇文章非常有用。

同时，不能说在访谈中一定会满足这里要处理的所有任务，但是，解决这些任务的方法在大多数情况下是相似的。

叙述将分为不同的主题，我们将从生成具有特定结构的集合开始。

1.让我们从按钮手风琴开始：您需要使用相同类型的方括号（ 正确的方括号序列 ）生成所有正确的方括号序列（方括号个数为k）。

这个问题可以通过几种方式解决。 让我们从递归开始。

此方法假定我们开始对空列表中的序列进行迭代。 将方括号（打开或关闭）添加到列表中之后，再次执行递归调用并检查条件。 有什么条件 有必要监视cnt括号和右方括号（ cnt变量）之间的差异-如果该差异不是正数，则不能在列表中添加右方括号，否则括号顺序将不再正确。 仍然需要在代码中仔细实现。

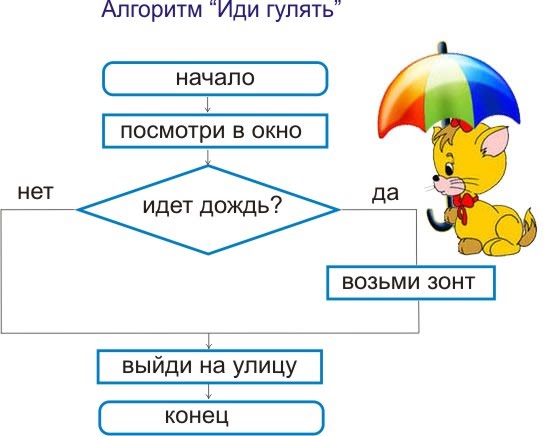
 k = 6 #   init = list(np.zeros(k)) #  ,    cnt = 0 #    ind = 0 # ,       def f(cnt, ind, k, init): #  . ,     if (cnt <= k-ind-2): init[ind] = '(' f(cnt+1, ind+1, k, init) # .    ,  cnt > 0 if cnt > 0: init[ind] = ')' f(cnt-1, ind+1, k, init) #      if ind == k: if cnt == 0: print (init) 

该算法的复杂度为 $$$O（（C_k ^ {k / 2}-C_k ^ {k / 2 -1}）* k）$需要额外的内存 $$$O（k）$。

使用给定的参数，函数调用 $$$f（cnt，ind，k，init）$将输出以下内容：

解决此问题的一种迭代方法：在这种情况下，想法将根本不同-您需要为括号序列引入字典顺序的概念。

考虑到以下事实，可以对一种类型的所有正确的括号序列进行排序： $$$'（'<'）'$。 例如，对于n = 6，按字典顺序，最低的序列是 $$$（（（）））$和最古老的- $$$（）（）（）$。

要获得下一个词典顺序，您需要找到最右边的右括号，在该括号之前有一个右括号，以便当将它们交换到位时，括号顺序保持正确。 我们将它们交换，使后缀成为最大的字典上的次要字母-为此，您需要在每一步中计算括号数量之间的差。

在我看来，这种方法比递归稍微麻烦一些，但是可以用来解决生成集的其他问题。 我们在代码中实现了这一点。

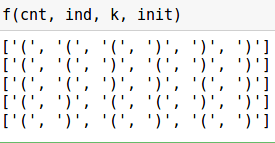
 #  ,    n = 6 arr = ['(' for _ in range(n//2)] + [')' for _ in range(n//2)] def f(n, arr): #    print (arr) while True: ind = n-1 cnt = 0 #  . ,    while ind>=0: if arr[ind] == ')': cnt -= 1 if arr[ind] == '(': cnt += 1 if cnt < 0 and arr[ind] =='(': break ind -= 1 #   ,     if ind < 0: break #   .  arr[ind] = ')' #      for i in range(ind+1,n): if i <= (n-ind+cnt)/2 +ind: arr[i] = '(' else: arr[i] = ')' print (arr) 

该算法的复杂度与前面的示例相同。

顺便说一句，有一个简单的方法证明了给定n / 2生成的括号序列的数量必须与加泰罗尼亚数匹配。

有效！

太好了，现在有了括号，让我们继续生成子集。 让我们从一个简单的难题开始。

2.给定一个升序数组，数字从 $$$0$之前 $$$n-1$，则需要生成其所有子集。

请注意，此类集合的子集数量恰好是 $$$2 ^ n$。 如果每个子集都表示为索引数组，则其中 $$$0$表示该元素不包含在集合中，但是 $$$1$-包括什么，那么所有此类数组的生成将是所有子集的生成。

如果考虑从0到0的数字的按位表示 $$$2 ^ n-1$，那么他们将指定所需的子集。 即，为了解决该问题，必须对二进制数实施单位加法。 我们从全零开始，到一个有一个单位的数组结束。

 n = 3 B = np.zeros(n+1) #  B   1  (    ) a = np.array(list(range(n))) #   def f(B, n, a): #   while B[0] == 0: ind = n #     while B[ind] == 1: ind -= 1 #   1 B[ind] = 1 #      B[(ind+1):] = 0 print (a[B[1:].astype('bool')]) 

该算法的复杂度为 $$$O（n * 2 ^ n）$，从内存中- $$$O（n）$。

现在让我们稍微复杂一些以前的任务。

3.给定一个升序排列的有序数组，数字从 $$$0$之前 $$$n-1$，您需要生成所有这些 $$$k$-element子集（迭代求解）。

我注意到，此问题的表述与上一个问题类似，可以使用大致相同的方法来解决： $$$k$单位和 $$$n-k$零，然后按顺序排序这些长度序列的所有变体 $$$n。$

但是，需要进行较小的更改。 我们需要整理一切 $$$k$的值集 $$$0$之前 $$$n-1$。 您需要确切了解如何对子集进行排序。 在这种情况下，我们可以为此类集合引入字典顺序的概念。

我们还按字符代码排列顺序： $$$1 <0$（这当然很奇怪，但这是必要的，现在我们将了解原因）。 例如，对于 $$$n = 4，k = 2$最小和最大的顺序 $$$[1,1,0,0]$和 $$$[0,0,1,1]$。

仍然有待了解如何描述从一个序列到另一个序列的过渡。 一切都很简单：如果我们改变 $$$1$在 $$$0$，然后在左侧，我们在考虑到条件保留的前提下写了最小词典编纂 $$$k$。 代码：

 n = 5 k = 3 a = np.array(list(range(n))) #    k -   init = [1 for _ in range(k)] + [0 for _ in range(nk)] def f(a, n, k, init): #   k-  print (a[a[init].astype('bool')]) while True: unit_cnt = 0 cur_ind = 0 #   ,     1 while (cur_ind < n) and (init[cur_ind]==1 or unit_cnt==0): if init[cur_ind] == 1: unit_cnt += 1 cur_ind += 1 #        -    if cur_ind == n: break #  init[cur_ind] = 1 #   . .  for i in range(cur_ind): if i < unit_cnt-1: init[i] = 1 else: init[i] = 0 print (a[a[init].astype('bool')]) 

工作示例：

该算法的复杂度为 $$$O（C_n ^ k * n）$，从内存中- $$$O（n）$。

4.给定一个升序数组，数字从 $$$0$之前 $$$n-1$，您需要生成所有这些 $$$k$-element子集（递归求解）。

现在让我们尝试递归。 想法很简单：这次没有描述，请参见代码。

 n = 5 a = np.array(list(range(n))) ind = 0 # ,       num = 0 # ,       k = 3 sub = list(-np.ones(k)) #  def f(n, a, num, ind, k, sub): #   k  ,     if ind == k: print (sub) else: for i in range(n - num): #  ,      k  if (n - num - i >= k - ind): #      sub[ind] = a[num + i] #     f(n, a, num+1+i, ind+1, k, sub) 

工作示例：

复杂度与以前的方法相同。

5.给定一个升序数组，数字从 $$$0$之前 $$$n-1$，则需要生成其所有排列。

我们将解决使用递归的问题。 该解决方案类似于上一个解决方案，在该解决方案中有一个辅助列表。 如果启用，则初始为零 $$$我$元素的第四位是单位，则元素 $$$我$已经在排列中。 快做决定：

 a = np.array(range(3)) n = a.shape[0] ind_mark = np.zeros(n) #   perm = -np.ones(n) #     def f(ind_mark, perm, ind, n): if ind == n: print (perm) else: for i in range(n): if not ind_mark[i]: #     ind_mark[i] = 1 #   perm[ind] = i f(ind_mark, perm, ind+1, n) #   -    ind_mark[i] = 0 

工作示例：

该算法的复杂度为 $$$O（n ^ 2 * n！）$，从内存中- $$$O（n）$

现在考虑格雷码的两个非常有趣的难题。 简而言之，这是一组长度相同的序列，其中每个序列在一个类别中与其邻居不同。

6.生成长度为n的所有二维格雷码。

解决这个问题的想法很酷，但是如果您不知道解决方案，那么可能很难想到。 我注意到这些序列的数量是 $$$2 ^ n$。

我们将迭代解决。 假设我们生成了此类序列的一部分，并且它们位于某个列表中。 如果我们复制这样一个列表并以相反的顺序写入，则第一个列表中的最后一个序列与第二个列表中的第一个序列重合，倒数第二个与第二个列表重合，依此类推。 将这些列表合并为一个。

为了使列表中的所有序列在同一类别中彼此不同，需要做什么？ 将一个单位放在第二个列表的元素中的适当位置，以获取格雷码。

很难被“耳朵”感知；我们将描述该算法的迭代。

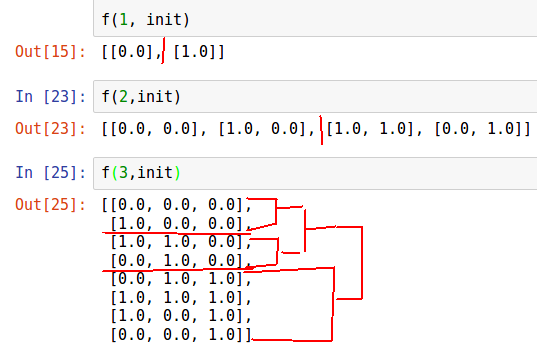
 n = 3 init = [list(np.zeros(n))] def f(n, init): for i in range(n): for j in range(2**i): init.append(list(init[2**i - j - 1])) init[-1][i] = 1.0 return init 

此任务的复杂性是 $$$O（n * 2 ^ n）$，从内存相同。

现在，让任务复杂化。

7.生成长度为n的所有k维格雷码。

显然，过去的任务只是该任务的特例。 但是，以解决过去任务的优美方式，这是无法解决的；这里有必要以正确的顺序整理序列。 让我们得到一个二维数组 $$$k * n$。 最初，最后一行具有单位，其余的具有零。 而且，在矩阵中 $$$-1$。 在这里 $$$1$和 $$$-1$在方向上彼此不同： $$$1$点向上 $$$-1$点下来。 重要提示：任何时候，每一列只能有一个 $$$1$或 $$$-1$，其余数字将为零。

现在我们将了解如何整理出这些序列以获得格雷码。 从头开始，向上移动元素。

下一步，我们达到顶峰。 我们写出结果序列。 达到限制后，您需要开始处理下一列。 您需要从右到左寻找它，如果找到可以移动的列，那么对于所有无法使用的列，箭头将朝相反的方向更改，以便可以再次移动它们。

现在您可以将第一列向下移动。 我们将其移动到地面。 依此类推，直到所有箭头射到地板或天花板上，并且没有剩余的列可以移动。

但是，在内存节省的框架中，我们将使用两个一维长度数组来解决此问题。 $$$n$：在一个数组中序列的元素本身将位于，而在另一个方向（箭头）。

 n,k = 3,3 arr = np.zeros(n) direction = np.ones(n) #   ,    def k_dim_gray(n,k): #    print (arr) while True: ind = n-1 while ind >= 0: #    ,    if (arr[ind] == 0 and direction[ind] == 0) or (arr[ind] == k-1 and direction[ind] == 1): direction[ind] = (direction[ind]+1)%2 else: break ind -= 1 #     ,     if ind < 0: break #    1 ,   1  arr[ind] += direction[ind]*2 - 1 print (arr) 

工作示例：

该算法的复杂度为 $$$O（n * k ^ n）$，从内存中- $$$O（n）$。

通过归纳证明该算法的正确性。 $$$n$，这里我将不描述证据。

在下一篇文章中，我们将分析动态任务。