🛀🏾 🚶🏿 🤙🏻 定积分的计算：基本算法 🕸️ 🗜️ 👼🏾

该出版物描述了用于计算段上一个变量的函数积分的最简单方法，也称为正交公式。通常，这些方法是在标准数学库中实现的，例如用于C的GNU科学库，用于Python的SciPy等。该出版物旨在证明这些方法如何“在幕后”工作，并引起人们对算法准确性和性能的关注。我还要指出正交公式与普通微分方程数值积分方法的关系，对此我要写另一本出版物。

积分的定义

函数的积分（根据Riemann） $f（x）$ 在细分市场上 $[a; b]$ 以下限制称为：

（ ） 到 （ ） （ ） ， 〜 〜 （ ）

$\ int_a ^ bf（x）dx = \ lim _ {\ Delta x \到0} \ sum_ {i = 0} ^ {n-1} f（\ xi_i）（x_ {i + 1}-x_i），〜〜（1）$

在哪里 $\ Delta x = \ max \ lbrace x_ {i + 1}-x_i \ rbrace$ -隔板的细度， $x_0 = a$ ， $x_n = b$ ， $\ xi_i$ -段上的任意数字 $[x_i; x_ {i + 1}]$ 。

如果函数的积分存在，则限制值是相同的，而与分区无关，只要它足够小即可。

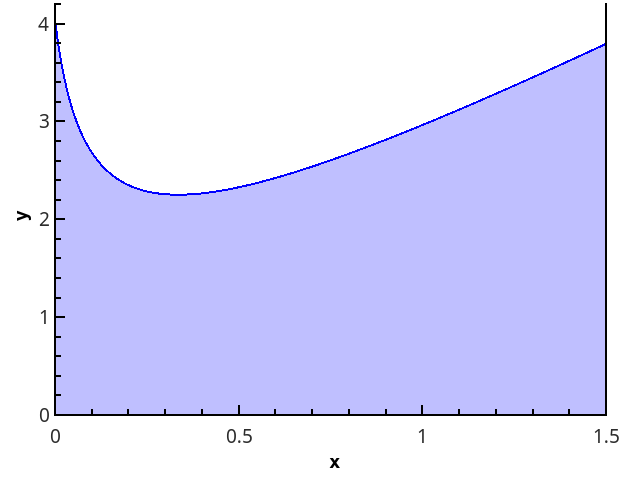
几何定义更清晰-积分等于以0 x轴，函数图以及直线x = a和x = b （图中的填充区域）为边界的弯曲梯形的面积。

正交公式

整数（1）的定义可以用以下形式重写

$I = \ int_a ^ b f（x）dx \大约I_n =（b-a）\ sum_ {i = 0} ^ {n-1} w_i f（\ xi_i），~~（2）$

在哪里 $w_i$ -权重系数（其总和应等于1）和系数本身-随数字增加趋于零 $n$ 计算函数的点。

表达式（2）是所有正交公式（即，用于积分的近似计算的公式）的基础。挑战在于选择要点 $\ lbrace \ xi_i \ rbrace$ 和重量 $w_i$ 因此右侧的总和尽可能精确地接近所需积分。

计算任务

功能集 $f（x）$ 为此，有一种算法可以计算间隔中任意点的值 $[a; b]$ （我的意思是用浮点数表示的点-那里没有Dirichlet函数！）。

需要找到积分的近似值 $\ int_a ^ b f（x）dx$ 。
该解决方案将在Python 3.6中实现。

要检查方法，请使用积分 $\ int_0 ^ {3/2} \左[2x + \ frac {1} {\ sqrt {x + 1/16}} \右] dx = 17/4$ 。

分段常数逼近

理想的简单正交公式来自表达式“ 1”在“额头中”的应用：

$I_n = \ sum_ {i = 0} ^ {n-1} f（\ xi_i）（x_ {i + 1}-x_i）$

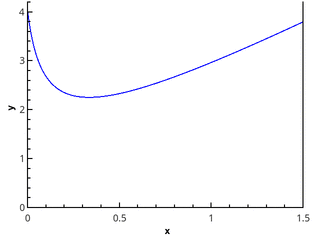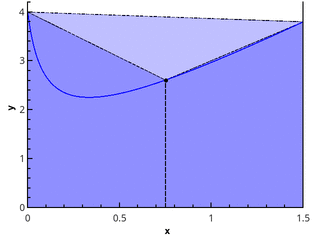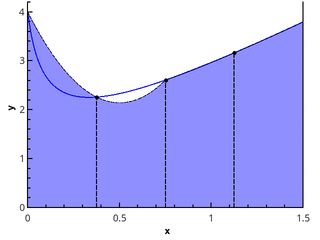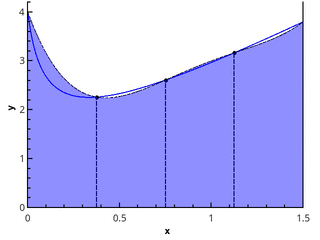
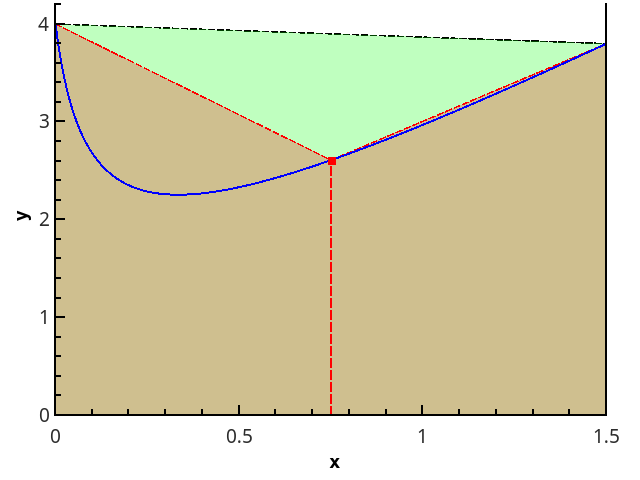
因为从分割点的方法 $\ lbrace x_i \ rbrace$ 然后选择点 $\ lbrace \ xi_i \ rbrace$ 极限值不依赖于此，那么我们选择它们以便可以方便地进行计算-例如，我们统一划分分区，对于函数的计算点，我们考虑以下选项：1） $\ xi_i = x_i$ ; 2） $\ xi_i = x_ {i + 1}$ ; 3） $\ xi_i =（x_i + x_ {i + 1}）/ 2$ 。

我们分别得到左矩形，右矩形和带有中点的矩形的方法。

实作

def _rectangle_rule(func, a, b, nseg, frac): """  .""" dx = 1.0 * (b - a) / nseg sum = 0.0 xstart = a + frac * dx # 0 <= frac <= 1    , #    , #     dx for i in range(npoints): sum += func(xstart + i * dx) return sum * dx def left_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, nseg, 0.0) def right_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, npoints, 1.0) def midpoint_rectangle_rule(func, a, b, nseg): """    """ return _rectangle_rule(func, a, b, nseg, 0.5)

为了分析正交公式的性能，我们在坐标图中构造了一个误差图：“点数是数值结果与精确数值之间的差”。

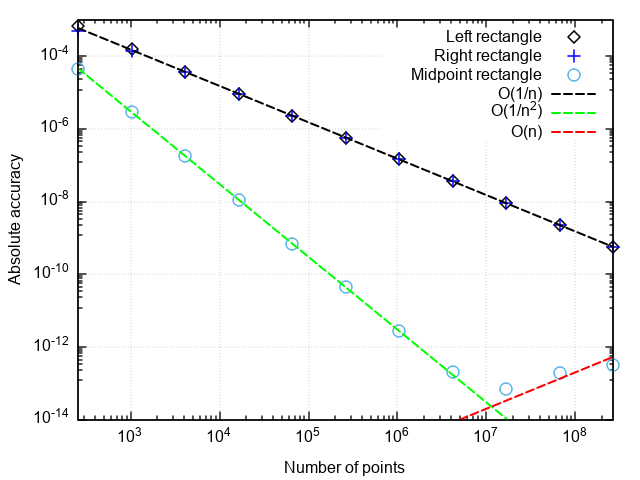
您会注意到：

具有中点的公式比具有右点或左点的公式准确得多
带有中点的公式的误差下降速度快于其他两个
如果分区很小，则带有中点的公式的误差开始增加
前两点与以下事实有关：具有中点的矩形公式具有第二个逼近阶，即 $| I_n-I | = O（1 / n ^ 2）$ ，左右矩形的公式为一阶，即 $| I_n-I | = O（1 / n）$ 。
当对大量项求和时，积分步骤的磨削过程中误差的增加与舍入误差的增加相关。这个错误会像 $| I_n-I | = O（1 / n）$ 不允许集成来实现机器精度。
结论：具有左右两边的矩形的方法精度较低，并且随着分区的细化而缓慢增长。因此，它们仅出于演示目的。具有中点的矩形方法具有较高的近似阶数，这使其有机会在实际应用中使用（更多内容请参见下文）。

分段线性逼近

下一步的逻辑步骤是通过线性函数逼近每个子段上的可积函数，该函数给出梯形的正交公式：

$I_n = \ sum_ {i = 0} ^ {n-1} \ frac {f（x_i）+ f（x_ {i + 1}）} {2}（x_ {i + 1}-x_i）~~（ 3）$

n = 1和n = 2的梯形方法的图示。

在均匀网格的情况下，分区的所有段的长度相等，并且公式的形式为

$I_n = h \左（\ frac {f（a）+ f（b）} {2} + \ sum_ {i = 1} ^ {n-1} f（a + ih）\ right），〜h = \ frac {ba} {n} ~~（3a）$

实作

 def trapezoid_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" dx = 1.0 * (b - a) / nseg sum = 0.5 * (func(a) + func(b)) for i in range(1, nseg): sum += func(a + i * dx) return sum * dx

在绘制了误差与分割点数量的关系图之后，我们看到梯形方法也具有第二个近似阶数，并且通常得出的结果与中点矩形方法（以下简称矩形方法）略有不同。

计算精度控制

将分裂点的数目设置为输入参数不是很实际，因为通常需要计算的积分不是给定的分区密度，而是给定的误差。如果预先知道被积物，那么我们可以预先估计误差并选择一个积分步骤，以确保达到指定的精度。但这在实践中很少是这种情况（通常，使用预先已知的功能难道不容易将积分进行预先积分吗？），因此，需要一种自动调整阶跃至给定误差的程序。

如何实现呢？估算误差的一种简单方法- 龙格规则（ Runge rule） -从n点和2 n个点计算出的积分值之差给出误差估算： $\ Delta_ {2n} \大约| I_ {2n}-I_n |$ 。与具有中心点的矩形方法相比，梯形方法更容易使分区的细度加倍。当使用梯形方法进行计算时，要使点数加倍，仅在前一个分区的各个段的中间需要函数的新值，即积分的前一个近似值可用于计算下一个。

矩形方法还有什么用？

矩形方法不需要计算段末端的函数值。这意味着它可用于在段边缘具有可积分特征的函数（例如，sin x / x或x ^-1/2从0到1）。因此，下面显示的外推方法将与矩形方法完全相同。与梯形方法的区别仅在于将步长减半时，先前计算的结果将被丢弃，但是，您可以将点数增加三倍 ，然后积分的先前值也可以用于计算新值。在这种情况下，必须将外推公式调整为不同的积分步骤比例。

从这里，我们得到带有精确控制的梯形方法的以下代码：

 def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1): """  rtol -     nseg0 -    """ nseg = nseg0 old_ans = 0.0 dx = 1.0 * (b - a) / nseg ans = 0.5 * (func(a) + func(b)) for i in range(1, nseg): ans += func(a + i * dx) ans *= dx err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) #      #       nseg *= 2 err_est = abs(ans - old_ans) return ans

使用这种方法，将不会在一个点上多次计算被积物，并且所有计算出的值都将用作最终结果。

但是在相同数量的函数计算下是否可以实现更高的精度？事实证明，在同一个网格上，存在比梯形法更精确的公式。

分段抛物线逼近

下一步是使用抛物线元素近似函数。这要求分区的段数是偶数，然后抛物线可以通过三点的点绘制，其横坐标为{{ x ₀ = a ， x ₁ ， x ₂ ），（ x ₂ ， x ₃ ， x ₄ ），...，（ x _{n -2} ， x _{n -1} ， x _n = b ）}。

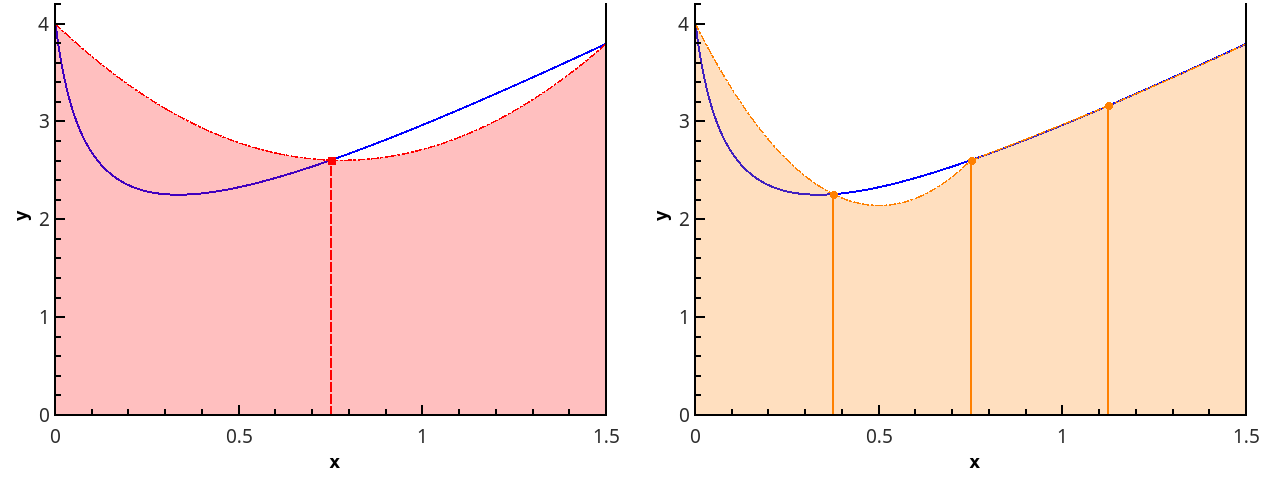
在3点和5点（ n = 2和n = 3）处的分段抛物线近似图。

在每个分段[ x _k ; x _{k +2} ]通过抛物线近似在该线段上的积分，并假设点是均匀分布的（ x _{k +1} = x _k + h ），我们获得了辛普森公式：

$I_ {Simps，n} = \ sum_ {i = 0} ^ {n / 2-1} \ frac {h} {3} [f（x_ {2i}）+ 4f（x_ {2i + 1}）+ f（x_ {2i + 2}）] = \\ = \ frac {h} {3} [f（a）+ 4f（a + h）+ 2f（a + 2h）+ ... + 4f（bh） + f（b）] ~~（4）$

公式（4）直接产生了辛普森方法的“幼稚”实现：

扰流板方向

 def simpson_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" if nseg%2 = 1: nseg += 1 dx = 1.0 * (b - a) / nseg sum = (func(a) + 4 * func(a + dx) + func(b)) for i in range(1, nseg / 2): sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx) return sum * dx / 3

要估算误差，您可以对步骤h和h / 2使用相同的积分计算方法-但这是问题所在，当使用较小的步长计算积分时，尽管新函数的一半计算将与以前相同，但必须放弃先前计算的结果。

幸运的是，如果以更巧妙的方式实现Simpson方法，则可以避免浪费机器时间。仔细观察后，我们注意到辛普森公式的积分可以通过梯形公式以不同的步长通过两个积分来表示。这在三点积分近似的基本情况中最清楚地看到 $（a，f_0），〜（a + h，f_1），〜（a + 2h，f_2）$ ：

$I_ {Simps，2} = \ frac {h} {3}（f_0 + 4f_1 + f_2）= \ frac {4} {3} h \ left（\ frac {f_0 + f_1} {2} + \ frac { f_1 + f_2} {2} \右）-\ frac {1} {3} \ cdot2h \ frac {f_0 + f_2} {2} = \\ = \ frac {4I_ {trap，2}-I_ {trap，1 }} {3}$

因此，如果我们执行将步长减少一半的过程并通过梯形方法存储最后两个计算，则具有精度控制的辛普森方法将更有效地实现。

那样的东西...

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #           nseg0 Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ ans = Quadrature.__restart(func, x0, x1, nseg0) old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = Quadrature.__double_nseg(func, x0, x1) err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0) new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans old_trapez_sum = new_trapez_sum new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans

比较梯形和抛物线法的有效性：

 >>> import math >>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 65537 4.250000001385811 >>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 2049 4.2500000000490985

如您所见，使用这两种方法都可以以相当高的精度获得答案，但是对被积数的调用次数却大不相同-高阶方法的效率高32倍！

通过绘制积分误差与步数的关系图，我们可以验证辛普森公式的近似阶为4，即数值积分误差 $| I_ {Simps，n}-I | = O（1 / n ^ 4）$ （并且使用此公式对三次多项式的积分进行计算，直至对任何偶数n > 0都舍入误差）。

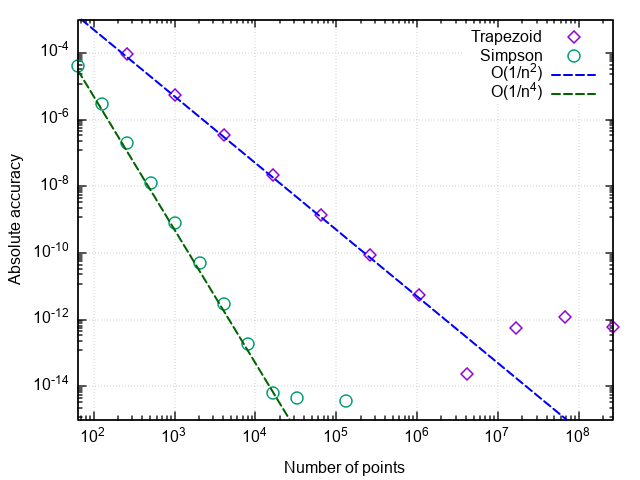
因此，与简单的梯形公式相比，效率得到了提高。

接下来是什么？

提高正交公式的精度的进一步逻辑通常是可以理解的-如果我们继续用更高程度的多项式来逼近函数，那么这些多项式的积分将越来越准确地逼近原始函数的积分。这种方法称为二次牛顿-科特公式的构造。已知多达8个近似阶的公式，但是在（2）中的加权系数_wi中出现了交替项，并且这些公式在计算中失去稳定性。

让我们尝试另一种方式。正交公式的误差表示为积分步长h的幂的级数。梯形法（和带有中点的矩形！）的一个显着特性是，为此，该系列仅包含偶数度：

$I_ {trap，n} [f，a，b] = \ int_a ^ bf（x）dx + C_2h ^ 2 + C_4h ^ 4 + C_6h ^ 6 + ...，〜h = \ frac {ba} {n } ~~~（5）$

理查森外推法是基于找到该展开的逐次逼近：不是从多项式逼近被积，而是从积分的计算出的逼近 $我（h）$ 构造了一个多项式逼近，对于h = 0，它应该为积分的真实值提供最佳逼近。

在分区步长的偶数幂中扩展积分误差会极大地加速外推的收敛，因为对于2 n阶近似，梯形方法只需要n个积分值。

如果我们假设每个后续项都小于前一个项，那么我们可以顺序排除h的度数，而h的度数具有使用不同步长计算的积分近似值。由于上述实现很容易使我们将分区分成两半，因此考虑步骤h和h / 2的公式很方便。

$I_ {trap，n}-I \约C_2h ^ 2;〜I_ {trap，2n}-I \约C_2 \左（\ frac {h} {2} \右）^ 2$

可以很容易地看出，梯形公式的误差的高级项将完全给出辛普森公式：

$I = I_ {trap，2n}-C_2 \左（\ frac {h} {2} \ right）^ 2 + O（h ^ 4）\大约I_ {trap，2n}-\ frac {I_ {trap， 2n} -I_ {trap，n}} {1-2 ^ 2} = I_ {Simps，2n}$

对Simpson公式重复类似的过程，我们得到：

$I_ {Simps，2n}-I \大约C_4 \左（\ frac {h} {2} \右）^ 4;〜I_ {Simps，n}-I \大约C_4h ^ 4$

$I = I_ {Simps，2n}-C_4 \左（\ frac {h} {2} \ right）^ 4 + O（h ^ 6）\约I_ {Simps，2n}-\ frac {I_ {Simps， 2n} -I_ {Simps，n}} {1-2 ^ 4}$

如果继续，将显示以下表格：

2订单	4订单	6阶
我 _0,0
我 _1,0	我 _1,1
我 _2.0	我 _2.1	我 _2.2
...	...	...

第一列包含通过梯形法计算的积分。从顶行向下移动时，线段的划分变小两倍，而从左列向右移动时，积分的逼近顺序增加（即第二列包含通过Simpson方法计算的积分等）。

可以从扩展（5）推断出的表元素与递归关系相关：

$I_ {i，j} = I_ {i，j-1}-\ frac {I_ {i，j-1} -I_ {i-1，j-1}} {1- \左（\ frac {h_ {ij}} {h_i} \ right）^ 2} = I_ {i，j-1}-\ frac {I_ {i，j-1} -I_ {i-1，j-1}} {1-2 ^ {2j}} ~~~（6）$

可以从一行中不同阶的公式之差来估计积分近似值的误差，即

$\ Delta_ {i，j} \大约I_ {i，j}-I_ {i，j-1}$

使用Richardson外推法和梯形积分法称为Romberg方法。如果Simpson方法考虑了梯形方法的两个先前值，则Romberg方法将使用之前由梯形方法计算的所有值来获得更精确的积分估计。

实作

在Quadrature类中添加了一个附加方法

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #          nseg0  Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True): """   nseg0 -     maxcol -   """ #   Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]] i = 0 maxcol = max(0, maxcol) ans = Itable[i][i] error_est = max(1, abs(ans)) while (error_est > abs(rtol * ans)): old_ans = ans i += 1 d = 4.0 ans_col = min(i, maxcol) Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1)) for j in range(0, ans_col): diff = Itable[i][j] - Itable[i - 1][j] Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0) d *= 4.0 ans = Itable[i][ans_col] if (maxcol <= 1): #       error_est = abs(ans - Itable[i - 1][-1]) elif (i > maxcol): error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)]) else: error_est = abs(ans - Itable[i - 1][i - 1]) print("Total function calls: " + str(Quadrature.__ncalls)) return ans

让我们检查一下高阶近似的工作原理：

 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) #  Total function calls: 65537 4.250000001385811 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) #  Total function calls: 2049 4.2500000000490985 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4) Total function calls: 257 4.250000001644076

我们相信，与抛物线方法相比，对被积物的调用次数又减少了8倍。随着所需精度的进一步提高，Romberg方法的优势变得更加明显：

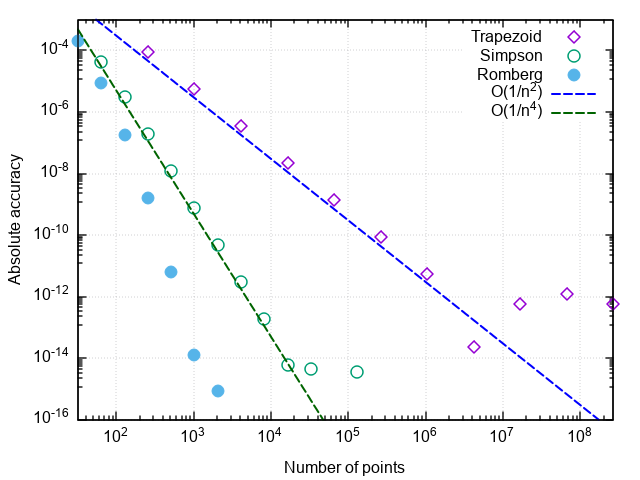
一些注意事项

备注1.这些问题中的函数调用次数表示计算积分时的和数。减少被积数的计算数量不仅节省了计算资源（尽管对于更优化的实现也是这种情况），而且还减少了舍入误差对结果的影响。因此，当您尝试计算测试函数的积分时，当您尝试达到5×10 ^-15的相对精度时，梯形方法会冻结，抛物线方法-所需的精度为2×10 ^-16 （这是双精度数字的极限），而Romberg方法可以应付计算测试积分直至机器精度（低误码率）。即，不仅对于给定数量的函数调用，积分的精度提高了，而且积分计算的最大可达到的精度也得到了提高。

备注2.如果在指定某个精度时该方法收敛，则并不意味着积分的计算值具有相同的精度。首先，这适用于指定误差接近机器精度的情况。

备注3.尽管针对多个函数的Romberg方法以几乎不可思议的方式工作，但它假定被积物对高阶导数有界。这意味着对于具有扭结或断裂的函数，它可能比简单方法更糟糕。例如，积分f （ x ）= | x |：

 >>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5) Total function calls: 9 5.0 >>> Quadrature.simpson(abs, -1, 3, rtol=1e-5) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3) Total function calls: 33 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4) Total function calls: 33 5.000001383269357

备注4.似乎逼近阶数越高越好。实际上，最好将Romberg表中的列数限制为4-6。要理解这一点，请看公式（6）。第二项是第j -1列的两个连续元素之差除以约4 ^j 。因为第j列包含2 j阶积分的近似值，则差本身约为（1 / n _i ） ^{2 j〜4} ^{- ij} 。考虑到除法，获得〜4- ^{（ i +1） j〜4} ^{- j ²} 。即对于j〜7 ，（6）中的第二项在添加浮点数时降低阶数后会失去准确性，并且近似阶数的增加会导致舍入误差的累积。

备注5.利益相关方可以出于利益考虑使用所描述的方法来找到积分。 $\ int_0 ^ 1 \ sqrt {x} \ sin {x} dx$ 相当于他 $\ int_0 ^ 1 2t ^ 2 \ sin {t ^ 2} dt$ 。正如他们所说，感受不同。

结论

介绍了统一网格上函数数值积分的基本方法的描述和实现。演示了如何通过简单的修改，在梯形法的基础上使用Romberg方法获得正交公式的类，从而显着加快了数值积分的收敛速度。该方法很好地用于集成“普通”功能，即在积分间隔上变化不大，在段的边缘没有奇点（见注5），快速振荡等。

( [3] — C++).

文学作品

A.A. , .. . . .: . 1989.
J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
WH Press, SA Teukolsky, WT Vetterling, BP Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.

定积分的计算：基本算法