对于涟漪，有趣的人和电感的问题

法律14（爱迪生定律）“更好”是“好”的敌人

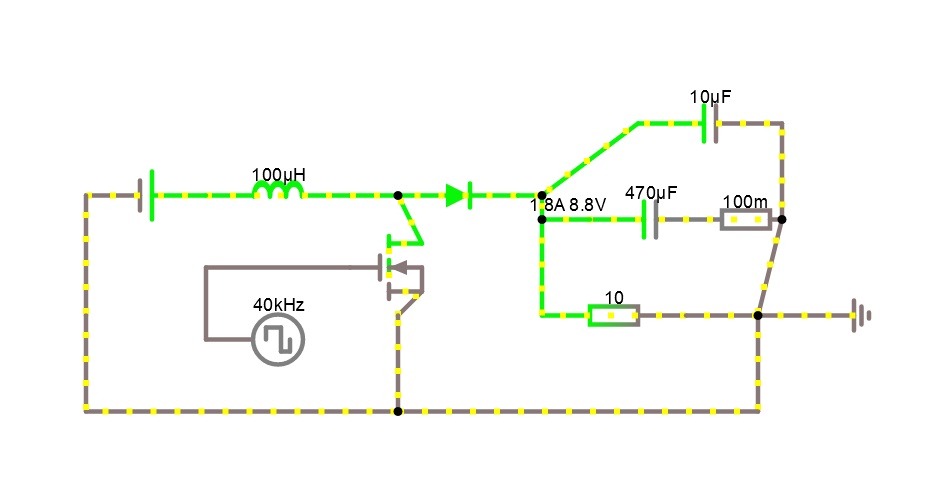
最近，我在同事中反复提到的同事（通常，作为沃森博士的转世，主要目的是使主角更加辉煌，我有个类似的笑话，丹尼尔）决定精通电源设计（用于低功率的开始，就会看到它）。 由于这种情况发生在201年代，晶体管既便宜又小（甚至带有驱动器），电感又大又贵（很好，不像以前那么大，但是仍然不小），因此在微控制器中装有升压非反相（桥）电路。控制元素的作用。 该方案涉及许多有趣的问题，其中一些问题在ST4 Ann448中得到了回答（不是全部，而且还不完整，也许我会写更多有关此的内容），但这有些不同。

组装完电路后，一位同事编写了一系列测试，从而可以检查电路的正确性（发现并纠正了错误）和单个元件的功能（也发现并修复了错误）。 （我不明白，达尼尔，你为什么不自己写，特别是关于输出键助推器-这很有启发性）。 其中一项测试是将设备用作具有固定占空比的升压电源，该功能通常得到确认，输出电压根据计算模型而变化。 好吧，总之，我们决定查看源输出处的纹波电压。 测试模式的等效电路显示在KDPV上。

在这里我们遇到了一个有点难以理解的现象-输出波形与通过脉动幅度计算出的波形有很大的不同（嗯，这是普遍预期的，因为实际成分的参数将始终与规范中指示的参数有所不同，但有时不会如此），并且波形（但这是完全无法理解的）。 具体波形如图1所示（绿色），在其上标出了预期的波纹形状（红色），在我看来，差异是显而易见的。 最重要的是，令人惊讶的是电容器不断放电（突变区域除外），这与理论上预测的稳定状态下一段时间内流经电容器的平均电流等于零的情况形成了鲜明的对比，稳态是整个转换器计算方法的基础。



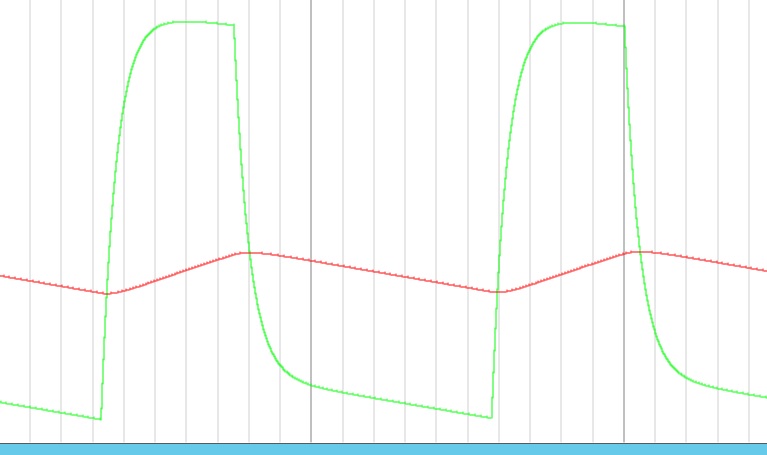
我们开始推理。 巨大的ESR电容器可以完美地解释电压的急剧上升，我们甚至可以估算出其值= dU / I / 2，这使我们达到了100 mOhm-当然有点太大，但是很有可能。 但是，为什么在电感的功率传输周期中，我们没有看到电容两端的电压出现特征性上升？ 需要进行额外的研究，为此，有必要在另一个设备上重现缺陷。 由于无法收集第二块板（更确切地说，没有愿望，这是决定因素），因此您需要虚拟电路，而Google“电子电路模拟器”会导致一个完全吸引人的网站falstad.com。 （需要注意的是-作者了解许多其他模拟器的存在，并且他使用了很多次，但是IT部门的安全策略使其无法安装该软件包，甚至破获的软件包也是如此，所以在线就是我们的一切。）

我找到了一个建模程序，阅读了它的创建历史，并且我知道这是一个独立的项目，也就是说，一个人（在业余时间）编写了一个模拟器（使用Java），为它提供了一组模型并通过该应用程序支持站点的工作-疯了。 我了解模拟电子电路的基本原理，我可以承认许多模型都可以在Web上以可访问的形式访问，但是，尽管如此，我也没有编写这样的模拟器（以及绝大多数哈布拉赫居民）。 但是压制嫉妒的感觉，并开始研究有问题的方案。

我不是立即制作电路模型，而是（使用视频课），我正在学习以波形图的形式可视化结果（该程序使我们能够以微型圆圈的形式监视正在研究的电路中的电流，这很有趣，但很有启发性，但信息不多，尽管您可以展示电子的运动，然后圆圈将沿相反的方向运行，这虽然更有趣，但没有更多信息），并观察结果。 结果的接收与理论上的预测完全吻合，这并不奇怪-我们拥有与计算中一样完美的所有元素。


我加上了电阻的期望值，很惊讶地看到脉动的形状发生了戏剧性的变化，并且与实验中观察到的完全吻合，这让我们感到高兴，这意味着我们可以继续研究该模型。 首先，我测量电容器两端的电压，并高兴地确保伏秒平衡不被破坏，并且电容器在工作周期中应充电和放电。 然后，负载上电压的行为就变得清晰了-这是电容器两端的电压与电阻两端的压降之和，该压降与流动的电流成比例。 由于在能量从电感传递到电容的过程中，流经电感的电流会发生变化（减小），因此会导致电阻下降的减小，并且从电阻的某个值开始，电容上与电荷相关联的电压上升将获胜。

为了检验我们的假设，让我们玩一下电路的参数（我强烈建议您在提供的页面上自己做），首先我们关闭陶瓷电容器，这将以1ms的时间常数消除前沿的平滑，并让我们以纯净的形式观察效果。 我们开始增加电阻，我们看到了特征阶梯的出现，该阶梯开始增大。 从某个角度，您可以看到充电部分中负载处的正向电压的倾斜角度开始减小，直到该部分变为水平，然后变为下降的部分。

我们进行了最后一个实验，该实验表明除了电感中的电流下降之外，电压下降没有其他原因（无论如何我们都看不到它们，但您永远不会知道...）-有必要减小电感中的电流纹波，并且最简单的方法是通过增大电感来实现。 在现实生活中，要获得一个电流为4A的1 mF线圈的任务并不容易，但是在仿真器中再简单不过了-可以肯定的是，电流纹波急剧减小，并且输出电压又具有线性增大的截面。 与往常一样，没有任何奇迹发生，并且该计划中发生的所有过程都有自然科学的解释，即BST。

我们返回原始带电电路，查看日期的电容参数，查看预期的100mOhm电阻，问一个困惑的问题“为什么在这里”，我们得到的答案是“根据计算，花了200uf，我决定放更多”（“这让Victor Stepanovich回忆起是王先生的远见卓识的人-对不起，不是我的话，我们在桌子上放了两块100微米的陶瓷（毫米尺寸的100微米的陶瓷），卡尔-如果我在20年前被告知，我会在寺庙上转动手指，现在......组分b 因为他们做了多年来一个巨大的飞跃，虽然电路设计不能说，一切都被认为是向我们），一切都刚刚好。 这使我想起另一个同样引人注目的短语：“没有必要，因为它更好，但也有必要，应该如此。”

最后，我要感谢法尔斯塔德先生，他很高兴利用他的精彩计划，并为这样的人还在做而感到高兴，否则我离开罗伯特·皮斯后会感到无聊。 尽管我并不完全无聊-大约3年前，我发现了一个了不起的程序和一个模拟器-VMLab，并且处于免费软件的状态-这个概念中可能有些东西，因为如此出色的人正在推广它。 您还可以回想起哥斯达黎加（Godbolt）-它也非常好，也许都是一样，并不是一切都消失了，“他们不再做这样的人”这句话是错的，他们做的只是做一些不同的事情。

PS。 既然我们在谈论电感（是的，尽管不是很久，我们还是在谈论它们），所以我想谈谈与从标准产品中选择电感有关的功能（我想说更苛刻，但在哈伯瑞不欢迎“有毒行为”）。 主要参数以及电感本身是通过线圈的允许电流，此处存在令人讨厌的细微差别，我们将对此进行考虑。

首先，让我们通过以下事实来确定超过最大电流（饱和电流）的危险，正如您可能猜到的那样，电感进入饱和模式，在该模式下，流动电流与磁芯磁化强度之间没有线性关系，这会由于磁化强度反转而导致能量损失。 此参数具有2个应考虑的功能：

1.实际上，对于每个实际电感，此参数均为零，因为对于任何流动的电流，都会发生非线性，并且问题仅在于特定点的非线性程度。 在我青年时期，通常给出一个电流值为损耗为5％的值（这是正确的方法），以便您可以确定在较低电流下的电感。 不幸的是，现在有些制造商指出电流损失为20％，另一些制造商指出电流损失为30％，因此，在接近指示电流的情况下，您将对效率方面的结果感到困惑。 当然，在日期上会诚实地表明边界电流的损耗水平，您可以随时回答RTFM（F），但是就开发人员的期望而言，以某种方式有些不诚实。 我了解到，营销部门坚持要在传单中提供最高的费用（诚实的当前水平将减少50％），但是我仍然主要还是工程师。

2.这不是平均电流，而是最大电流，并且如果饱和电流短期过剩（这对于开关电源来说是典型的），那么即使平均电流要小得多，损耗也是不可避免的。 此功能应该是可以理解的，在这里制造商很诚实-您必须自己考虑。 因此，需要保持连续模式，因为在这种模式下，最大电流与平均值之比最小，并且为一比二。

但是还有一个以前根本不存在的参数。 事实是，在过去的10多年中，从磁芯的角度来看，出现了许多具有令人称奇的参数的出色材料，主要是磁导率和频率特性。 所有这些使得有可能将绕组元件的几何尺寸减小一个数量级（或什至不减小一个），同时增加工作频率。 但是您必须为此付出一切代价-如果您可以将铁心铁心的变压器加热到铜线的熔点（很容易发生短路），并且效率没有损失（可能已经损失了，但并不引人注目） ，这种技巧不适用于现代材料，当加热到一定温度以上时，导磁率（以及饱和电流）开始下降，其后果可完全预测。

因此，由于上述原因，第二个参数是通过绕组的最大允许平均电流。 通常，它比饱和电流小2倍（尽管这不是必需的），因此，如果您处于连续性模式的边界，那么一切都很好，并且满足所有条件（不要忘了损耗的20％至30％），但是如果您的内心深处连续性和最大电流区域=平均值的120％，并且没有超过饱和电流，那么您仍然需要检查平均电流的允许性。 因此，根据经验法则-将现代线圈的饱和电流除以约1.5（更多的电流已经太多）并选择此标准，您将在开发的电路中感到满意和高效。

顺便说一句，好中国人就是这样做的-他们将一个饱和电流为12A的电感放到一个8A的电流源中，一切效率都达到了90％。