在印度，我们的INN有一个本地类似物-“ adhar”。 电子系统“ eAdhar”固定在其上。 在eAdhara中，每个字母都用密码阻止。 一切都会好起来的，但是密码是根据一个简单的模式组成的：名称的前四个字母是大写字母和出生年份。
四个大写字母和四个数字。 其中，可以编辑2,821,109,909,456个组合。 如果您每秒检查一千个组合，则一个密码将花费90年。
太久了 我们可以加速几十亿倍吗？
92年→52天。 组别
通过3万亿个组合，我们还有更多。 不过，模板是已知的：
([AZ][AZ][AZ][AZ]) ([0–9][0–9][0–9][0–9]) (4 ) (4 ) ( 1) ( 2)
在这种模式下，可以立即丢弃S2N65GE1行。 您会得到多少组合？
第一组是四个字母字符。 26个选项，4个职位，我们得到：
10位数字的4个位置，类似地：
从中我们获得组合的总数：
让我们估计一下现在的蛮力速度要快多少。 同样，我们从每秒1000次尝试开始：
或52天21小时22分40秒。 而不是92年。 还不错 但是仍然很长一段时间。 还有什么可以做的？ 同一件事-减少组合数量。
52天→12小时。 打开常识
第一组和第二组不是随机字符集，而是名称和出生年份的首字母。 让我们从出生年份开始。
为出生于1642年或2594年的用户选择密码是没有意义的。 因此，组合范围可以安全地从0000–9999减少到1918–2018。 因此，我们将涵盖0至100岁所有生命的正负。 因此，分别减少了组合数量和时间：
或12小时41分37秒。
12小时→2分钟。 我们牺牲准确性
12小时很棒，但是... 我们需要更深入地研究 。
现在，我们拥有4,500万种组合，可以准确地覆盖所有eAdhara用户。 但是如果为了提高速度而牺牲一小部分怎么办？
我们完善了数字组合。 信件做类似的事情。 逻辑很简单：没有出生年份9999，并且以同样的方式，也没有以“ AAAA”开头的印度名字。 但是如何确定所有合适的组合？
我从目录网站收集了印度名字， Photon在这方面给了我很大帮助。 结果是3,283个唯一名称。 仍然需要修剪前四个字母并删除重复的字母：
grep -oP ”^\w{4}” custom.txt | sort | uniq | dd conv=ucase
原来有1,598个前缀！ 有很多重复项，因为名称中的“ Sanjeev”和“ Sanjit”之类的前四个字母是相同的。
1,598个前缀-不足以容纳十五亿人口吗？ 我同意 但是请不要忘记这些是前缀，而不是名称。 我将结果列表发布在Gist上 。 实际上，应该有更多。 您可能会感到困惑，从其他站点收集10,000个名称并获得3,000个唯一的前缀，但是我没有时间这样做。 因此，我们将从1,598开始。
让我们计算一下现在需要多少时间：
或2分39.8秒。
2分钟→2秒。 维基百科来营救
2分40秒是对所有组合进行分类所需的时间。 但是，如果第十一组合是正确的怎么办？ 还是最后一个？ 还是第一个？
现在，组合列表按字母顺序排序。 但这毫无意义-谁说“ A”上的名字比“ B”上的名字更普遍，或者说一岁的孩子多于七十岁的孩子？
有必要考虑每种组合的可能性。 他们在Wikipedia上写道：
在印度，超过50％的人口年龄在25岁以下，超过65％的人口在35岁以下。
基于此，您可以尝试以下方法，而不是列表1–100：
25–01 ( , , ) 25–35 36–100
然后事实证明，第一个概率 
组合增加到50％。 我们破解了一半的密码 秒！ 在下面 秒，我们将再获取15％的密码。 总计-55.9秒内输入密码的65％。
现在到名字了。
在Google中，很容易找到任何国家的TOP-100名称。 根据印度的数据，我将适当的组合移至列表的顶部。 我们假设印度有15％的人口享有流行的名字。 因此，几乎可以立即破解15％的密码。
印度教徒-印度人口的80％。 因此，如果您将印度教徒的名字放在列表中的上方，它将加速80％的尝试。 在上一步之后，我们离开了 尝试。 如果其中80％是印度教徒的名字，那么79％（我们将1％留给流行，但不是印度教徒的名字），我们将在接下来的65％的尝试中努力。
让我们将年龄统计信息一起计算在内。 分为几组：
100: { 50: 00 25 { 7: , 43: { 34: , 9: } } 15: 26 35 { 3: , 13*: { 10: , 3: } } 45: 36 100 { 7: , 38: { 30: , 8: } } }
现在，让我们制定一个有效的密码破解算法：
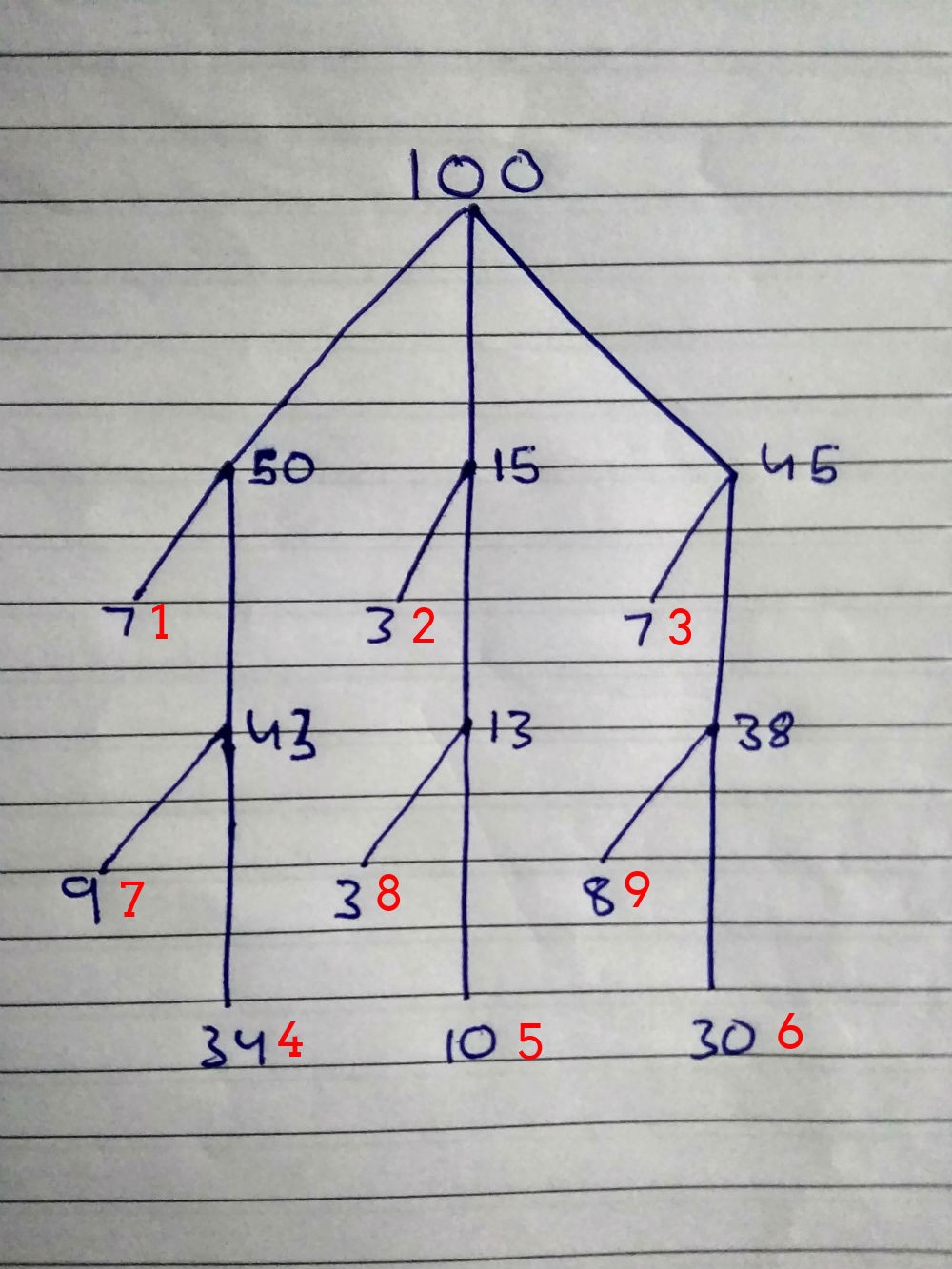
红色数字是搜索的优先级。 首先测试第一类人的组合，然后测试第二个，然后测试第三个，依此类推。
现在入侵需要多少时间？
第一阶段
1 = 11秒破解7个密码
2 = 3秒破解3个密码
3 = 11秒破解7个密码
我们破解了17个人的密码，仍然保留了83个人，我们将从列表中删除以前的组合，并尝试以下设置-4，5，6。
第二阶段
4 = 54秒破解34个密码
5 = 16秒破解10个密码
6 = 47秒破解30个密码
同样，删除先前阶段的组合。
第三阶段
7 = 14秒破解9个密码
8 = 5秒破解3个密码
9 = 12秒破解8个密码
总时间 ： 秒或2分13秒。
密码破解 ：100
一个密码的平均时间 ： 秒。
92年→1.73秒。 尼采这样吧？