打开您的咖啡馆，您想知道以下问题的答案：“最靠近此点的另一个咖啡馆在哪里？” 这些信息将帮助您更好地了解您的竞争对手。
这是“
最邻近 ”搜索问题的一个示例，该问题已在计算机科学中被广泛研究。 给定一组信息和一个新点，您需要找到与现有点最接近的一点？ 在基因组研究，图像搜索和Spotify建议等领域的许多日常情况下都会出现这样的问题。
但是，与咖啡馆示例不同，有关最近邻居的问题通常非常复杂。 在过去的几十年中，计算机科学家中最伟大的头脑开始寻找解决此问题的最佳方法。 尤其是，他们试图应对因在不同数据集中对点之间的“接近度”定义非常不同而引起的复杂性。
现在，一组计算机科学家提出了一种全新的方法来解决寻找最接近的邻居的问题。 在一
对 论文中，五位科学家详细描述了第一种通用方法，用于解决为复杂数据寻找最接近的邻居的问题。
麻省理工学院的IT专家
Peter Indik说：“这是使用单一算法技术涵盖广泛空间的第一个结果。”
距离差
我们非常依赖确定距离的唯一方法，因此很容易忽略其他方法的可能性。 通常，我们以欧几里得距离来衡量距离-两点之间的直线。 但是，在某些情况下，其他定义更有意义。 例如，
曼哈顿的距离可使您转90度，就像沿着矩形道路网移动一样。 要测量一条直线上可能为5公里的距离，您可能需要在一个方向上越过城市3公里，然后在另一个方向上越过4公里。
也有可能不在地理意义上谈论距离。 一个社交网络中的两个人，两个电影或两个基因组之间的距离是多少？ 在这些示例中，距离表示相似度。
有数十种距离度量标准，每个距离度量标准都适合特定任务。 以两个基因组为例。 生物学家使用“
Levenshtein距离 ”或编辑距离对其进行比较。 两个基因组序列之间的编辑距离是将其中一个变成另一个所需的添加，缺失，插入和取代的数量。
编辑距离和欧几里得距离是距离的两个不同概念，因此不可能将两者相减。 这种不兼容性存在于许多对距离度量标准中，并且对于试图开发用于查找最近邻居的算法的计算机科学家构成了障碍。 这意味着适用于一种距离类型的算法将不适用于另一种距离类型-更确切地说，直到现在，直到出现一种新的搜索类型为止，它都是如此。
亚历山大·安多尼圆平方
查找最接近邻居的标准方法是将现有数据划分为子组。 例如，如果您的数据描述了牧场中母牛的位置，则可以将它们围成一个圈。 然后，我们将一头新牛放到草地上，然后问一个问题：它属于哪个圆圈？ 实际上可以保证新母牛的最近邻居将在同一圆圈内。
然后重复该过程。 将圆划分为子圆，进一步将这些单元划分，依此类推。 结果，有一个只有两个点的单元：现有点和新点。 该现有点将是您最近的邻居。
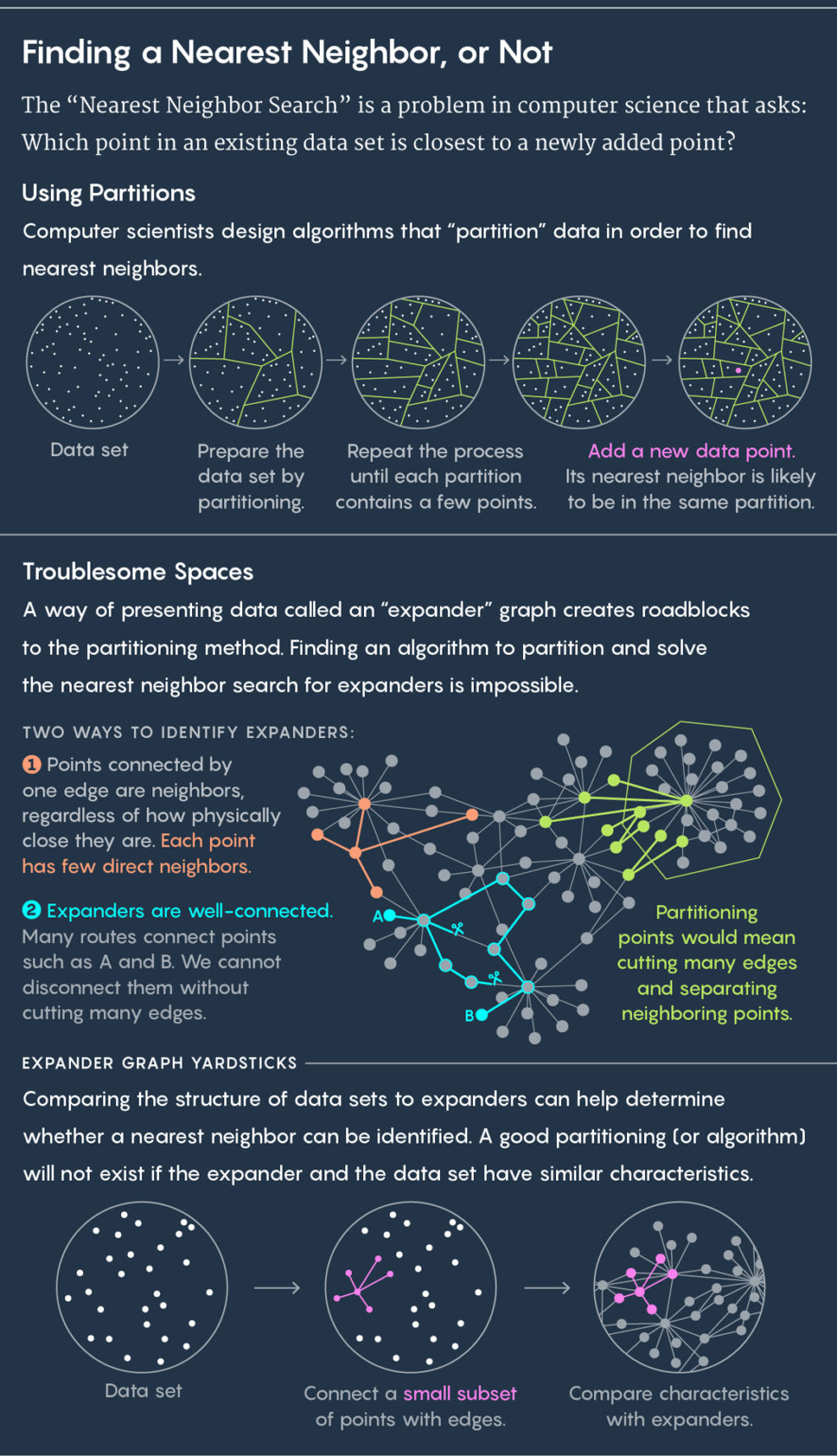以上是将数据划分为单元格。 下面是扩展图的用法。算法会绘制单元格，好的算法会快速且良好地绘制它们-也就是说，在这种情况下，不会出现新母牛掉入一个圆圈且其最接近的邻居陷入另一个圆圈的情况。 微软研究院计算机科学专家
Ilya Razenshtein说：“我们希望这些单元中的近点更多地出现在彼此相同的驱动器中，而远处的罕见点是罕见的。” ，普林斯顿大学的
Assaf Naor ，多伦多大学的
Alexander Nikolov和哥伦比亚大学的
Eric Weingarten 。
多年来，计算机科学家提出了各种算法来绘制此类单元格。 对于小数据（例如，一个点由少量值确定的地方，例如奶牛在牧场中的位置），算法会创建所谓的 “
Voronoi图 ”可准确回答有关最近邻居的问题。
对于多维数据，其中一个点可以由数百或数千个值确定，因此Voronoi图需要太多的计算能力。 取而代之的是，程序员使用“
局部敏感哈希 ”绘制单元格
， Indik和Rajiv Motwani于1998年首次
描述了这种方法。LF算法随机绘制单元格。 因此，它们的工作速度更快，但准确性较差-它们会确保与实际的最近邻居的距离不超过给定距离，而不是找到确切的最近邻居。 可以想象这是Netflix的电影推荐，虽然不完美，但足够好。
自1990年代后期以来，计算机科学家提出了LF算法，该算法为给定距离度量值找到最近邻居的任务提供了近似解决方案。 该算法非常专业，针对一种距离度量开发的算法无法用于另一种。
“在某些特定情况下，您可以针对欧氏距离或曼哈顿距离提出一种非常有效的算法。 但是我们没有适用于大距离距离的算法，” Indik说。
由于使用一种度量标准的算法无法用于另一种度量标准，因此程序员提出了一种变通方法。 通过一个称为“嵌入”的过程，他们将度量标准强加给他们没有好的算法的度量。 但是，指标的对应关系通常不准确-有点像圆孔中的方钉。 在某些情况下，嵌入根本不起作用。 有必要提出一种通用的方法来回答有关最近邻居的问题。
伊利亚·拉岑施泰因（Ilya Razenshtein）意外结果
在一项新工作中，科学家放弃了对特殊算法的搜索。 取而代之的是，他们问了一个更广泛的问题：是什么阻碍了在特定距离度量标准上开发算法？
他们认为，应归咎于与扩展图或
expander相关的令人不快的情况。 扩展器是一种特殊的图形，一组点通过边连接。 图具有自己的距离度量。 图的两点之间的距离是从一个点到另一点所需的最小线数。 您可以想象一个图，它表示社交网络中人与人之间的联系，然后人与人之间的距离等于将他们分隔开的联系数。 例如，如果朱利安·摩尔有一个朋友，而凯文·培根是他的朋友，那么从摩尔到培根的距离是3。
扩展器是一种特殊类型的图，乍一看具有两个冲突的属性。 它具有很高的连通性，也就是说，如果不切开多个边缘就不能断开两个点。 同时，大多数点都与很少的其他点相连。 因此，大多数点之间相距甚远。
这些属性的独特组合-良好的连通性和少量边缘-导致以下事实：在扩展器上，无法快速搜索最近的邻居。 将其划分为单元格的任何尝试都将分隔彼此靠近的点。
这项工作的合著者Weingarten说：“将扩张器切成两部分的任何方法都需要切掉多个肋，这会分割许多紧密间隔的顶点。”
到2016年夏天，Andoni，Nyokolov，Rasenstein和Vanguarten知道，对于扩展器，无法找到找到最接近邻居的好算法。 但是他们想证明，在寻找计算机科学家陷入困境的良好算法时，无法针对其他许多距离度量（即度量）构造此类算法。
为了找到此类算法不可能的证据，他们需要找到一种将扩展器指标嵌入其他距离指标的方法。 使用这种方法，他们可以确定其他指标具有与扩展器属性相似的属性，从而阻止了他们制定好的算法。
埃里克·温加顿四位计算机科学家去了普林斯顿大学的数学家阿萨夫·瑙鲁（Assaf Naoru），他的先前工作非常适合扩展器这一主题。 他们要求他帮助证明扩展器可以嵌入各种类型的指标中。 Naor很快就回了一个答案-但不是他们所期望的。
安多尼说：“我们请阿萨夫（Assaf）帮助我们发表这一声明，他证明了相反的说法。”
Naor证明扩展器不适合称为“
标准空间 ”（也包括诸如欧几里得空间和曼哈顿空间之类的度量）的一类距离度量。 根据Naor的证据，科学家遵循以下逻辑链条：如果扩展器不适合距离度量，则应该有一种很好的方法将其分解为细胞（因为正如他们所证明的那样，扩展器的属性是对此的唯一障碍）。 因此，即使没有人找到，也必须有一个好的算法来找到最近的邻居。
五名研究人员在一份于11月完成并于4月上传的
论文中发表了他们的发现。 接下来是第二份工作，他们于今年完成并于8月
出版 。 在其中，他们使用在编写第一篇著作时获得的信息来找到一种快速算法，该算法可以找到规范空间的最近邻居。
Weingarten说：“第一项工作表明存在一种将度量标准分为两部分的方法，但是没有快速完成该方法的方法。” “在第二项工作中，我们认为存在一种分离点的方法，此外，这种分离可以使用快速算法来完成。”
结果，新作品首次在多维数据中概括了对最近邻居的搜索。 程序员不必为特定的指标开发专门的算法，而是采用通用的方法来查找算法。
Weingarten说：“这是一种开发算法的有序方法，可以在您需要的任何距离度量标准中找到最近的邻居。”