我很想将文章命名为“可怕的STL算法效率低下”之类的诱惑-您知道,这只是为了培训如何创建醒目的标题的艺术。 但是,尽管如此,他还是决定保持礼节的范围内-最好是让读者对文章的内容发表评论,而不是愤世嫉俗。
在这一点上,我将假定您了解一些C ++和STL,并且还要注意代码中使用的算法,它们的复杂性以及与任务的相关性。
演算法
您可以从现代C ++开发人员社区中听到的众所周知的技巧之一不是骑自行车,而是使用标准库中的算法。 这是个好建议。 这些算法安全,快速,经过多年测试。 我还经常提供有关应用它们的建议。
每次您要为其编写另一个文件时-您都应该首先记住STL(或boost)中是否已经有一行东西可以解决此问题。 如果有的话,通常最好使用它。 但是,在这种情况下,我们还应该了解标准函数调用背后的算法是什么,其特点和局限性。
通常,如果我们的问题与STL中算法的描述完全匹配,那么最好将其应用并“先行”应用。 唯一的麻烦是,数据并非总是以标准库中实现的算法希望接收的形式存储。 然后,我们可能会想到先转换数据,然后仍然应用相同的算法。 好吧,你知道,就像那个数学笑话“把水壶里的火扑灭。 任务减少到上一个。”
套路口
想象一下,我们正在尝试为C ++程序员编写一个工具,该工具将捕获所有默认变量([=]和[&]),从而找到代码中的所有lambda,并显示提示,以将其转换为具有捕获变量的特定列表的lambda。 像这样:
std::partition(begin(elements), end(elements), [=] (auto element) {
在使用代码解析文件的过程中,我们将必须将变量的集合存储在当前范围和周围范围的某个位置,如果检测到lambda并捕获了所有变量,则将这两个集合进行比较并提供转换建议。
一组在父范围内带有变量,另一组在lambda内带有变量。 要形成建议,开发人员只需找到他们的交集。 当STL中的算法描述非常适合该任务时就是这种情况:
std :: set_intersection接受两个集合并返回它们的交集。 该算法简单易行。 它需要两个排序的集合,并并行运行它们:
- 如果第一个集合中的当前项目与第二个集合中的当前项目相同-将其添加到结果中,然后移至两个集合中的下一个项目
- 如果第一个集合中的当前项目小于第二个集合中的当前项目,请转到第一个集合中的下一个项目
- 如果第一个集合中的当前项目大于第二个集合中的当前项目,请转到第二个集合中的下一个项目
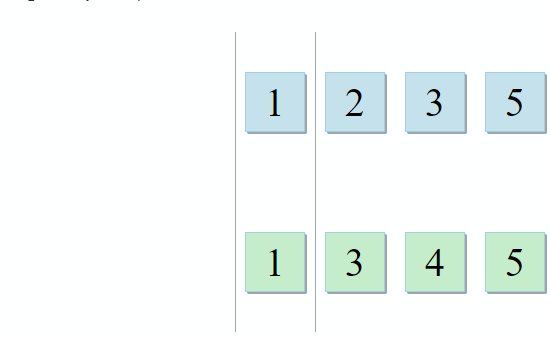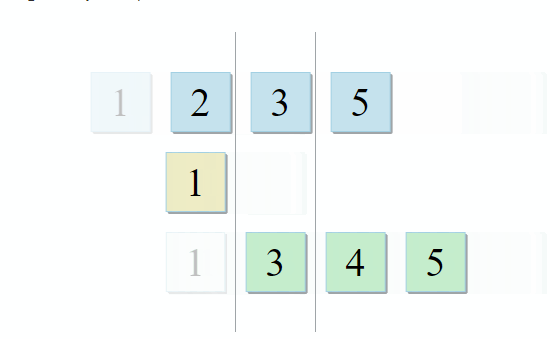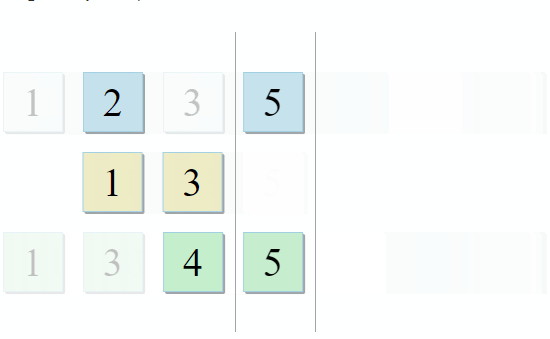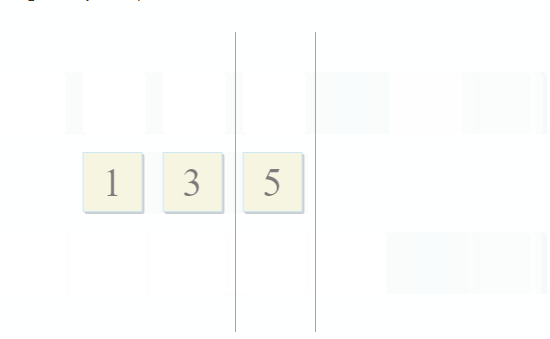
在算法的每一步中,我们都沿着第一个,第二个或两个集合移动,这意味着该算法的复杂度将是线性的-O(m + n),其中n和m是集合的大小。
简单有效。 但这只是到目前为止,对输入集合进行了排序。
排序
问题在于,通常不对集合进行排序。 在我们的特定情况下,将变量存储在某种类似于堆栈的数据结构中很方便,在进入嵌套作用域时将变量添加到下一个堆栈级别,而在离开该作用域时将其从堆栈中删除。
这意味着变量将不会按名称排序,并且我们不能直接在其集合上使用std :: set_intersection。 由于std :: set_intersection需要在输入处进行完全排序的集合,因此可能会出现这种想法(我在实际项目中经常看到这种方法),然后在调用库函数之前对集合进行排序。
在这种情况下进行排序将杀死使用堆栈根据变量范围存储变量的整个想法,但这仍然是可能的:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_1(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { std::sort(first1, last1); std::sort(first2, last2); return std::set_intersection(first1, last1, first2, last2, dest); }
结果算法的复杂度是多少? 像O(n log n + m log m + n + m)之类的东西是准线性复杂度。
排序少
我们可以不使用排序吗? 我们可以,为什么不呢。 我们将只在第二个线性搜索中从第一个集合中搜索每个元素。 我们得到复杂度O(n * m)。 我也经常在实际项目中看到这种方法。
除了可以选择“不对所有内容排序”和“不对任何内容进行排序”之外,我们可以尝试找到Zen并进行第三种选择-仅对其中一个集合进行排序。 如果其中一个集合已排序,而第二个集合未排序,那么我们可以一次遍历一个未排序集合的元素,然后在排序后的二进制搜索中进行搜索。
该算法的复杂度为O(n log n),用于对第一个集合进行排序; O(m log n),用于搜索和检查。 总的来说,我们获得了复杂度O((n + m)log n)。
如果决定对另一个集合进行排序,则得到复杂度O((n + m)log m)。 如您所知,在此处对较小的集合进行排序以获得最终复杂度O((m + n)log(min(m,n))是合乎逻辑的
该实现将如下所示:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_2(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_2(first2, last2, first1, last1, dest); return; } std::sort(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return std::binary_search(first1, last1, FWD(value)); }); }
在我们的具有lambda函数和捕获变量的示例中,我们将排序的集合通常是lambda函数的代码中使用的变量的集合,因为与周围的lambda范围相比,变量可能更少。
散列
本文讨论的最后一个选项是将散列用于较小的集合,而不是对其进行排序。 这将使我们有机会在其中搜索O(1),尽管散列的构建当然会花费一些时间(从O(n)到O(n * n),这可能会成为问题):
template <typename InputIt1, typename InputIt2, typename OutputIt> void unordered_intersection_3(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_3(first2, last2, first1, last1, dest); return; } std::unordered_set<int> test_set(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return test_set.count(FWD(value)); }); }
当我们的任务是一致地比较一些小集合A与一组其他(大)集合B 1,B 2,B ...时,散列方法将是绝对的赢家。 在这种情况下,我们只需要为A构造一次哈希,就可以使用其即时搜索将其与所考虑的所有集合B的元素进行比较。
性能测试
通过实践来确认该理论总是有用的(特别是在类似后者的情况下,当尚不清楚哈希的初始成本是否会随着搜索性能的提高而获得回报时)。
在我的测试中,第一个选项(对两个集合进行排序)始终显示最差的结果。 仅对一个较小的集合进行排序在相同大小的集合上效果要好一些,但并不过分。 但是,第二个和第三个算法在其中一个集合比另一个集合大1000倍的情况下,生产率显着提高(大约6倍)。