我们将继续围绕Monero区块链设备的周期,今天的文章将专门介绍RingCT协议(Ring Secret Transactions),该协议介绍了机密交易和新的环签名。 不幸的是,Internet上几乎没有有关其工作方式的信息,因此我们试图填补这一空白。

我们将讨论网络如何使用此协议隐藏传输量,为什么我们拒绝经典的加密货币环签名以及该技术将如何进一步发展。
由于此协议是门罗币中最复杂的技术之一,因此读者将需要有关此区块链设备的基础知识以及椭圆曲线上的密码学浅表知识(要刷新此知识,您可以阅读上一篇有关
多重签名的文章的第一章)。
RingCT协议
对加密货币的可能攻击之一是基于对已发送交易的数量和时间的了解的区块链分析。 它允许
大大缩小了攻击者感兴趣的输出的搜索范围。 为了防止此类分析,Monero引入了一种匿名交易协议,该协议完全隐藏了网络上的传输量。
值得注意的是,隐藏金额的想法并不新鲜。 最早描述它的人之一是比特币核心开发人员Greg Maxwell在他的《
保密交易》文章中 。 RingCT的当前实现是对它的修改,可以使用环签名(不使用环签名),因此得名-Ring Confidential Transactions。
除其他事项外,该协议有助于消除混合粉尘输出的问题-少量输出(通常以交易的形式从变化中获得),这会产生比其本身成本更多的问题。
2017年1月,举行了Monero硬分叉网络,允许随意使用机密交易。 同年9月,使用版本6的硬分叉,此类交易成为网络上唯一允许的交易。
RingCT一次使用多种机制:多层可链接的自发匿名组签名(以下称为MLSAG),Pedersen承诺和范围证明(该术语没有确定的俄语翻译)。
RingCT协议引入了两种类型的匿名事务:简单和完全。 当交易使用多个输入时,第一个钱包生成,第二个钱包在相反的情况下生成。 它们在交易金额和MLSAG签名所签名的数据的验证方面有所不同(我们将在下文中详细讨论)。 而且,完全类型的交易可以用任意数量的输入生成,没有根本的区别。 关于这一主题的
“从零到门罗币为零”一书说,将全部交易限制为一次输入的决定是仓促作出的,将来可能会改变。
MLSAG签名
回想一下交易的签名输入是什么。 每笔交易都花一些钱并产生。 通过创建交易输出来产生资金(直接类比为钞票),而交易花费的输出(毕竟,在现实生活中我们正在花费钞票)成为输入(小心,在这里很容易混淆)。
入口是指多个出口,但仅花费一个出口,因此创建了一个“烟幕”,使分析翻译历史变得困难。 如果一个事务有多个输入,则可以以矩阵的形式表示这种结构,其中行是输入,列是捏合输出。 为了向网络证明交易花费了其输出(知道其秘密密钥),请使用环签名对输入进行签名。 这样的签名可以保证签名者知道任何列中所有元素的秘密密钥。
机密交易不再使用传统的
加密纸币环签名,它们已被MLSAG取代,MLSAG是类似的单层环签名
LSAG的多输入版本。
之所以称它们为多层,是因为它们一次对多个输入进行签名,每个输入都与其他多个输入混合,也就是说,矩阵是有符号的,而不是一行。 稍后我们将看到,这有助于节省签名的大小。
让我们以交易为例看一下环签名的形成方式,该交易花费2个实际输出,并使用m-1个从区块链到捏合的随机输出。 表示我们花费的输出的公钥
,以及它们的关键图像:
这样,我们得到一个
2 x m的矩阵。 首先,我们需要为每对输出计算所谓的挑战:
我们从使用其公钥花费的输出开始计算:
和随机数
结果,我们得到了以下值:
我们用来计算挑战的
下一对输出(为了更容易理解我们要替换的位置,我们以不同的颜色突出显示了这些值)。 根据第一个插图中给出的公式,将所有以下所有值围成一个圆计算。 最后计算一对实际输出的挑战。
如我们所见,在所有列中,除了包含实际输出的那一列之外,均使用随机生成的数字
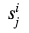
。 对于第π列,我们也需要它们。 转换
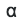
在s:
签名本身就是所有这些值的元组:
此外,该数据被写入事务中。
如我们所见,MLSAG仅包含一个质询
c 0 ,从而节省了签名的大小(该签名已经需要大量空间)。 接下来,使用数据的任何审阅者
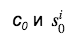
,恢复值c
1 ,...,c
m并验证

。 因此,我们的戒指被关闭,签名通过了验证。
对于full类型的RingCT事务,将在混合输出的矩阵中再增加一行,但是我们将在下面讨论。
Pedersen的承诺
使用承诺方案 (通常使用英文术语-承诺),以便一方可以证明自己知道某个秘密(数字),而无需实际透露它。 例如,您在骨头上扔了一定数量,考虑承诺并将其传递给依赖方。 因此,在透露机密号码时,检查员会独立考虑承诺,从而确保您没有欺骗他。
门罗币承诺用于隐藏转账金额并使用最常见的选项-彼德森承诺。 顺便说一句,一个奇怪的事实-首先,开发人员建议使用通常的捏合方法隐藏金额,即将输出添加到任意金额以引入不确定性,但随后转而使用承诺(这并不是事实,他们节省了交易规模,如下所示)。
通常,承诺如下:
其中
C是承诺本身的值,
a是要隐藏的数量,
H是椭圆曲线上的固定点(附加生成器),
x是隐藏随机生成的因子的任意掩码。 这里需要使用掩码,以使第三方无法通过简单的蛮力选择承诺的价值。
生成新的退出时,钱包会为此计算出一个承诺,而在支出时,它会根据生成的类型采用生成期间计算出的值,或再次对其进行重新计数。
Ringct简单
对于简单的RingCT交易,为了确保该交易创建的输出等于输入的总和(不是从空中赚钱),第一笔和第二笔的承诺应相同,即:
承诺委员会认为有些不同-没有遮罩:
,其中
a是佣金的金额,可公开获得。
这种方法使我们能够向依赖方证明我们使用了相同的数量而不泄露它们。
为了使事情更清楚,让我们看一个例子。 假设事务在10个和5个XMR上花费了两个输出(即它们成为输入),并生成了三个输出,总共12个XMR:3个,4个和5个XMR。 同时支付3 XMR的佣金。 因此,所花费的金额加上所产生的金额和佣金等于15 XMR。 让我们尝试计算承诺并查看承诺金额的差异(记住数学):
在这里,我们看到方程收敛—我们需要的输入和输出的掩码之和是相同的。 为此,钱包会随机生成
x 1 ,y 1 ,y 2和y 3 ,其余的
x 2会这样计算:
使用这些蒙版,我们可以向任何检查过的人证明,在不透露金额的情况下,我们产生的资金不会超过我们的支出。 原来是吧?
RingCT已满
在完整的RingCT交易中,检查转账金额更为复杂。 在这些交易中,钱包不计入入账承诺,而是使用生成承诺时计算出的承诺。 在这种情况下,我们必须假设我们所获得的金额之差不再等于零,而是:
z是输入和输出的掩码之间的差。 如果我们将
zG视为公钥(实际上是),则
z是私钥。 因此,我们知道公钥和相应的私钥。 有了这些数据,我们可以将其与揉捏输出的公钥一起用于MLSAG环形签名中:
因此,有效的环签名将保证我们知道其中一列的所有私钥,并且仅当交易产生的资金不超过其支出的费用时,我们才能知道最后一行的私钥。 顺便说一下,这是对以下问题的答案:“为什么承诺量的差异没有导致零”-如果
zG = 0 ,那么我们将使用实际输出打开该列。
但是收款人怎么知道他们寄给他多少钱呢? 这里的一切都很简单-交易的发送者和接收者使用Diffie-Hellman协议交换密钥,使用接收者的交易密钥和查看密钥,并计算共享机密。 发送者将使用此共享密钥加密的输出总和写入交易数据的特殊字段中。
范围证明
但是,如果您使用负数作为承诺金额会怎样? 这可以导致产生额外的硬币! 这样的结果是不可接受的,因此,我们需要保证我们使用的金额不为负(当然,不披露这些金额,否则会花费很多精力,而且都是徒劳的)。 换句话说,我们必须证明和在区间
[0,2 n -1]中 。
为此,将每个输出的总和划分为二进制数字,并分别考虑每个数字的承诺。 这是如何发生的,最好考虑一个例子。
假设我们有少量并且适合4位(实际上是64位),并且我们创建了5 XMR量的输出。 我们考虑每个类别的承诺以及全部金额的一般承诺:
此外,每个承诺都混合有代理人
(C i -2 i H) ,并由Greg Maxwell在2015年提出的Borromeo环签名(另一个环签名)成对签名(有关更多信息,请参见
此处 ):
一起,这称为范围证明,并确保承诺使用区间
[0,2 n -1]中的量 。
接下来是什么?
在当前的实现中,范围证明占用大量空间-每个输出6176字节。 这导致大量交易,并因此导致更高的佣金。 为了减小Monero的交易规模,开发人员正在引入Borromeo签名而不是Borromeo签名-范围证明机制,没有按位承诺。
根据一些估计 ,他们可以将范围证明大小减小到94%。 顺便说一下,在7月中旬,该技术已由Kudelski Security进行了
审核 ,该技术并未发现该技术本身或实施方面的任何重大缺陷。 该技术已经在测试网络中使用,并且有了新的硬分叉,它很可能可以迁移到主网络。
提出您的问题,为有关加密货币技术的新文章提出主题,并在
Facebook上订阅我们的小组以了解我们的事件和出版物。