选择排序的想法是什么？

在未排序的子数组中，寻求局部最大值（最小值）。
找到的最大（最小）变化与子数组中最后一个（第一个）元素的位置。
如果未排序的子数组保留在数组中，请参见第1点。

轻微的抒情偏离。最初，在我的系列文章中，我计划以严格的顺序一致地介绍有关分类的材料。在库排序之后，计划了有关其他插入算法的文章：单人纸牌排序，按Young表排序，通过反转排序等。

但是，现在的趋势是非线性，因此，在不编写所有有关按插入排序的出版物的情况下，今天，我将开始一个关于按选择排序的并行分支。然后，我将对其他算法类执行相同的操作：合并排序，分布排序等。通常，这将使出版物可以在一个主题上写，然后在另一个主题上写。有了这样的主题旋转，将会更加有趣。

选择排序

简单且朴实无华-我们遍历数组以查找最大元素。找到的最大值与最后一个元素互换。数组的未排序部分减少了一个元素（不包括我们重新排列找到的最大值的最后一个元素）。我们对未排序的部分应用相同的操作-我们找到最大值并将其放在数组未排序的部分的最后位置。因此，我们继续进行操作，直到数组的未排序部分减少为一个元素为止。

def selection(data): for i, e in enumerate(data): mn = min(range(i, len(data)), key=data.__getitem__) data[i], data[mn] = data[mn], e return data

用简单的选择进行排序是一个粗略的双重搜索。可以改善吗？让我们看一些修改。

双重选择排序::双重选择排序

振动筛分选中使用了类似的想法，这是气泡分选的变体。除了最大值以外，通过数组的未排序部分，我们还同时找到了最小值。我们将最小值放在首位，将最大值放在最后。因此，每次迭代中未排序的部分会同时减少两个元素。

乍一看，这似乎使算法加快了2倍-每次通过后，未排序的子数组不是从一个而是从两个侧面一次减少的。但与此同时，比较次数增加了2倍，掉期次数保持不变。双重选择只会稍微提高算法的速度，在某些语言中，由于某些原因，它甚至会变慢。

选择插入排序与插入排序的区别

似乎按选择排序和按插入排序是一回事，这是一类常见的算法。好吧，或者按插入排序是一种选择排序。或者按选择排序是按插入排序的一种特殊情况。在那儿，我们从数组的未排序部分轮流提取元素并将它们重定向到已排序区域。

主要区别在于：通过插入排序时，我们从数组的未排序部分提取任何元素，并将其插入到已排序部分的位置。在选择排序中，我们有目的地寻找与数组的排序部分互补的最大元素（或最小元素）。在插图中，我们正在寻找下一个元素的插入位置，在选择中-我们已经预先知道要放置在哪个位置，但是与此同时，我们需要找到与该位置对应的元素。

这使得两类算法的本质和所用方法完全不同。

宾果排序::宾果排序

排序选择的一个有趣特征是排序数据的性质与速度无关。

例如，如果数组几乎已排序，那么，如您所知，按插入顺序排序将更快地处理它（甚至比快速排序还快）。按插入顺序排序的逆序数组是一种简并的情况，它将尽可能长地对其进行排序。

对于通过选择进行排序，数组的部分或反向排序不起作用-它会以与常规随机数组相同的速度处理数组。另外，对于经典排序，数组由唯一或重复的元素组成也没关系-这实际上不会影响速度。

但是原则上，您可以设计和修改算法，以便它在处理某些数据集时更快。例如，如果数组由重复元素组成，则将宾果排序考虑在内。

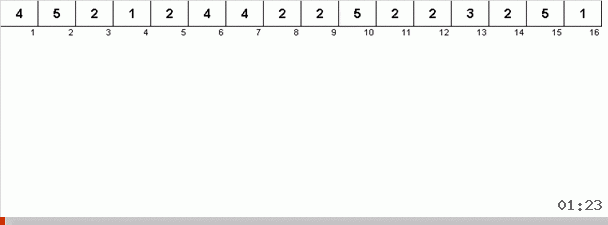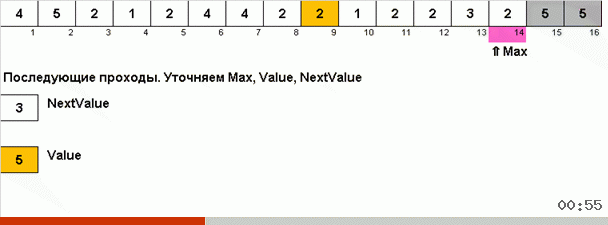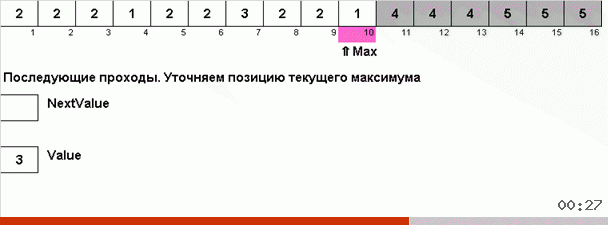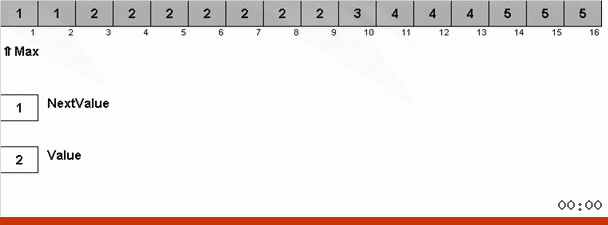
这里的技巧是不仅在无序部分中记住最大元素，而且还要确定下一次迭代的最大值。这允许重复的最大值而不是每次都再次搜索它们，而是在数组中再次遇到该最大值时将它们放置在它们的位置。

算法复杂度保持不变。但是，如果数组由重复数字组成，则宾果排序的速度将比按选择的常规排序快十倍。

 # - def bingo(data): #  . max = len(data) - 1 nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 #  . while max: value = nextValue nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] == value: data[i], data[max] = data[max], data[i] max -= 1 elif data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 return data

循环排序::循环排序

循环排序很有趣（从实际的角度来看很有价值），因为只有当元素放在其最终位置时，数组元素之间才会发生变化。如果在阵列中重写太昂贵，并且要照顾物理内存，则需要最大程度地减少对阵列元素的更改次数，这可能会派上用场。

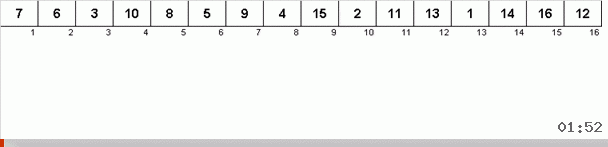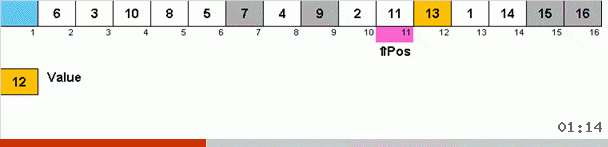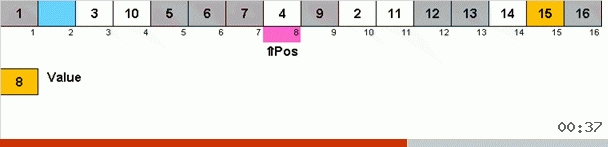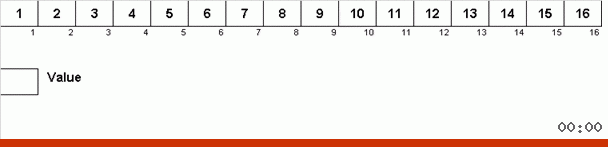
它是这样的。我们对数组进行排序，在此外循环中将X称为下一个单元格。然后，我们查看需要在数组中的哪个位置插入此单元格中的下一个元素。在您要粘贴其他元素的位置，我们将其发送到剪贴板。对于缓冲区中的此元素，我们还将在数组中查找其位置（并将其粘贴到此位置，并将出现在此位置的元素发送到缓冲区）。对于缓冲区中的新数字，我们执行相同的操作。此过程应持续多长时间？直到剪贴板中的下一个元素变成需要在单元格X中精确插入的元素（算法主循环中数组的当前位置）。迟早会发生这一刻，然后在外循环中，您可以转到下一个单元格并为其重复相同的过程。

在其他类型中，通过选择，我们会寻找最大值/最小值以将它们放在最后/第一位。在循环排序中，事实证明，在将其他几个元素放置在数组中间某个适当位置的过程中，子数组中的至少第一个位置仍是如此。

在这里，算法复杂度也保持在O（ n ² ）内。在实践中，循环排序的效果甚至比选择的常规排序还要慢几倍，因为您必须更多地围绕数组运行并且更频繁地进行比较。这是尽可能少的重写次数的价格。

 #   def cycle(data): #        for cycleStart in range(0, len(data) - 1): value = data[cycleStart] # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      ,   #      if pos == cycleStart: continue #   ,     #        while value == data[pos]: pos += 1 data[pos], value = value, data[pos] #      , #         while pos != cycleStart: # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      #      while value == data[pos]: pos += 1 data[pos], value = value, data[pos] return data

薄煎饼排序

该算法已掌握了从细菌到比尔·盖茨的所有生命水平。

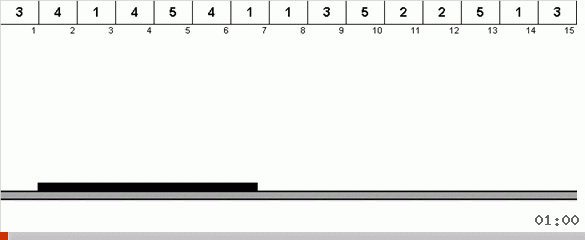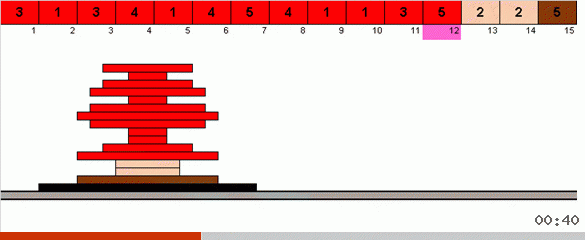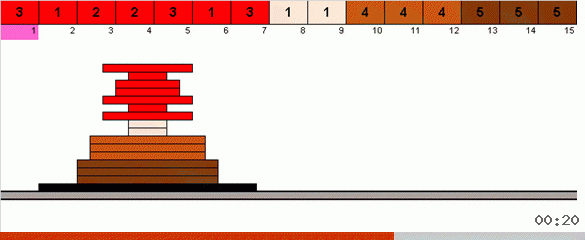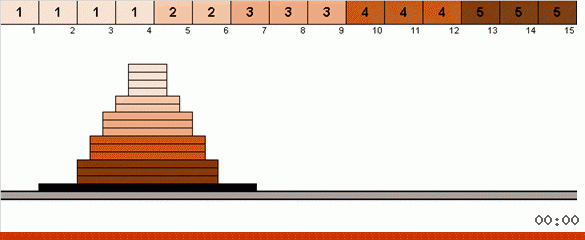
在最简单的情况下，我们正在数组的未排序部分中寻找最大元素。找到最大值后，我们进行两次急转弯。首先，我们旋转元素链，以使最大值位于另一端。然后，我们翻转整个未排序的子数组，其结果是最大值落在适当的位置。

一般来说，这种炸弹导致算法复杂度为O（ n ³ ）。这些受过训练的纤毛一口气翻滚（因此，执行时的复杂度为O（ n ² ）），并且在编程时，阵列部分的反转是一个附加的周期。

从数学的角度来看，煎饼分类非常有趣（最好的主意是考虑评估足以进行分类的最小翻转次数），还有更复杂的问题表达方式（所谓的一侧烧坏了）。煎饼的话题非常有趣，也许我会针对这些问题撰写更全面的专着。

 #   def pancake(data): if len(data) > 1: for size in range(len(data), 1, -1): #      maxindex = max(range(size), key = data.__getitem__) if maxindex + 1 != size: #    ,    if maxindex != 0: #  , #     data[:maxindex+1] = reversed(data[:maxindex+1]) #    , #      data[:size] = reversed(data[:size]) return data

选择排序与组织数组未排序部分中的最小/最大元素的搜索一样有效。在当今分析的所有算法中，搜索都是以双重搜索的形式进行的。在双重搜索中，无论怎么说，算法复杂度始终不会比O（ n ² ）好。这是否意味着所有选择都注定要表示平方复杂度？完全没有，如果搜索过程是以根本不同的方式组织的。例如，将数据集视为堆并在堆上搜索。但是，堆的主题甚至不是一篇文章，而是一个完整的传奇故事，我们肯定会谈论堆，但这是另一回事。

参考文献

选择 / 循环，煎饼 / 煎饼

系列文章：

Excel应用程序AlgoLab.xlsm
交换排序
插入排序
按选择排序
- 二进制堆排序和修改
- 二项式和弱堆排序
- 比赛排序
- 笛卡尔树排序
- 丛林排序
- 按选择比较排序
合并排序
按分布排序
混合排序

今天的宾果游戏，脚踏车和煎饼已经添加到了AlgoLab应用中。在后者中，与煎饼的绘制有关，已设置了一个限制-数组中元素的值应为1到5。您当然可以放置更多，但是宏将随机采用该范围内的数字。

按选择排序