有一系列样本
x 0 ,x 1 ,x 2 , \点。 此外,如前所述,有两个初始参数
ÿ 0 和
s 0 。 需要获取新的样本序列
y 0 ,y 1 ,y 2 \点 。 您已经猜到了,第一个输出样本是已知的:它与一个初始参数一致
ÿ 0 。 这不是“初始位移”。 值得注意的是,输入(源)样本被编码为四个比特。 对于有符号类型,从-8到7(包括8和7)之间的整数属于编码范围。 实际上,最高有效位是造成数字符号的原因。 解码后获得的输出PCM样本具有带符号的16位标准格式。
分析C语言中的算法代码,您可以看到两个表。 它们在下面列出。
int ima_index_table[] = { -1, -1, -1, -1, 2, 4, 6, 8 };
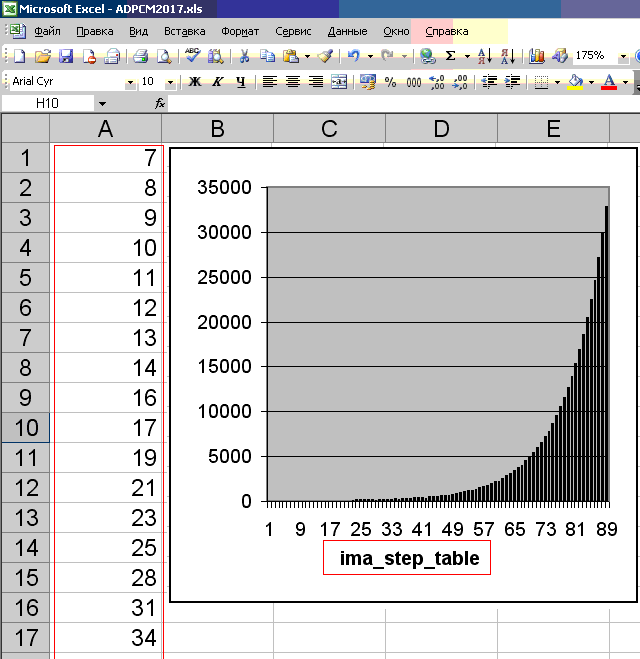
int ima_step_table[] = { 7, 8, 9, 10, 11, 12, 13, 14, 16, 17, 19, 21, 23, 25, 28, 31, 34, 37, 41, 45, 50, 55, 60, 66, 73, 80, 88, 97, 107, 118, 130, 143, 157, 173, 190, 209, 230, 253, 279, 307, 337, 371, 408, 449, 494, 544, 598, 658, 724, 796, 876, 963, 1060, 1166, 1282, 1411, 1552, 1707, 1878, 2066, 2272, 2499, 2749, 3024, 3327, 3660, 4026, 4428, 4871, 5358, 5894, 6484, 7132, 7845, 8630, 9493, 10442, 11487, 12635, 13899, 15289, 16818, 18500, 20350, 22385, 24623, 27086, 29794, 32767 };
可以说,这两个“魔术”数组是表格函数,在其参数中替换了相同的两个初始参数。 在迭代过程中,每一步都将重新计算参数,并将其再次代入这些表中。 首先,让我们看看如何在代码中实现它。
我们声明必要的,包括辅助变量。
int current1; int step; int stepindex1; int diff; int current; int stepindex; int value;
在开始迭代之前,您需要将初始参数分配给当前变量
ÿ 0 ,而变量stepindex为
s 0 。 这是在相关算法之外完成的,因此我不会在代码中反映出来。 以下是循环(循环)执行的转换。
value = read(input_sample);
在ima_step_table数组的辅助变量step中,写入索引stepindex1的值。 对于第一次迭代,这是初始参数
s 0 ,对于进一步的迭代,这是一个重新计算的参数
si 。 然后,通过向右移位操作将该数组中的值除以8(显然是完全),并且由于该除法而将diff变量初始化。 然后,分析输入样本值的三个最低有效位,并且根据它们的状态,可以通过三个项来调整diff变量。 这些术语是diff值由4(>> 2),2(>> 1)或diff不变的相似整数除法(一般情况下为1除法)。 然后,分析输入样本值的最高有效(有符号)位。 根据其状态,将在此变量之前生成的diff变量添加或减去到变量current1中。 这将是输出样本的值。 为了正确起见,这些值仅限于顶部和底部。 然后,通过将ima_index_table数组中的值与输入样本的值的索引相加(符号位重置为零)来调整stepindex1。 Stepindex1值也受限制。 最后,在重复此算法之前,将当前和stepindex值分配给刚重计数的current1和stepindex1值,然后再次重复该算法。
您可以尝试解决这个问题,以便大致了解diff变量的形成方式。 让
fi=f(si) 。 这些是迭代的每个第i步的step变量的值,作为参数的函数(数组)的值
si 在哪里
i=0、1、2,\点 。 为了方便起见,我们将diff变量表示为
d 。 按照上述推理的逻辑,我们有:
di= fracfi8+x(0)i fracfi4+x(1)i fracfi2+x(2)ifi,
在哪里
x(0)i,x(1)i,x(2)i -数字的低3位
xi 。 导致一个公分母,我们将此表达式转换为更方便的形式:
di= fracfi8 Bigg(1+2x(0)i+4x(1)i+8x(2)i Bigg)=
= fracfi8 Bigg(1+2 Big(x(0)i+2x(1)i+4x(2)i Big) Bigg)= fracfi8(2xi+1)
最后一次转换基于以下事实:在某种意义上,数字的最低三位(0或1)
xi 使用给出的系数,除了写出该数字的绝对值以及该数字的最高有效位外,还有其他事情
xi 将匹配整个表达式的符号。 进一步根据公式
yi+1=yi+di
根据旧样本值计算出一个新样本值。 另外,将计算一个新的变量值。
s :
si+1=si+t(|xi|)
公式中的模块指示变量
xi 起作用
t 不包括最高有效符号位,这在代码中得到了体现。 功能
t 是ima_index_table数组的值,索引与该参数对应。
在公式的描述中,我忽略了上面和下面的限制操作。 总迭代方案如下所示:
y0; s0; x0,x1,x2,\点
di= fracf(si)8\大(2xi+1\大)
yi+1=yi+di
si+1=si+t(|xi|)
i=0、1、2,\点
我没有深入研究编码/解码ADPCM的理论。 但是,ima_step_table数组(共89个)的表值通过它们在图形上的反射(请参见下图)判断,描述了相对于零线的样本的概率分布。 实际上,通常是这样:样本越靠近零线,发生的次数就越多。 因此,ADPCM是基于概率模型的,决不能将任何16位PCM样本源集正确地转换为4位ADPCM样本。 一般来说,ADPCM是具有可变量化步长的PCM。 显然,该图表反映了这一非常可变的步骤。 在实践中,根据音频数据的分布规律正确选择了他。