用于模型训练的数据（不类似于样本）多少？

考虑一种您的机器学习模型可能一文不值的情况。

有句俗话： “不要把苹果和桔子相提并论 。 ” 但是，如果您需要将一组苹果与橙子与另一组苹果进行比较，但是两组水果的分配不同，该怎么办呢？ 您可以使用数据吗？ 您将如何做？


在实际情况下，这种情况很常见。 在开发机器学习模型时，我们会遇到这样的情况，即我们的模型在训练集中可以很好地工作，但是模型的质量在测试数据上急剧下降。

这与再培训无关。 假设我们建立了一个模型，该模型在交叉验证中给出了出色的结果，但是在测试中却显示出了差的结果。 因此，在测试样本中有一些我们没有考虑的信息。

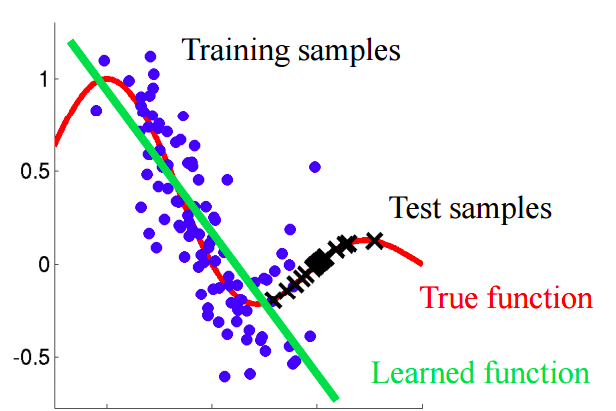
想象一下我们预测商店中顾客行为的情况。 如果训练样本和测试样本如下图所示，这是一个明显的问题：


在此示例中，模型在属性“客户年龄”的平均值低于测试中类似属性的平均值的数据上训练。 在学习过程中，模型从未“看到”“ age”属性的较大值。 如果年龄是模型的重要特征，则不应期望测试样品获得良好的结果。

在本文中，我们将讨论“天真的”方法，这些方法使我们能够识别并消除这些现象。

协变移位

让我们对这个概念给出更准确的定义。 协方差是指特征值， 协方差移位是指训练样本和测试样本中的特征值分布具有不同特征（参数）的情况。

在具有大量变量的实际问题中，协变量偏移难以检测。 本文讨论了用于识别以及说明数据中协变偏移的方法。

主要思想

如果数据发生偏移，则在将两个样本混合时，我们可以构建一个分类器，以确定对象是否属于训练样本或测试样本。


让我们了解为什么会这样。 让我们以客户为例，年龄是培训和测试样本的“转变”标志。 如果我们采用分类器（例如，基于随机森林）并尝试将混合样本分为训练和测试，那么年龄将是此类分类的一个非常重要的标志。

实作

让我们尝试将描述的想法应用于真实数据集。 使用Kaggle竞赛中的数据集 。

步骤1：资料准备

首先，我们将遵循一系列标准步骤：清洁，填入空白处，对分类标志进行标签编码。 所需数据集无需执行任何步骤，因此请跳过其描述。

import pandas as pd #  train  test train = pd.read_csv('train.csv',low_memory=True) test = pd.read_csv('test.csv',low_memory=True) 

步骤2：添加数据源指示器

有必要向数据集的两个部分（培训和测试）添加新的指标指标。 对于值为“ 1”的训练样本，对于测试，分别为“ 0”。

 #    ,   test,   train test['is_train'] = 0 train['is_train'] = 1 

步骤3：结合学习样本和测试样本

现在，您需要组合两个数据集。 由于训练数据集包含目标值“ target”的列，该列不在测试数据集中，因此必须删除此列。

 #  train, test df_combine = pd.concat([train, test], axis=0, ignore_index=True) #  target df_combine = df_combine.drop('target', axis =1) y = df_combine['is_train'].values #  x = df_combine.drop('is_train', axis=1).values #  tst, trn = test.values, train.values 

步骤4：建立和测试分类器

为了进行分类，我们将使用“随机森林分类器”，将其配置为预测组合数据集中数据源的标签。 您可以使用任何其他分类器。

 from sklearn.ensemble import RandomForestClassifier import numpy as np rfc = RandomForestClassifier(n_jobs=-1, max_depth=5, min_samples_leaf = 5) predictions = np.zeros(y.shape) #     

我们使用4层分层随机分组。 这样，我们将像原始合并的样本一样，保持每个折叠中“ is_train”标签的比率。 对于每个分区，我们在大部分分区上训练分类器，并为较小的递延部分预测分类标签。

 from sklearn.model_selection import StratifiedKFold, cross_val_score skf = StratifiedKFold(n_splits=4, shuffle=True, random_state=100) for fold, (train_idx, test_idx) in enumerate(skf.split(x, y)): X_train, X_test = x[train_idx], x[test_idx] y_train, y_test = y[train_idx], y[test_idx] rfc.fit(X_train, y_train) probs = rfc.predict_proba(X_test)[:, 1] #   predictions[test_idx] = probs 

步骤5：解释结果

我们为分类器计算ROC AUC指标的值。 基于此值，我们得出结论，我们的分类器显示数据的协变程度如何。

如果分类器c将对象很好地分为训练和测试数据集，则ROC AUC度量的值应显着大于0.5，理想情况下应接近1。此图表明数据中有很强的协变偏移。

查找ROC AUC的值：

 from sklearn.metrics import roc_auc_score print('ROC-AUC:', roc_auc_score(y_true=y, y_score=predictions)) # ROC-AUC: 0.49974692698385287 

结果值接近0.5。 这意味着我们的质量分类器与随机标签预测器相同。 没有证据表明数据发生了协变。

由于数据集来自Kaggle，因此结果是可以预料的。 与其他机器学习竞赛一样，对数据进行仔细验证以确保不发生任何变化。

但是，这种方法可以应用到数据科学的其他问题中，以在解决方案开始之前检查是否存在协变偏移。

进一步的步骤

因此，我们是否观察到协变偏移。 如何提高测试中模型的质量？

1. 删除有偏见的功能
2. 根据密度系数估算值使用对象重要性权重

删除有偏差的功能：

注意：如果数据存在协变偏移，则该方法适用。

• 从我们之前构建和训练的随机森林分类器中提取属性的重要性。
• 最重要的标志恰好是那些有偏见并导致数据移位的标志。
• 首先从最重要的角度出发，一次删除，构建目标模型并查看其质量。 收集所有不会降低模型质量的标志。
• 丢弃数据中收集的特征并建立最终模型。

该算法允许您从图中的红色篮子中删除符号。

根据密度系数估算值使用对象重要性权重

注意：无论数据中是否存在协变移位，该方法均适用。

让我们看看上一节中收到的预测。 对于每个对象，预测都包含该对象属于我们的分类器训练集的概率。

 predictions[:10] #array([0.39743827 ... 

例如，对于第一个对象，我们的随机森林分类器认为它属于训练集，概率为0.397。 叫这个值 $$$P（火车）$。 或者我们可以说属于测试数据的概率为0.603。 同样，我们称概率 $$$P（测试）$。

现在有一个小技巧：对于训练数据集的每个对象，我们计算系数 $$$w = \ frac {P（测试）} {P（火车）}$。

系数 $$$w$告诉我们距离训练集中的对象距测试数据有多近。 主要思想：

我们可以使用 $$$w$像任何模型中的权重一样，以增加看起来类似于测试样本的那些观测值的权重。 直观上讲，这是有道理的，因为我们的模型将像测试套件中那样更加面向数据。

可以使用以下代码计算这些权重：

 import seaborn as sns import matplotlib.pyplot as plt plt.figure(figsize=(20,10)) predictions_train = predictions[:len(trn)] weights = (1./predictions_train) - 1. weights /= np.mean(weights) #  plt.xlabel('  w') plt.ylabel(' ') sns.distplot(weights, kde=False) 

可以将获得的系数转移到模型中，例如，如下所示：

 rfc = RandomForestClassifier(n_jobs=-1,max_depth=5) m.fit(X_train, y_train, sample_weight=weights) 

关于结果直方图的几句话：

• 较大的重量值对应于更类似于测试样品的观察值。
• 训练集中几乎70％的对象的权重接近1，因此位于与训练集和测试集相似的子空间中。 这对应于我们之前计算的AUC值。

结论

我们希望这篇文章能帮助您识别数据中的“协变偏移”并加以应对。

参考文献

[1] Shimodaira，H.（2000）。 通过加权对数似然函数来改善协变量偏移下的预测推理。 统计计划与推断杂志，90，227-244。
[2] Bickel，S.等。 （2009）。 协变量移位下的判别学习。 机器学习研究杂志，10，2137–2155
[3] github.com/erlendd/covariate-shift-adaption
[4] 链接到使用的数据集

PS：带有本文代码的笔记本电脑可以在此处查看。