理查德·汉明（Richard Hamming）：第13章。信息论

我们做到了！

“本课程的目标是为您的技术未来做好准备。”

哈Ha 还记得那篇很棒的文章“您和您的工作” （+219，添加了2588书签，读取了429k）吗？

因此，汉明（是的，是的，自我检查和自我纠正的汉明代码 ）根据他的演讲编写了一整本书 。 我们正在翻译它，因为那个人在谈论生意。

这本书不仅是关于IT的书，还是关于令人难以置信的酷人的思维方式的书。 “这不仅仅是积极思考的冲动； 它描述了增加做出色工作机会的条件。”

感谢您翻译成Andrei Pakhomov。

信息理论是C.E. Shannon在1940年代后期提出的。 贝尔实验室管理层坚持称其为“通信理论”，因为 这是一个更准确的名称。 由于明显的原因，“信息理论”这个名称对公众的影响更大，因此，香农选择了它，这是我们今天所知道的。 这个名称本身就暗示了该理论涉及信息，这很重要，因为我们正在更深入地渗透到信息时代。 在本章中，我将介绍该理论的一些基本结论，我将不提供严格但直观的证据来证明该理论的某些单独规定，以便您了解“信息理论”的实际含义，可以在何处应用和不可以在何处使用。 。

首先，什么是“信息”？ 香农识别具有不确定性的信息。 他选择了事件概率的负对数，作为事件以概率p发生时收到的信息的定量度量。 例如，如果我告诉您洛杉矶的天气是多雾的，则p接近1，这基本上不能给我们太多信息。 但是，如果我说六月的蒙特雷下雨，那么这则消息将充满不确定性，并且它将包含更多信息。 可靠事件不包含任何信息，因为log 1 = 0。

让我们更详细地讨论这一点。 香农认为，信息的定量度量应该是事件p的概率的连续函数，对于独立事件，它应该是累加的-两个独立事件的结果所获得的信息量应等于联合事件所获得的信息量。 例如，掷骰子和硬币的结果通常被视为独立事件。 让我们将以上内容翻译成数学语言。 如果I（p）是概率为p的事件中包含的信息量，则对于由两个独立事件x和概率p ₂组成的联合事件，我们得到：


（x和y个独立事件）

这是函数柯西方程，对于所有p ₁和p2都是正确的。 为了解决这个函数方程，假设

p ₁ = p ₂ = p，

它给



如果p ₁ = p ²且p ₂ = p，则



等 使用标准方法对所有有理数m / n的指数进行扩展，以下是正确的



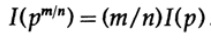
从信息测度的假定连续性可以得出，对数函数是函数柯西方程的唯一连续解。

在信息论中，习惯上以2的对数为底，因此二进制选择恰好包含1位信息。 因此，信息是通过公式来衡量的



让我们暂停一下，看看上面发生了什么。 首先，我们没有对“信息”的概念进行定义，我们只是为其定量度量定义了一个公式。

其次，此措施取决于不确定性，尽管它足够适用于机器（例如电话系统，无线电，电视，计算机等），但它并不能反映人类对信息的正常态度。

第三，这是一个相对的措施，取决于您当前的知识状态。 如果查看随机数生成器中的“随机数”流，则假定每个下一个数都是不确定的，但是如果您知道计算“随机数”的公式，则下一个数将是已知的，因此将不包含信息。

因此，香农给出的信息定义在许多情况下都适用于机器，但似乎不符合人类对该词的理解。 因此，“信息论”应称为“通信论”。 但是，更改定义为时已晚（感谢该理论最初得到普及，并且仍然使人们认为该理论涉及“信息”），因此我们必须忍受它们，但是您必须清楚地了解香农给出的信息定义与常识相差多远。 香农的信息处理的是完全不同的东西，即不确定性。

这是您提供任何术语时需要考虑的问题。 提议的定义（例如Shannon给出的定义）与您的原始想法之间的一致性如何？它有何不同？ 几乎没有一个术语可以准确地反映出您对该概念的早期理解，但是最后，所使用的术语反映了该概念的含义，因此通过清晰的定义对某些事物进行形式化总是会带来一些噪音。

考虑一个系统，其字母由概率为pi的符号q组成。 在这种情况下，系统中的平均信息量 （其期望值）为：



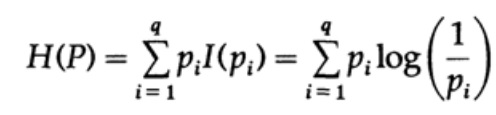
这称为概率分布系统{pi}的熵。 我们使用“熵”一词是因为在热力学和统计力学中出现了相同的数学形式。 这就是为什么“熵”一词在自身周围创造出一个重要光环的原因，而这一光环最终是不合理的。 相同的数学符号形式并不意味着对字符的相同解释！

概率分布的熵在编码理论中起主要作用。 两个不同的概率分布pi和qi的Gibbs不等式是该理论的重要结果之一。 所以我们必须证明



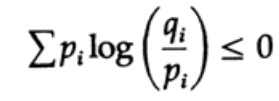
证明基于一个明显的图形，图。 13.I，表明



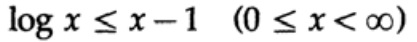
并且仅当x = 1时才达到等式。我们将不等式应用于左侧总和的每个被加数：



如果通信系统的字母由q个字符组成，则以每个字符qi = 1 / q的传输概率并代入q，我们从吉布斯不等式中获得





图13.I

这表明如果传输所有q个字符的概率相同且等于-1 / q，则最大熵为ln q，否则不等式成立。

对于唯一解码的代码，我们有卡夫不等式



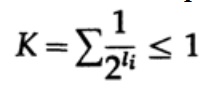
现在，如果我们定义伪概率



当然在哪里 = 1，这是根据吉布斯不等式得出的，



并应用一些代数（请记住，K≤1，因此我们可以省略对数项，并可能在以后加强不等式），



其中L是代码的平均长度。

因此，熵是具有平均码字L的任何字符码的最小边界。这是信道的无干扰香农定理。

现在我们考虑关于通信系统的局限性的主要定理，在该系统中，信息以独立比特流的形式传输，并且存在噪声。 这意味着正确传输一位的概率为P> 1/2，并且在传输过程中发生错误的位值被反转的概率为Q = 1-P。为方便起见，我们假设错误是独立的，并且每次发送的错误概率均相同位-即，通信通道中存在“白噪声”。

我们在一条消息中编码的n位长数据流的方式是一位代码的n维扩展。 我们稍后将确定n的值。 将包含n位的消息视为n维空间中的一个点。 由于我们有一个n维空间-为简单起见，我们假设每个消息都有相同的出现概率-有M个可能的消息（M也会在以后确定），因此，任何已发送消息的概率等于




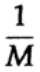
（发件人）
图13.II

接下来，考虑信道带宽的思想。 在不赘述的情况下，考虑到使用最有效的编码，将信道容量定义为可以在通信信道上可靠地传输的最大信息量。 毫无疑问，通过通信通道可以传输的信息超过其容量。 对于二进制对称通道（我们在本例中使用的通道）可以证明这一点。 按位发送的信道容量设置为



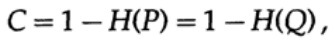
如前所述，其中P是任何发送的比特中没有错误的概率。 发送n个独立位时，信道容量确定为



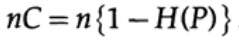
如果我们接近信道的带宽，那么我们应该为每个字符ai发送几乎这样的信息量，i = 1，...，M。假设每个字符ai的出现概率为1 / M，我们得到



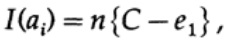
当我们发送M个等概率消息ai中的任何一个时，



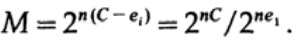
当发送n位时，我们期望发生nQ错误。 实际上，对于包含n位的消息，接收到的消息中大约有nQ个错误。 对于较大的n，相对变化（变化=分布宽度，）
随着n的增加，错误数量的分布将变窄。

因此，从发射器的侧面，我接收ai消息以发送并在其周围绘制半径为球形的球体。



它比误差的预期数量Q略大等于e2（图13.II）。 如果n足够大，则在接收方出现消息点bj的可能性很小，超过该范围。 从发射机的角度来看，我们将得出这种情况：从发送的消息ai到接收的消息bj的任何半径，其错误概率等于（或几乎等于）正态分布，在nQ中达到最大值。 对于任何给定的e2，n都很大，以至于超出我的球体的结果点bj的概率将尽可能小。

现在考虑您的相同情况（图13.III）。 在接收方，在n维空间中围绕接收点bj有一个半径r相同的球体S（r），这样，如果接收到的消息bj在我的球体内，则我发送的消息ai在您的球体内。

如何发生错误？ 下表描述的情况下可能会发生错误：



图13.III



在这里我们可以看到，如果在接收点周围构造的球体中，至少还有一个点对应于可能发送的未编码消息，那么在传输过程中会发生错误，因为您无法确定这些消息中的哪一个被发送。 仅当与之对应的点在球体中时，发送的消息才会包含错误，并且此代码中没有其他可能在同一球体中的点。

如果ai被发送，我们有一个关于Re错误概率的数学方程式



我们可以把第二项中的第一个因子扔掉，取为1。这样，我们得到了不等式



显然，



因此



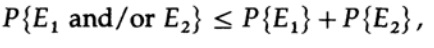
重新申请右边的最后一个成员



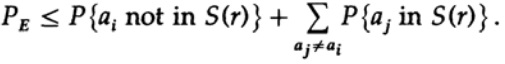
如果将n取足够大，则第一项可以任意取小，例如小于一定数d。 因此，我们有



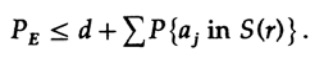
现在，让我们看看如何构建一个简单的替换代码来编码由n位组成的M条消息。 由于不知道如何构建代码（尚未发明纠错码），Shannon选择了随机编码。 为消息中的n位中的每一个翻转硬币，并对M条消息重复该过程。 您需要做的就是抛掷nM个硬币，因此有可能



具有½nM相同概率的代码字典。 当然，创建密码本的随机过程意味着存在重复的可能性，以及代码点彼此接近，因此将成为可能的错误来源。 有必要证明，如果发生这种情况的可能性不大于任何小的选定误差水平，那么给定的n就足够大了。
决定性的一点是，香农将所有可能的代码本平均，以找到平均错误！ 我们将使用Av [。]符号表示所有可能的随机代码字典集中的平均值。 当然，对常数d求平均值当然会得到一个常数，因为求平均值时，每个项与和中的任何其他项都重合



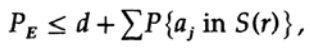
可以增加（M – 1到M）



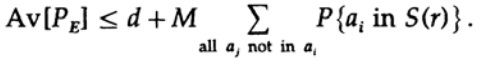
对于任何特定消息，在对所有密码本进行平均时，编码会遍历所有可能的值，因此，点在球体内的平均概率就是球体体积与空间总体积之比。 范围



其中s = Q + e2 <1/2，并且ns必须为整数。

右边的最后一项是这个总和中最大的一项。 首先，我们通过斯特林公式对阶乘进行估算。 然后，我们查看其前面的项的减少系数，请注意，该系数在向左移动时会增加，因此我们可以：（1）将总和的值限制为具有该初始系数的几何级数之和，（2）将几何级数从ns成员扩展为无限数量的项，（3）计算无限几何级数的和（标准代数，无意义），最后得到极限值（对于足够大的n）：



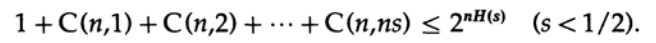
注意熵H（s）如何在二项式恒等式中出现。 请注意，泰勒级数H（s）= H（Q + e2）的展开给出的估计值仅考虑了一阶导数，而忽略了所有其他导数。 现在，让我们收集最终表达式：



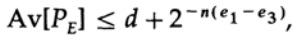
在哪里



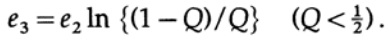
我们需要做的就是选择e2，使e3 <e1，然后最后一项将任意小，因为n足够大。 因此，可以在信道容量任意接近C的情况下任意地获得平均PE误差。
如果所有代码的平均值具有足够小的误差，则至少一个代码必须是合适的，因此，存在至少一个合适的编码系统。 这是香农获得的重要结果-“香农定理用于有干扰的信道”，尽管应该指出的是，他证明了它比我使用的简单二进制对称信道更普遍的情况。 对于一般情况，数学计算要复杂得多，但是思想并没有太大不同，因此，经常使用一个特殊情况的例子可以揭示出该定理的真正含义。

让我们批评一下结果。 我们反复重复：“对于足够大的n。” 但是n有多大？ 非常非常大，如果您真的想同时接近通道的带宽并确保正确的数据传输！ 如此之大，以至于实际上您将不得不等待很长时间才能从这么多的比特中累积一条消息，以便以后对其进行编码。 同时，随机码字典的大小将很大（毕竟，这样的字典不能以比所有Mn位的完整列表短的形式表示，而n和M很大）！

纠错码避免了等待很长的消息，并随后通过非常大的代码簿进行编码和解码，因为纠错码本身就避免了代码簿，而是使用了常规的计算方法。 用简单的理论来说，这样的代码通常会丧失其接近信道容量的能力，同时保持相当低的错误率，但是当代码纠正大量错误时，它们会显示出良好的结果。 换句话说，如果您要为纠错铺设某种通道的容量，那么大多数时候应该使用纠错选项，即每个发送的消息中应修复大量错误，否则您将一无所失。

而且，上面证明的定理仍然不是没有意义的！ 它表明有效的传输系统应针对非常长的位串使用复杂的编码方案。 一个例子是人造卫星飞越了外行星。 当它们远离地球和太阳移动时，它们被迫纠正数据块中越来越多的错误：有些卫星使用的太阳能电池板的功率约为5瓦，而另一些卫星则使用的原子电源功率相同。电源的弱功率，地球上发射器板的尺寸小以及地球上接收器板的尺寸有限，信号必须覆盖的距离太长-所有这些都需要使用具有高级别纠错能力的代码来构建有效的通信系统。

我们返回到上面的证明中使用的n维空间。通过讨论，我们发现球体的几乎整个体积都集中在外表面附近-因此，几乎可以肯定的是，即使该球体的半径较小，发送的信号也将位于围绕接收信号构建的球体表面上。因此，在校正了任意数量的错误nQ之后，接收到的信号变得任意地接近没有错误的信号也就不足为奇了。我们较早检查的通信通道的容量是了解此现象的关键。请注意，为汉明纠错码构造的这种球体不重叠。 n维空间中的大量实际正交测量表明为什么我们可以在一个有微小重叠的空间中拟合M个球体。如果允许一个很小的，任意小的重叠，而这只会导致解码过程中的少量错误，那么您可以在空间中获得密集的球体排列。 Hamming保证一定水平的纠错，Shannon-发生错误的可能性很小，但是同时将实际带宽任意地保持为接近于通信信道的容量，而Hamming代码无法做到这一点。但是，与此同时，实际吞吐量的保持却任意接近通信信道的容量，而汉明码无法做到这一点。但是，与此同时，实际吞吐量的保持却任意接近通信信道的容量，而汉明码无法做到这一点。

信息论并未谈论如何设计有效的系统，但它指出了朝着有效的通信系统发展的方向。这是用于在机器之间建立通信系统的有价值的工具，但是，如前所述，它与人们之间如何交换信息没有太大关系。生物遗传与技术交流系统的相似程度尚不清楚，因此目前尚不清楚信息论如何应用于基因。我们别无选择，只能尝试一下，如果成功向我们展示了这种现象的机器性质，那么失败将指向信息性质的其他重要方面。

让我们不要分心。我们已经看到，所有的初始定义或多或少都应该表达我们最初的信念的本质，但是它们的特征在于一定程度的扭曲，因此不适用。传统上，我们最终使用的定义实际上定义了本质。但是，它仅告诉我们如何处理事物，绝不会使我们有任何意义。在数学界广受赞誉的推定方法在实践中有很多需要改进的地方。

现在，我们来看一个IQ测试的示例，该示例的定义是周期性的，因此会误导您。将创建一个应该用来测量智能的测试。之后，对其进行检查以使其尽可能一致，然后以一种简单的方式对其进行发布和校准，以使所测得的“智能”呈正态分布（当然，沿校准曲线）。所有定义不仅应在首次提出时进行交叉检查，而且在以后的结论中使用时应进行交叉检查。定义界限在多大程度上适合手头的任务？在相同条件下给出的定义多久开始在完全不同的条件下应用？这很常见！在您生命中不可避免地遇到的人文学科中，这种情况经常发生。

因此，除了展示其有用性之外，本信息理论演示的目标之一是警告您这种危险，或演示如何使用它来获得理想的结果。长期以来，人们一直注意到初始定义最终决定了您所找到的内容，其范围比看起来要大得多。最初的定义不仅要求您在任何新情况下，而且在您从事长期工作的领域中都应格外注意。这将使您了解所获得的结果在多大程度上是重言式，而不是有用的。

, . , , , ! , .

...

, — magisterludi2016@yandex.ru

, — «The Dream Machine: » )

, , . ( 10 , 20 )