基本数据结构。 物资。 基础知识

我越来越多地注意到，现代自学成才的人确实缺乏物资。 每个人都懂语言，但是很少了解诸如数据类型或算法之类的基础知识。 有关数据类型的一些知识。

早在1976年，瑞士科学家尼克劳斯·沃思 （ Nicklaus Wirth）撰写了《 算法+数据结构=程序 》一书。

40多年后，这个等式仍然成立。 而且，如果您是一个自学成才的人，并且在编程上花了很长时间研究了这篇文章，那么您可以做对角线。 您可以编写咖啡代码。



本文还将有您可以在面试中听到的问题。

什么是数据结构？

数据结构是一种以特定布局存储数据的容器。 这种“布局”使数据结构在某些操作中有效，而在另一些操作中无效。

哪有

线性元素构成一个序列或线性列表，旁路节点是线性的。 示例：数组。 链表，堆栈和队列。

非线性 ，如果节点的旁路是非线性的，并且数据不一致。 示例：图和树。

基本数据结构。

1. 数组
2. 堆栈
3. Queue列
4. 相关清单
5. 计数
6. 树木
7. 前缀树
8. 表哈希

数组

数组是最简单，使用最广泛的数据结构。 其他数据结构（例如堆栈和队列）是从数组派生的。

大小为4的简单数组的图像，其中包含元素（1、2、3和4）。



每个数据项都被分配一个正数值（索引），它对应于该项在数组中的位置。 大多数语言将数组的起始索引定义为0。

有

一维 ，如上所示。
数组内的多维数组。

基本操作

• 在给定索引处插入-插入元素
• Get-返回给定索引处的元素
• 删除-删除给定索引的项目
• 大小-获取数组中元素的总数

问题

• 找到第二个最小数组元素
• 数组中的第一个非重复整数
• 合并两个排序的数组
• 重新排列数组中的正值和负值

堆栈

堆栈是一种抽象的数据类型，它是根据LIFO原则组织的元素列表（后进先出，后进先出）。

这些不是数组。 到了。 由Alan Thuring发明。

一堆书的示例是一堆垂直排列的书。 为了获得位于中间位置的书，您需要删除放置在书上的所有书。 这就是LIFO（后进先出）方法的工作方式。 应用程序中的“取消”功能可在LIFO上使用。

堆栈图像，分为三个元素（1、2和3），其中3位于顶部，将首先删除。

基本操作

• 推在顶部插入一个项目
• 从堆栈中移除后，弹出返回顶部元素
• isEmpty-如果堆栈为空，则返回true
• 返回顶部元素，而不从堆栈中删除

问题

• 使用堆栈实现队列
• 在堆栈上对值排序
• 在数组中实现两个堆栈
• 使用堆栈反转字符串

Queue列

像堆栈一样，队列以顺序方式存储元素。 与堆栈的显着区别是使用FIFO（先进先出）而不是LIFO。

一条线的一个例子是一行人。 后者拿走了最后一个，而你会，而第一个将离开她的第一个。

队列的图像，包含四个元素（1、2、3和4），其中1位于顶部，将首先删除

基本操作

• 排队-）-在队列末尾插入一个元素
• 出队（）-从队列的开头删除元素
• isEmpty（）-如果队列为空，则返回true
• Top（）-返回队列的第一个元素

问题

• 使用队列实现堆栈
• 反转队列的前N个元素
• 使用队列生成从1到N的二进制数

链表

链表是一个数组，其中每个元素都是一个单独的对象，并且由两个元素组成-数据和到下一个节点的链接。

数组上的主要优点是结构灵活性：链表的元素顺序可能与计算机内存中数据元素位置的顺序不一致，并且遍历列表的顺序始终由其内部关系明确确定。

有

单向 ，每个节点将地址或链接存储到列表中的下一个节点，而最后一个节点的下一个地址或链接为NULL。

1-> 2-> 3-> 4->空

双向 ，与每个节点关联的两个链接，其中一个要点指向下一个节点，一个要点指向上一个节点。

空<-1 <-> 2 <-> 3->空

圆形 ，所有节点都连接成一个圆。 最后没有NULL。 循环链表可以是单或双循环链表。

1-> 2-> 3-> 1

最常见的线性单向列表。 一个示例是文件系统。

基本操作

• InsertAtEnd-将指定的项目插入列表的末尾。
• InsertAtHead-将项目插入列表的顶部
• 删除-从列表中删除指定的项目。
• DeleteAtHead-删除列表的第一个元素
• 搜索-从列表中返回指定的项目
• isEmpty-如果链接列表为空，则返回True

问题

• 链表反向
• 在链表中定义循环
• 从链接列表的末尾返回N个项目
• 从链接列表中删除重复项

计数

图是一组节点（顶点），它们通过边（弧）以网络的形式相互连接。

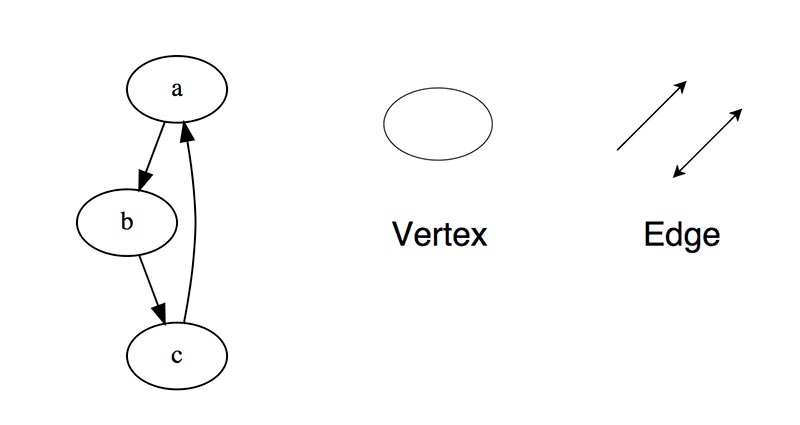
有

定向 ，肋是定向的，即 在两个相连的顶点之间只有一个可用方向。
无方向性的 ，您可以向两个方向的每个肋骨移动。
混合的

发现形式如下

• 邻接矩阵
• 邻接表

通用图遍历算法

• 宽度搜索-级别爬网
• 深度搜索-穿越峰

问题

• 进行宽度和深度搜索
• 检查图是否为树
• 计算图中的边数
• 查找两个峰之间的最短路径

树木

树是由节点（顶点）和边（弧）组成的分层数据结构。 树本质上是没有循环的连接图。

到处都是树结构。 每个人都知道游戏中的技能树。

简单的树



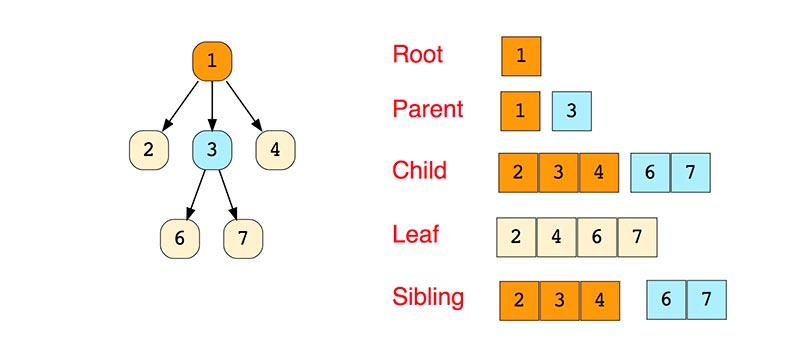
树类型

• N树
• 平衡树
• 二叉树
• 二进制搜索树
• Avl树
• 2-3-4棵树

二叉树是最常见的。

“二叉树是一种分层数据结构，其中每个节点都有一个值（在这种情况下，它也是键），并引用左右后代。 »-产品

绕树的三种方法

• 以直接顺序（从上到下）-前缀形式。
• 以对称顺序（从左到右）-缀形式。
• 以相反的顺序（从下到上）-后缀形式。

问题

• 查找二叉树的高度
• 在二叉搜索树中找到N个最小的项
• 查找距根距离N的节点
• 在二叉树中找到N节点的祖先

特里（前缀树）

一种用于字符串的树，可以快速搜索。 辞典 T9

这样的树就是这样存储单词“ top”，“ thus”和“ their”的。



单词从上到下存储，绿色的节点“ p”，“ s”和“ r”分别指向“ top”，“ thus”和“ their”的末尾。

问题

• 计算总字数
• 打印所有单词
• 从前缀树对数组元素排序
• 创建T9字典

表哈希

散列是用于唯一标识对象并将每个对象存储在预先计算的唯一索引（键）中的过程。

对象存储为键值对，此类元素的集合称为字典。 可以使用此键找到每个对象。

本质上，这是一个将键表示为哈希函数的数组。

散列性能取决于

• 哈希函数
• 哈希表大小
• 碰撞管理方法

数组中哈希匹配的示例。 该数组的索引是通过哈希函数计算的。

问题

• 在数组中查找对称对
• 查找一个数组是否是另一个数组的子集
• 描述开放式哈希

资源清单

• medium.freecodecamp.org/您应该了解自己的下一个编码采访-36af0831f5e3的顶级数据结构
• www.geeksforgeeks.org/commonly-asked-data-structure-interview-questions-set-1
• prog-cpp.ru/数据列表
• habr.com/post/267855
• habr.com/post/273687
• habr.com/post/150732
• ruhighload.com/%D0%A7%D1%82%D0%BE+%D1%82%D0%B0%D0%BA%D0%BE%D0%B5+%D1%85%D0%B5%D1%88-% D1％82％D0％B0％D0％B1％D0％BB％D0％B8％D1％86％D1％8B +％D0％B8 +％D0％BA％D0％B0％D0％BA +％D0％BE％D0％ BD％D0％B8 +％D1％80％D0％B0％D0％B1％D0％BE％D1％82％D0％B0％D1％8E％D1％82
• ru.wikipedia.org

而不是结论

材料与语言本身一样有趣。 也许有人会看到他熟悉并感兴趣的基本结构。

感谢您的阅读。 我希望不要浪费时间=）

PS：事实证明，我很抱歉，文章的翻译已经在这里，而最近，我却忽略了。
如果有兴趣， 她在这里 ，谢谢Hokum ，我会更加小心。