隐藏而不隐藏。 再说一次LSB隐写术，卡方和...奇点？

今天，我们将再次打开旧的巢穴，并讨论如何用猫来隐藏图片中的一堆碎片，研究几种可用的工具并分析最受欢迎的攻击。 看起来，奇异性与它有什么关系？

就像他们说的那样，如果您想弄点什么，那就在Habr上写一篇有关它的文章！ （警告，很多文字和图片）



隐写术 （字面意思是希腊语“密码学”）是一种在其他开放数据（隐身容器）中传输隐藏数据（隐密消息）同时隐藏数据传输事实的科学。 不要惊慌，其实一切都不是那么复杂。

因此，您可以在图像中的什么地方隐藏消息，以便没人注意？

而且只有两个地方：元数据和图像本身。 后者非常简单，只需在Google上键入“ exif”即可 。 因此，让我们立即开始第二个。

最低有效位

最受欢迎的颜色模型是RGB，其中颜色以三个分量的形式表示： 红色，绿色和蓝色 。 每个分量在经典版本中都使用8位编码，也就是说，它的取值可以从0开始
到255。最低有效位在这里隐藏。 重要的是要了解一种这样的RGB颜色占了三个这样的位。

为了更清楚地展示它们，我们将做一些小操作。

按照承诺，以png格式拍摄一只猫的照片。



我们将其分为三个通道，在每个通道中，我们占用最低有效位。 创建三个新图像，每个像素代表NZB。 零-像素为白色，单位分别为黑色。

我们得到这个。




但是，通常，图像以“组合形式”找到。 要在一个图像中表示三个分量的NZB，只需将像素替换为NZB为1的像素，然后将其替换为255，否则将其替换为0就足够了。

但同样重要

想象一下，我们在上一张图中看到的所有内容都是我们的，我们有权对此进行任何操作。 然后，我们将其视为比特流，从这里可以读取和可以写入。

我们获取我们想要散布在图像中的数据，以位的形式呈现它们，并写下它们以代替现有的那些。

为了提取此数据，我们将NZB读取为比特流，并将其转换为所需的形式。 为了找出需要计数的位数，通常将消息大小写到开头。 但是这些是实现细节。

应该注意的是，在大约50％的情况下，我们要写入的位和图片中的位将重合，并且我们无需进行任何更改。

就是这样，方法到此结束。

为什么行得通？

看一下下面的图片。

这是一个空的隐身容器：



这是95％的容量：



看到区别了吗？ 但是她是。 为什么这样

让我们看一下两种颜色：（0，0，0）和（1，1，1），即每个组件中的NZB仅具有不同的颜色。



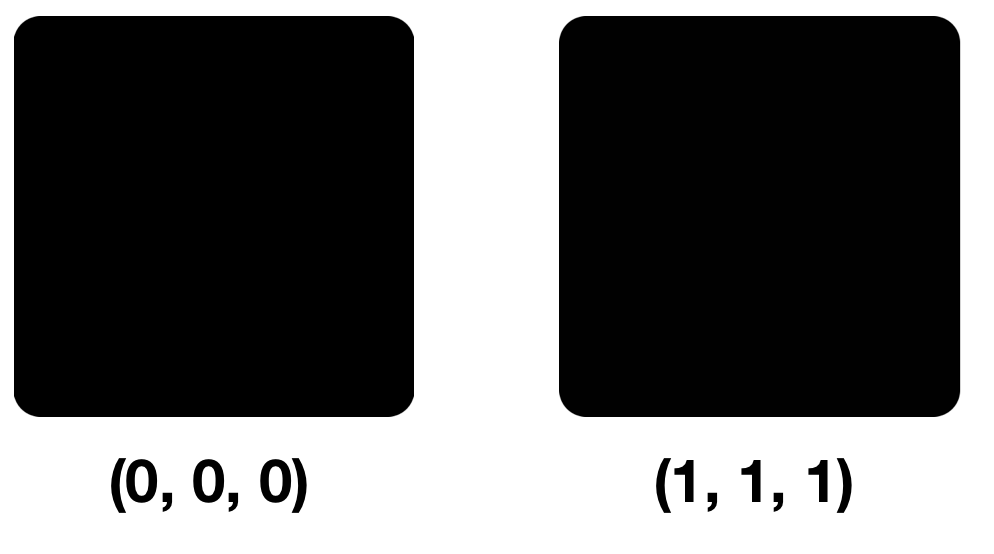
第一，第二和第三眼的像素略有差异将不会引起注意。 事实是，我们的眼睛可以分辨出大约一千万种颜色，而大脑只能分辨出150种颜色。RGB模型还包含16,777,216种颜色。 您可以在此处尝试区分它们。

从命令行

没有很多可用的表示LSB隐写术的开源命令行工具。

最受欢迎的可以在下表中找到。

猫在哪里？

LSB隐写攻击列表中的第一个是视觉攻击。 听起来很奇怪，不是吗？ 毕竟，乍一看，有秘密的猫并没有出卖自己作为装满食物的隐身容器。 嗯...您只需要知道在哪里看。 不难猜测，只有NZB值得我们密切关注。

对于已填充的隐蔽式集装箱，带有NZB的图像如下所示：



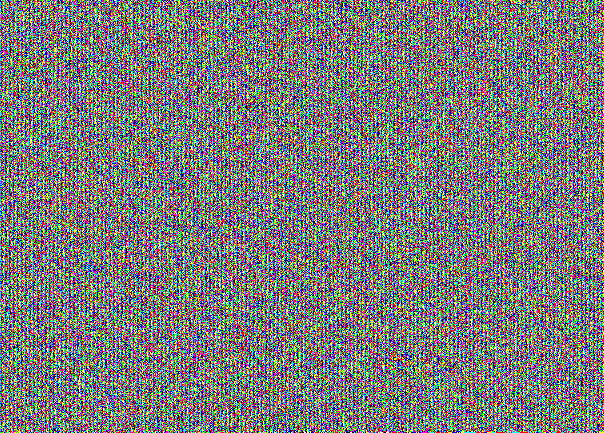
不信？ 在这里，您可以从所有三个渠道分别获得NZB：




这是特定于在NZB中隐藏邮件的“绘图”。 乍一看，这似乎是一种简单的声音。 但是在考虑结构时是可见的。 在这里您可以看到stegocontainer已满。 如果我们以一只可怜的猫的30％的容量接收消息，则会得到以下图片：


他的NZB：



约70％的猫保持不变。

在这里值得做一个小的题外话并讨论大小。 什么是30％的猫？ 猫的大小为603x433像素。 此大小的30％为78459像素。 每个像素包含3位信息。 总的78459 3 = 235377位或不到30 KB，适合30％的密封。 整个猫大约可以容纳100 KB。 这样的事情。

但是我们在这里为您服务是有原因的。 那么，如何欺骗眼睛呢？
首先想到的是：将信息置入噪音中。 但是它不在那里。 接下来是已填充的隐秘容器及其LSB的片段。



稍加努力，我们仍然可以识别出熟悉的结构。 先生们，不要失去希望！

嘻嘻

您知道很多事情都会破坏统计数据。

更改图片中的某些内容，我们将更改其统计属性。 分析人员找到解决这些更改的方法就足够了。

德累斯顿大学的安德里亚斯·韦斯菲尔德（Andreas Wesfield）和安德里亚斯·普菲茨曼（Andreas Pfitzmann）在他们的著作《密写系统的附件》（Attacks on Steganographic Systems）中可以找到这个很好的旧卡方。

在下文中，我们将讨论在同一色彩平面内或在RGB上下文中的攻击在一个通道上的攻击。 每次攻击的结果可以减少到平均水平，并获得“组合”图像的结果。

因此，卡方攻击基于以下假设：在空的隐身容器中同时出现相邻（与最低有效位不同）颜色（值对）的概率非常小。 确实是，您可以相信。 换句话说，对于一个空容器，两种相邻颜色的像素数量明显不同。 我们需要做的就是计算每种颜色的像素数，并应用几个公式。 实际上，这是使用卡方检验检验假设的一项简单任务。

一点数学？

设h为第i个位置的数组，其中包含所研究图像中第i个颜色的像素数。

然后：

1. 实测色频 $$$i = 2k$ ：
   

   $$

   $$n_k = h [2k]，〜k \ in [0，127];$$
   
   
2. 理论上预期的色频 $$$i = 2k$ ：
   

   $$

   $$n_k ^ * = \ frac {h [2k] + h [2k + 1]} {2}，〜k \ in [0,127];$$
   
   

将其转换为Python将会产生如下内容：

for k in range(0, len(histogram) // 2): expected.append(((histogram[2 * k] + histogram[2 * k + 1]) / 2)) observed.append(histogram[2 * k]) 

直方图是图像中颜色i的像素数， $$$i \ in [0，255]$

自由度数k-1的卡方标准计算如下（k是不同颜色的数目，即256）：

$$

$$\ chi_ {k-1} ^ 2 = \ sum_ {i = 1} ^ {k} \ frac {（n_k-n_k ^ *）^ 2} {n_k ^ *};$$

最后，P是分布的概率 $$$n_i$ 和 $$$n_i ^ *$ 在这些条件下，它们是相等的（我们有一个装满的隐身容器的可能性）。 通过整合平滑度函数来计算：

$$

$$P = 1-\ frac {1} {2 ^ {\ frac {k-1} {2}} \ Gamma（\ frac {k-1} {2}）} \ int_0 ^ {\ chi_ {k-1 } ^ 2} e ^ {-\ frac {x} {2}} x ^ {\ frac {k-1} {2} -1} dx;$$

最有效的方法是，不对整个图像应用卡方，而仅对部分（例如线）应用卡方。 如果计算出的线的概率大于0.5，则用红色填充原始图像中的线。 如果少于，则为绿色。 对于丰满度为30％的猫，图片如下所示：



完全正确，不是吗？

好吧，我们受到了数学上的声音攻击，您不能欺骗数学！ 还是... ??

随机舞

这个想法很简单：不是按顺序写入位，而是在随机位置写入。 为此，您需要使用PRSP，将其配置为发出具有相同边（即密码）的相同随机流。 在不知道密码的情况下，我们将无法配置PRNG并找到隐藏消息的像素。 我们将在猫上对其进行测试。

小猫（完成率32％）：



他的最低位：



图片看起来很吵，但对于没有经验的分析师来说并不令人怀疑。 卡方说什么？


看来黑帽子赢了！ 无论如何...

正则奇异

另一种统计方法是2001年的Jessica Friedrich，Miroslav Golyan和Andreas Pfitzman。 它被称为RS方法。 原始文章可以在这里获取。

该方法包含几个准备步骤。

图像分为n个像素组。 例如，连续4个连续像素。 通常，这些组包含相邻像素。
对于顺序填充红色通道的猫，前五个组将是：

• [78，78，79，78]
  
• [78，78，78，78]
  
• [78，79，78，79]
  
• [79，76，79，76]
  
• [76，76，76，77]
  

（所有测量均为经典版本的RGB）

然后，我们定义了所谓的判别函数或平滑函数，该函数将每组像素映射到一个实数。 此功能的目的是捕获像素组G的平滑度或“规则性”。 $$$G =（x_1，...，x_n）$ ，判别功能将越重要。 通常，选择一组像素的“变化”，或更简单地，选择一组中相邻像素的差异之和。 但它也可以考虑有关图像的统计假设。

$$

$$f（x_1，x_2，...，x_n）= \ sum_ {i = 1} ^ {n-1} | x_ {i + 1}-x_i |$$

示例中一组像素的平滑度函数的值：

• f（78，78，79，78）= 2
• f（78，78，78，78）= 0
• f（78，79，78，79）= 3
• f（79，76，79，76）= 9
• f（76，76，76，77）= 1

接下来，确定来自一个像素的翻转函数的类别。

它们必须具有一些属性。

$$

$$1. ~~~ \ forall x \ in P：〜F（F（x））= x，~~ P = \ {0，〜255 \};$$

$$

$$2. ~~~ F_1：0 \ leftrightarrow 1，1，〜2 \ leftrightarrow 3，〜...，254 \ leftrightarrow 255;$$

$$

哪里 $$$F$ -一类的任何功能， $$$F_1$ 是直接翻转功能，并且 $$$F _ {-1}$ -反向。 另外，通常将相同的翻转功能表示为 $$$F_0$ 不会改变像素。

python翻转功能可能看起来像这样：

 def flip(val): if val & 1: return val - 1 return val + 1 def invert_flip(val): if val & 1: return val + 1 return val - 1 def null_flip(val): return val 

对于每组像素，我们应用一种翻转功能，并根据翻转前后判别函数的值来确定像素组的类型：正常（ R egular），单个/不寻常（Singular）和无用的不可用。 由于后一种类型不再使用，因此该方法以键类型的首字母命名。 这就是名字的全部秘密，奇点与它无关：)



我们可能想对不同的像素应用不同的翻转，为此，我们定义了一个具有N值-1、0或1的蒙版M。

$$

$$F_M（G）=（F_ {M（1）}（x_1），F_ {M（2）}（x_2），...，F_ {M（n）}（x_n））$$

让我们的示例中的掩码为经典-[1、0、0、1]。 通过实验发现，不包含 $$$F _ {-1}$ 。 成功的选项还有：[0，1，0，1]，[0，1，1，0]，[1，0，1，0]。 我们对示例中的组应用翻转，计算平滑度值并确定像素组的类型：

• $$$F_m$ （78，78，79，78）= [79，78，79，79];
  f（79，78，79，79）= 2 = 2 = f（78，78，79，78）
  无法使用的群组
  
  
• $$$F_m$ （78，78，78，78）= [79，78，78，79];
  f（79，78，78，79）= 2> 0 = f（78，78，78，78）
  常规组
  
  
• $$$F_m$ （78，79，78，79）= [79，79，78，78];
  f（79，79，78，78）= 1 <3 = f（78，79，78，79）单数组
  
  
• $$$F_m$ （79，76，79，76）= [78，76，79，77];
  f（78，76，79，77）= 7 <9 = f（79，76，79，76）单数组
  
  
• $$$F_m$ （76，76，76，77）= [77，76，76，76];
  f（77，76，76，76）= 1 = 1 = f（76，76，76，77）
  无法使用的群组
  
  

我们将掩码M的常规组数表示为 $$$R_M$ （以所有组的百分比表示），以及 $$$S_M$ 对于单个群体。

然后 $$$R_M + S_M \ leq 1$ 和 $$$R _ {-M} + S _ {-M} \ leq 1$ ，对于负遮罩（所有遮罩分量乘以-1），因为 $$$R_M + S_M + U_M = 1$ 一会儿 $$$U_M$ 可能是空的。 对于负遮罩也是如此。

主要的统计假设是，在典型图像中，期望值 $$$R_M$ 等于 $$$R _ {-M}$ ，对于 $$$S_M$ 和 $$$S _ {-M}$ 。 实验数据和一些手鼓围绕翻转功能的最后特性证明了这一点。

$$

$$R_M \ cong S_M ~~~~ R _ {-M} \ cong S _ {-M}$$

我们来看一个小例子吗？ 鉴于样本量较小，我们可能无法证实这一假设。 让我们看看反转蒙版会发生什么：[-1，0，0，-1]。

• F_M（78，78，79，78）= [77，78，79，77];
  f（77，78，79，77）= 4> 2 = f（77，78，79，77）
  常规组
  
  
• F_M（78，78，78，78）= [77，78，78，77];
  f（77，78，78，77）= 2> 0 = f（78，78，78，78）
  常规组
  
  
• F_M（78，79，78，79）= [77，79，78，80];
  f（77，79，78，80）= 5> 3 = f（78，79，78，79）
  常规组
  
  
• F_M（79，76，79，76）= [80，76，79，75];
  f（80，76，79，75）= 11> 9 = f（79，76，79，76）
  常规组
  
  
• F_M（76，76，76，77）= [75，76，76，78];
  f（75，76，76，78）= 3> 1 = f（76，76，76，77）
  常规组
  
  

好吧，一切都是显而易见的。

但是之间的区别 $$$R_M$ 和 $$$S_M$ 随着嵌入消息的长度m的增加，趋向于零，我们得到 $$$R_M \ cong S_M$ 。

有趣的是，LSB平面的随机化对 $$$R _ {-M}$ 和 $$$S _ {-M}$ 。 它们的差异随着嵌入消息的长度m而增加。 可以在原始文章中找到对此现象的解释。

这是时间表 $$$R_M$ ， $$$S_M$ ， $$$R _ {-M}$ 和 $$$S _ {-M}$ 取决于具有倒置LSB的像素数，它称为RS图。 x轴是具有倒置LSB的像素的百分比，y轴是具有蒙版M和-M的规则和奇异组的相对数量， $$$M = [0〜1〜1〜0]$ 。



RS隐写分析方法的本质是评估RS图的四条曲线并使用外推法计算它们的交点。 假设我们有一个隐身容器，其消息的未知长度为p（以像素的百分比表示）嵌入在随机选择的像素的较低位中（即使用RandomLSB）。 我们对R和S组数的初始测量对应于点 $$$R_M（p / 2）$ ， $$$S_M（p / 2）$ ， $$$R _ {-M}（p / 2）$ 和 $$$S _ {-M}（p / 2）$ 。 由于消息是随机的位流，因此我们从消息长度的一半恰好取点，并且如前所述，平均而言，通过嵌入消息，只有一半的像素会发生变化。

如果我们反转图像中所有像素的LSB并计算R和S组的数量，我们将得到四个点 $$$R_M（1-p / 2）$ ， $$$S_M（1-p / 2）$ ， $$$R _ {-M}（1-p / 2）$ 和 $$$S _ {-M}（1-p / 2）$ 。 由于这两点取决于LSB的特定随机性，因此我们必须重复此过程多次并评估 $$$R_M（1/2）$ 和 $$$S_M（1/2）$ 来自统计样本。

我们可以有条件地通过点画线 $$$R _ {-M}（p / 2）$ ， $$$R _ {-M}（1-p / 2）$ 和 $$$S _ {-M}（p / 2）$ ， $$$S _ {-M}（1-p / 2）$ 。

点数 $$$R_M（p / 2）$ ， $$$R_M（1/2）$ ， $$$R_M（1-p / 2）$ 和 $$$S_M（p / 2）$ ， $$$S_M（1/2）$ ， $$$S_M（1-p / 2）$ 定义两个抛物线。 每个抛物线和相应的线在左侧相交。 两个交点的x坐标的算术平均值使我们能够估计未知消息的长度p。

为了避免对中点RM（1/2）和SM（1/2）进行长时间的统计估计，可以考虑以下两个方面：

1. 曲线交点 $$$R_M$ 和 $$$R _ {-M}$ 与曲线的交点具有相同的x坐标 $$$S_M$ 和 $$$S _ {-M}$ 。 这实质上是我们的统计假设的更严格版本。 （见上文）
2. RM和SM曲线在m = 50％处相交，或者 $$$R_M（1/2）= S_M（1/2）$ 。

这两个假设为秘密消息p的长度提供了一个简单的公式。 缩放x轴以使p / 2变为0且1-p / 2变为1之后，交点的x坐标是以下二次方程式的根



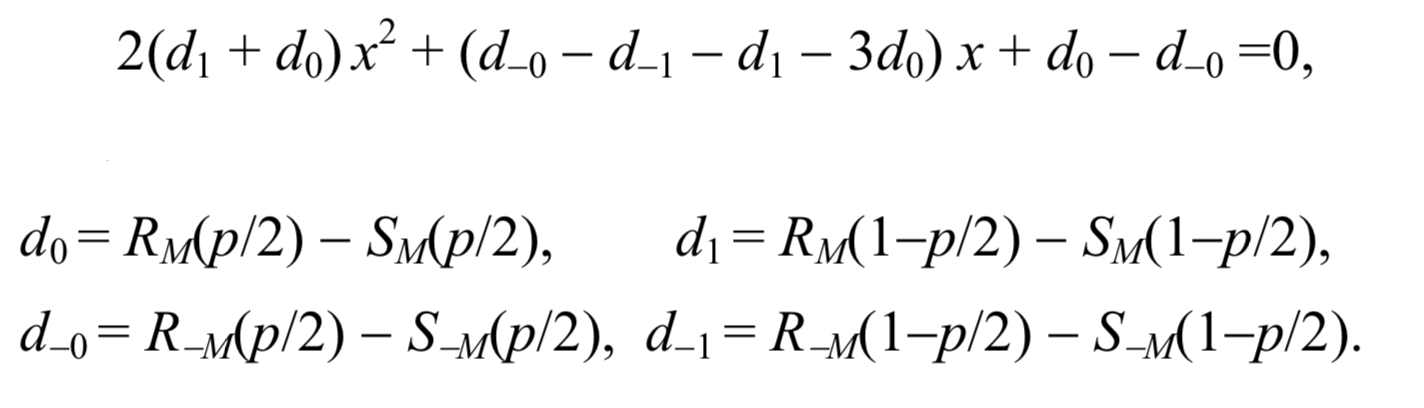
然后可以通过以下公式计算邮件长度：

$$

$$p = \ frac {x} {x- \ frac {1} {2}}$$

在这里，我们的猫进入了场景。 （不是时候给他起个名字吗？）

因此，我们有：

• 常规RM组（p / 2）：23121个
• 单个SM组（p / 2）：14124个
• 带有反面罩RM的常规组（p / 2）：37191个
• 带反光罩SM（p / 2）的单组：8440个。
• 倒LSB RM（1-p / 2）的常规组：20298个
• 具有反向LSB SM（1-p / 2）的单组：16206个。
• 带有反向LSB和反向掩膜RM（1-p / 2）的常规组：40603个。
• 具有倒置LSB和倒置蒙版SM（1-p / 2）的单组：6947个。

（如果您有很多空闲时间，则可以自己计算，但是现在我建议您相信我的计算）

在议程上，我们只剩下一个简单的数学。 还记得如何求解二次方程吗？

$$

$$d_0 = 8997$$

$$

$$d _ {-0} = $ 2875$$

$$

$$d_1 = 4092$$

$$

$$d _ {-1} = 33656$$

将所有d代入上述公式，我们得到一个二次方程式，可以根据学校的教学方法求解。

$$

$$26178x ^ 2-35988x-19754 = 0$$

$$

$$D =（-35988）^ 2-426178 *（-19754）= $ 336361699$$

$$

$$x_1 = 1.7951 ~~~~~~~~ x_2 = -0.4204$$

取较小的模数根，即 $$$x_2$ 。 那么，内置在猫中的消息的近似估计将是：

$$

$$p = \ frac {-0.4204} {-0.4204-0.5} = 0.4567$$

是的，此方法有一个大加号和一个大减号。 优点是该方法可用于普通LSB隐写术和RandomLSB隐写术。 卡方不能吹嘘这种机会。 该方法可以准确识别我们看似随机的猫，并估计消息长度为0.3256，这非常非常准确。

负号在于此方法的大（非常大）误差，该误差随着带有顺序嵌入的长消息一起增长。 例如，对于占用率为30％的猫，我对方法的实现方式给出了三个通道的近似平均估计值，即0.4633或总容量的46％，占用率超过95％-0.8597。 但对于一只空猫，则高达0.0054。 这是独立于实施的总体趋势。 普通LSB方法的最精确结果给出了10％+-5％的内置消息长度。

正负

为了不被抓住，必须一定是意外的，并使用±1编码。 而不是更改颜色字节中的最低有效位，我们将整个字节增加或减少一个。 只有两个例外：

• 我们不能减少零，因此我们会增加它，
  
• 我们也不能增加255，因此我们将始终减小该值。
  

对于所有其他字节值，我们完全随机选择增加一个或减少一个。 除此操作外，LSB将像以前一样进行更改。 为了提高可靠性，最好采用随机字节来记录消息。

这是我们的朋友猫：



从外部看，由于不可见（0，0，0）和（1、1，1）之间的差异的相同原因，引言是完全不可察觉的。



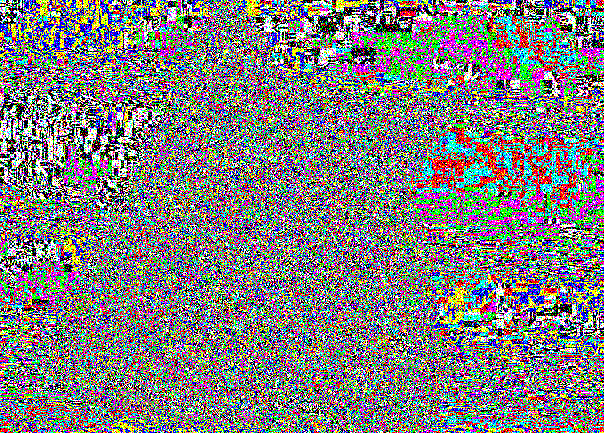
由于在随机位置记录，因此LSB片段仅保持嘈杂。



卡方仍然是盲点，RS方法给出的概算为0.0036 。

不太高兴，请在此处阅读此文章。

最细心的人可能会问，如果随机更改整个字节，并且没有用于设置PRNG的密码（最好使用不同的种子，也就是生成器的状态，也可以使用密码来处理RandomLSB和±1编码），如何获取消息。 答案越简单越好。 我们获得消息的方式与没有±1编码的方式相同。 我们甚至可能不知道它的用途。 我再说一遍，我们仅使用此技巧绕过自动检测工具 。 嵌入/检索邮件时，我们仅使用其LSB，仅此而已。 但是，在检测时，我们需要考虑实现上下文，即图像的所有字节，以便建立统计估计。 这恰恰是±1编码的全部成功。

而不是结论

另一种非常好的尝试是使用针对LSB隐写的统计数据，该方法称为“样本对”。 您可以在这里找到它。 他的到来会使这篇文章过于学术化，因此我对课外阅读感兴趣。 但是，在预见到观众的问题后，我会立即回答：不，他没有掌握±1的编码。

当然还有机器学习。 基于ML的现代方法给出了很好的结果。 您可以在这里和这里阅读有关它的信息 。

基于本文，编写了一个小工具 （目前）。 它可以生成数据，分别在通道上进行视觉攻击，计算RS，SPA评估并可视化卡方的结果。 而且她不会停在那里。

总结一下，我想给出一些提示：

• 将消息嵌入随机字节中。
• 尽可能减少嵌入的信息量（记住汉明大叔）。
• 使用±1编码。
• 选择嘈杂的LSB图片。
• Remdalp的 UPD：使用不会在任何地方出现的图像。
• 乖！

我很高兴看到您的建议，补充，更正和其他反馈！

PS我要特别感谢PavelMSTU的咨询和激励。