🥪 🆓 🌟 神经网络ALU的简单介绍：解释，物理含义和实现 🔏 🌤️ 🕛

最近，安德鲁·特拉斯克（Andrew Trask）的Google DeepMind研究人员（包括著名的人工智能科学家，《理解深度学习》一书的作者）发表了一篇令人印象深刻的文章，描述了一种神经网络模型，该模型可以高精度地外推简单和复杂的数值函数的值。

在这篇文章中，我将解释NALU （神经算术逻辑设备，NALU）的体系结构，其组成部分以及与传统神经网络的显着区别。本文的主要目的是为神经网络和深度学习的新手科学家，程序员和学生简单直观地解释NALU （实现和思想）。

作者注 ：我也强烈建议阅读原始文章，以更详细地研究该主题。

神经网络什么时候出错？

图片摘自本文。

从理论上讲，神经网络应该很好地近似函数。他们几乎总是能够识别输入数据（因子或特征）与输出（标签或目标）之间的重要对应关系。这就是为什么神经网络被用于许多领域，从对象识别及其分类到将语音转换为文本以及实施能够击败世界冠军的游戏算法。已经创建了许多不同的模型：卷积神经网络和递归神经网络，自动编码器等。成功创建神经网络和深度学习的新模型本身就是一个大话题。

但是，根据本文的作者所说，神经网络并不总是能应付似乎对人甚至蜜蜂都显而易见的任务！例如，这是一个具有数字的口头帐户或操作，以及从关系中识别依赖关系的能力。文章显示，神经网络的标准模型甚至无法应付相同的映射（将参数转换为自身的函数，

f （ x ） = x

$f（x）= x$ ）是最明显的数值关系。下图显示了学习此函数值时各种神经网络模型的MSE 。

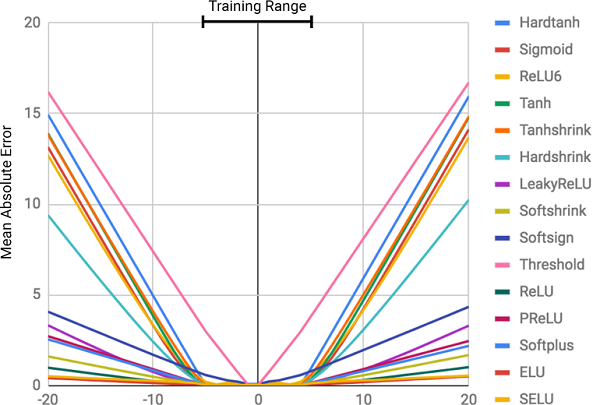该图显示了在内层中使用相同架构和不同（非线性）激活函数的标准神经网络的均方误差

为什么神经网络错了？

从图中可以看出，未命中的主要原因是神经网络内层上激活函数的非线性 。这种方法对于确定输入数据和响应之间的非线性关系非常有用，但是超出网络学习的数据是非常错误的。因此，神经网络在记住训练数据的数值依赖性方面做得很出色，但是他们不能外推。

这就像在考试前塞满答案或主题而不理解主题。如果问题类似于家庭作业，则很容易通过测试，但是如果是对被测主题的理解而不是记忆能力，我们将失败。

哈利·波特

这不在课程程序中！

误差程度与所选激活函数的非线性程度直接相关。上图清楚地表明，具有硬约束的非线性函数（例如S形或双曲线正切（ Tanh ））可以解决比软约束函数（例如截断的线性变换）更弱的泛化依赖关系的任务。

解决方案：神经电池（NAC）

神经电池（ NAC ）是NALU模型的核心。这是处理加法和减法的神经网络的简单但有效的部分，这对于有效计算线性关系是必需的。

NAC是神经网络的一个特殊线性层，在其上施加了简单的条件权重：它们只能采用3个值-1、0或-1 。这种限制不允许电池改变输入数据的范围，并且在网络的所有层上都保持不变，无论其数量和连接如何。因此，输出是输入向量值的线性组合 ，可以很容易地进行加法和减法运算。

大声的想法 ：为了更好地理解该语句，让我们看一个构造神经网络层的示例，该层对输入数据执行线性算术运算。

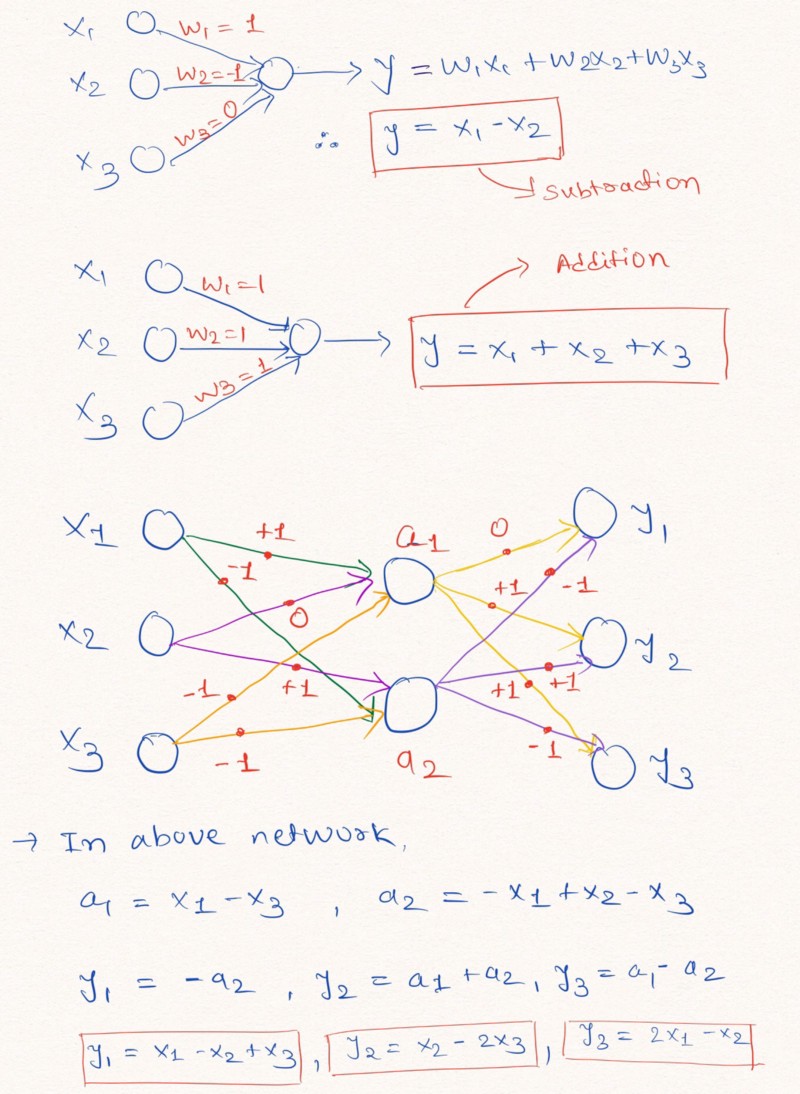神经网络中的线性外推

该图说明了不添加常数且权重值为-1、0或1的神经网络各层如何执行线性外推

如上图所示，神经网络可以学习外推诸如加法和减法（

y = x_{1} + x_{2}

$y = x_1 + x_2$ 和

y = x_{1} - x_{2}

$y = x_1-x_2$ ），使用权重限制（可能值为1、0和-1）。

注意：在这种情况下，NAC层不包含自由项（常数），并且不对数据应用非线性变换。

由于标准神经网络无法在相似的限制下解决问题，因此本文的作者提供了一个非常有用的公式，用于通过经典（无限）参数来计算此类参数

\帽 子 W

$\帽子{W}$ 和

\帽 子 M

$\帽子{M}$ 。像神经网络的所有参数一样，权重数据可以在训练网络的过程中随机初始化和选择。向量计算公式

W

$W$ 通过

\帽 子 W

$\帽子{W}$ 和

\帽 子 M

$\帽子{M}$ 看起来像这样：

W = t a n h （ h a t W ） o d o t s i g m a （ h a t M ）

$W = tanh（\ hat {W}）\ odot \ sigma（\ hat {M}）$

该公式使用逐元素矩阵积

使用该公式可确保 W值的范围为[-1，1]，该范围更接近设置-1，0，1。此外，该方程式的函数可以通过权重参数进行微分。因此，我们的NAC层将更容易学习价值

W

$W$ 使用梯度下降和误差的反向传播 。以下是NAC层的体系结构图。

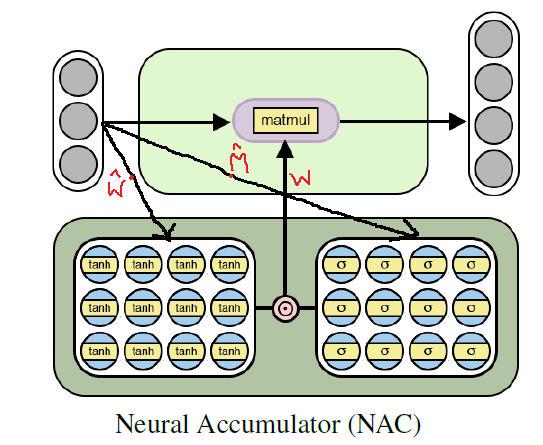神经电池架构

用于训练基本（线性）算术函数的神经电池的体系结构

使用Tensorflow实现Python NAC

正如我们已经了解的那样， NAC是一个具有小功能的相当简单的神经网络（网络层）。以下是使用Tensoflow和NumPy库在Python中实现单个NAC层的实现。

Python代码

import numpy as np import tensorflow as tf #    (NAC)  / # ->     / def nac_simple_single_layer(x_in, out_units): '''  : x_in ->   X out_units ->     : y_out ->     W ->     ''' #       in_features = x_in.shape[1] #  W_hat  M_hat W_hat = tf.get_variable(shape=[in_shape, out_units], initializer=tf.initializers.random_uniform(minval=-2, maxval=2), trainable=True, name='W_hat') M_hat = tf.get_variable(shape=[in_shape, out_units], initializer=tf.initializers.random_uniform(minval=-2, maxval=2), trainable=True, name='M_hat') #  W   W = tf.nn.tanh(W_hat) * tf.nn.sigmoid(M_hat) y_out = tf.matmul(x_in, W) return y_out, W

在上面的代码中

\帽 子 W

$\帽子{W}$ 和

\帽 子 M

$\帽子{M}$ 可以使用均匀分布进行初始化，但是可以使用任何建议的方法为这些参数生成初始近似值。您可以在我的GitHub存储库中看到代码的完整版本（该链接在文章末尾重复）。

继续：从加减到NAC的复杂算术表达式

尽管上述简单神经网络的模型可以应对最简单的操作（例如加法和减法），但是我们需要能够从更复杂的函数（例如乘法，除法和求幂）的许多含义中学习。

下面是经过修改的NAC体系结构，该体系结构适用于通过对数并采用模型内的指数来选择更复杂的算术运算 。请注意，此NAC实现与上面已讨论的实现之间的差异。

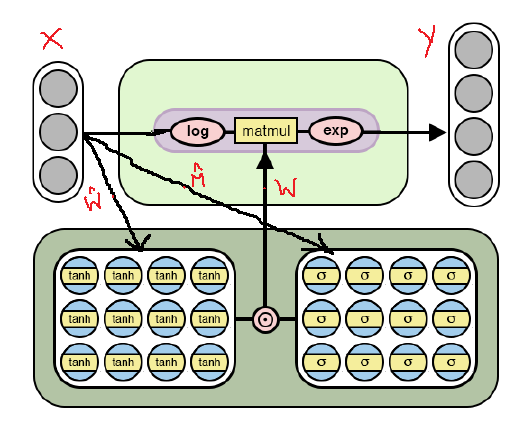NAC体系结构可用于更复杂的算术运算

从图中可以看出，在对输入数据乘以权重矩阵之前，对数进行对数运算，然后计算结果的指数。计算公式如下：

Y = e x p （ W b u l l e t （ l o g （ | x | + e p s i l o n ） ） ）

$Y = exp（W \ bullet（log（| x | + \ epsilon）））$

NAC的第二个版本的输出公式。

$\ epsilon$ 这是一个非常小的数字，以防止在训练期间出现log（0）之类的情况

因此，对于两个NAC模型，其工作原理都包括带有权重的权重矩阵的计算

W

$W$ 通过

\帽 子 W

$\帽子{W}$ 和

\帽 子 M

$\帽子{M}$ 不会改变。唯一的区别是在第二种情况下对输入和输出使用对数运算。

使用Tensorflow的Python中的第二个NAC版本

像体系结构一样，除了在输出值张量的计算中指出的改进之外，该代码几乎不会更改。

Python代码

 #    (NAC)     # ->      ,   ,      def nac_complex_single_layer(x_in, out_units, epsilon=0.000001): ''' :param x_in:   X :param out_units:    :param epsilon:    (,    log(0)   ) :return m:     :return W:     ''' in_features = x_in.shape[1] W_hat = tf.get_variable(shape=[in_shape, out_units], initializer=tf.initializers.random_uniform(minval=-2, maxval=2), trainable=True, name="W_hat") M_hat = tf.get_variable(shape=[in_shape, out_units], initializer=tf.initializers.random_uniform(minval=-2, maxval=2), trainable=True, name="M_hat") #  W   W = tf.nn.tanh(W_hat) * tf.nn.sigmoid(M_hat) #          x_modified = tf.log(tf.abs(x_in) + epsilon) m = tf.exp(tf.matmul(x_modified, W)) return m, W

我再次提醒您，可以在我的GitHub存储库中找到完整版本的代码（该链接在文章末尾重复）。

放在一起：神经算术逻辑单元（NALU）

正如许多人已经猜到的那样，我们可以从几乎所有的算术运算中学习，并结合上面讨论的两个模型。这是NALU的主要思想 ，它包括通过训练信号控制的基本NAC和复杂NAC的加权组合 。因此， NAC是构建NALU的基础，并且，如果您了解它们的设计，则构建NALU将会很容易。如果仍有疑问，请尝试再次阅读两种NAC型号的说明。下面是带有NALU体系结构的图表。

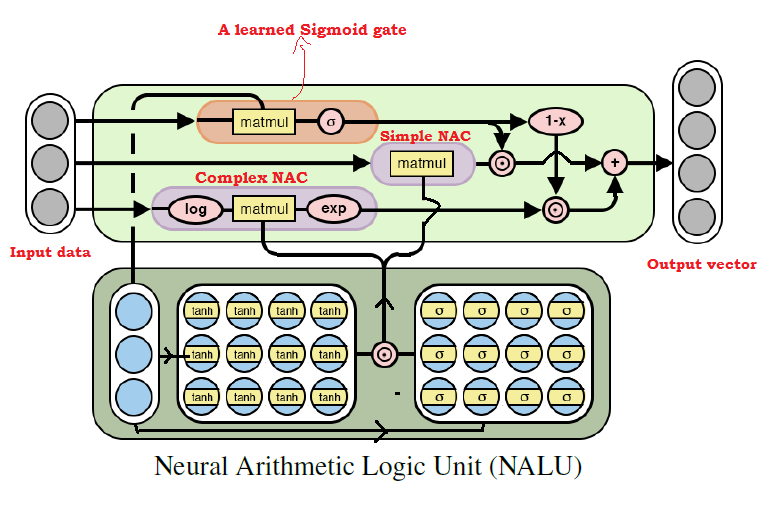NALU体系结构图及其说明

从上图可以看出， NALU内部的两个NAC单元（紫色块）都通过训练信号S型（橙色块）进行插值（组合）。这使您可以（取消）激活其中任何一个的输出，具体取决于算术函数（我们尝试查找其值）。

如上所述， NAC基本单元是一个累加功能，它允许NALU执行基本线性运算（加法和减法），而复数NAC单元负责乘法，除法和乘幂运算。 NALU中 的输出可以表示为以下公式：

伪代码

 Simple NAC : a = WX Complex NAC: m = exp(W log(|X| + e))  W = tanh(W_hat) * sigmoid(M_hat) #  G -       : g = sigmoid(GX) # , ,   NALU #  *      NALU: y = g * a + (1 - g) * m

从上面的NALU公式，我们可以得出结论：

g = 0

$g = 0$ 神经网络将仅选择用于复杂算术运算的值，而不选择用于基本算术运算的值；反之亦然-如果是

g = 1

$g = 1$ 。因此，一般而言， NALU能够学习任何由加，减，乘，除，乘幂运算构成的算术运算，并成功地推断出超出源数据值间隔范围的结果。

使用Tensorflow的Python NALU实现

在NALU的实现中，我们将使用我们已经定义的基本NAC和复杂NAC 。

Python代码

 def nalu(x_in, out_units, epsilon=0.000001, get_weights=False): ''' :param x_in:   X :param out_units:    :param epsilon:    (,    log(0)   ) :param get_weights:   True      :return y_out:     :return G: o   :return W_simple:    NAC1 ( NAC) :return W_complex:    NAC2 ( NAC) ''' in_features = x_in.shape[1] #     NAC a, W_simple = nac_simple_single_layer(x_in, out_units) #     NAC m, W_complex = nac_complex_single_layer(x_in, out_units, epsilon=epsilon) #    G = tf.get_variable(shape=[in_shape, out_units], initializer=tf.random_normal_initializer(stddev=1.0), trainable=True, name="Gate_weights") g = tf.nn.sigmoid(tf.matmul(x_in, G)) y_out = g * a + (1 - g) * m if(get_weights): return y_out, G, W_simple, W_complex else: return y_out

再次注意，在上面的代码中，我再次初始化了参数矩阵

G

$G$ 使用均匀分布，但是您可以使用任何推荐的方法来生成初始近似值。

总结

对我个人而言， NALU的想法是AI领域（尤其是神经网络）的一项重大突破，并且看起来很有希望。这种方法可以为标准神经网络无法应对的应用领域敞开大门。

本文的作者讨论了使用NALU进行的各种实验：从选择基本算术函数的值到对给定的MNIST图像序列中的手写数字进行计数，这使神经网络可以检查计算机程序！

结果令人印象深刻，并证明NALU可以处理几乎所有与数字表示有关的任务，其效果优于神经网络的标准模型。我鼓励读者熟悉实验结果，以便更好地了解NALU模型的使用方式和位置。

但是，必须记住， NAC和NALU都不是任何任务的理想解决方案。相反，它们代表了有关如何为特定类型的算术运算创建模型的一般思想。

下面是指向我的GitHub存储库的链接，其中包含本文代码的完整实现。
github.com/faizan2786/nalu_implementation

您可以通过为神经网络选择超参数来独立检查模型在各种功能上的运行情况。请在本文下方的评论中提出问题并分享您的想法，我将尽力回答您。

PS（来自作者）：这是我有史以来第一篇书面文章，因此，如果您对未来（技术和一般）有任何提示，建议和建议，请给我写信。

PPS（来自翻译者）：如果您对翻译或文字有意见，请给我写一封个人信息。我对学习到的门信号的措词特别感兴趣-我不确定我能否准确翻译这个术语。

神经网络ALU的简单介绍：解释，物理含义和实现

神经网络什么时候出错？

为什么神经网络错了？

解决方案：神经电池（NAC）

使用Tensorflow实现Python NAC

继续：从加减到NAC的复杂算术表达式

使用Tensorflow的Python中的第二个NAC版本

放在一起：神经算术逻辑单元（NALU）

使用Tensorflow的Python NALU实现

总结

More articles: