
我认为,在本文中,我将提供一种有趣的解决方案,无需使用训练即可对图像中的对象进行计算机识别。
任务:拍摄多层建筑物的照片,然后尝试确定其中的楼层数。
对楼层数的一个很好的估算可以得出房屋垂直方向的窗户数。 窗户,阳台和其他物体是地板的良好特征(尤其是在住宅建筑中)。 我将考虑住宅建筑物,这些建筑物的图像很容易在网络上找到。 事先应注意一个重要限制:图像中的房屋必须完全垂直显示,以便可以从视觉上检测所有楼层。
任务合理地分为两个阶段:
- 搜索要计数的窗口的垂直“条”。 两个子任务:首先,您需要在房屋所占据的图像区域中查找窗户;其次,住宅建筑物中有很多窗户,对它们全部进行分析是没有意义的。 有必要在其中突出显示最适合后续分析的垂直序列。
- 通过房屋的选定区域确定楼层(窗户或其他特征对象)的数量。
本文主要致力于解决方案的第一步。 第二步仍在开发中,但我还将给出其解决方案的一些结果。
步骤1.使用Windows搜索区域
基本思想是,在一排相同对象的房屋中可以很好地区分的一系列相同对象(例如窗户)会产生像素亮度的周期性序列。 这正是要找到的顺序。 以下是该算法的主要阶段。
首先,我们将图像转换为灰色阴影并将其缩放(我使用了400x600px的图片)

图1原始黑白图像
进一步循环:
- 在相对较窄(40像素)的条带上选择整个高度的图像(图2,下部图像,不带点)
- 在条带宽度上平均亮度。 得出平均亮度在房屋高度上的分布线w(图2上方的图)。 它具有窗户的区域具有清晰可见的周期性结构特征。 位于阴影处的窗户很难分辨,但这不会造成伤害。
- 计算出偏移了距离sh的w和w的值之差dw。 搜索方法使用这样的偏移值sh来实现差异dw的中值的最大减小(图2,下图)。


图2窗口“条”
但是,仅找到中间值最大程度降低的图像带是不够的。 事实是,具有绿化或天空且剪切值较小的区域会比窗户减少更多。 但是,如果我们绘制带窗和不带窗的带材的中间值对位移值的依赖性,那么我们可以注意到一个关键的区别:对于接近地板高度的位移值,带有窗的图形具有清晰可见的极值。 因此,没有必要测量中位数的绝对达到的水平,而是在增加每个窗口的偏移的过程中,其最大值从最大值中减小。 这是关键。
| 没有窗户 | 带窗户 |
|---|
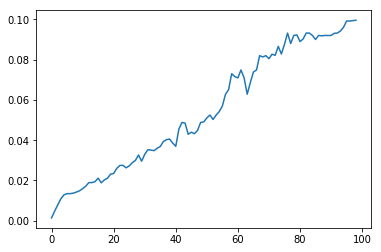 | 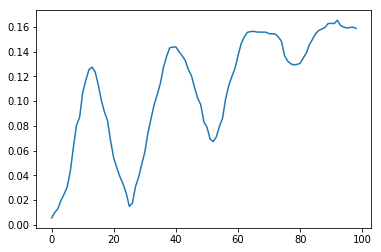 |
图3平均亮度的中位数随偏移的增加而变化
以下是带有注释的python3代码。
image = Image.open("raf_data/32.jpg").resize((600,400)) # . img = np.array(image.convert("L"), dtype=float)/255 SEARCH_WIDTH = 40 # x_opt = [0, 1] # : sh_range = range(1,100) # kmax = 0 # for x in range(0, img.shape[1]-SEARCH_WIDTH, int(SEARCH_WIDTH/2)): amax = 0 amin = 1 # for sh in sh_range: # w = img[:,x:x+SEARCH_WIDTH].mean(axis=1) aim = (pd.DataFrame(w)-pd.DataFrame(w).shift(sh))[sh:].abs().median().values[0] # aim sh if aim>amax: amax = aim amin = amax if aim<amin: amin = aim aim_k = amax/amin if aim_k>kmax: x_opt = [x, sh, w] kmax = aim_k print(' : {0}, : {1}'.format(x_opt[0], x_opt[1]))
图2标记了在找到的位移距离处设置的点。 如您所见,它们很好地标记了每个窗口。 即 我们已经知道地板的高度!
所考虑的算法可在各种住宅建筑物的外墙上找到良好的规则区域(图4)。

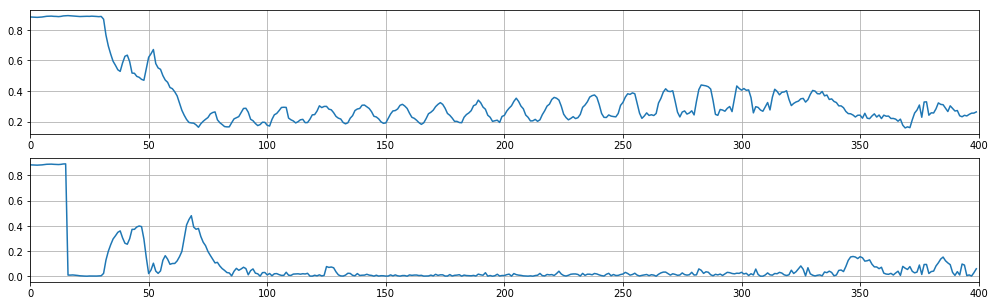

图4示例
步骤2.计算楼层数
在这一步,主要困难开始了。 进一步的操作可能如下:
- 通过分析平均亮度差异曲线或使用机器学习来估算房屋的高度)。 用房屋的高度除以地板的高度,得到楼层数。
- 在第一步中找到的窗口中,查找类似于窗口的对象并直接对它们进行计数,例如在特定点。
首先尝试第一种方法似乎很自然:一旦知道地板的高度,就可以确定房屋的高度。 但是,考虑到所有可能的边界和过渡,类似于步骤1中所示的方案证明非常不适合确定房屋的高度。 在某些情况下,可能会获得很好的工作实例,但是为了获得持续良好的结果,需要使用机器学习的方法。

图5使用随机森林确定房屋的高度