懒惰计算的概念几乎不值得详细讨论。 少做同一件事的想法已经久远,尤其是当它又长又沉时。 因为马上到了点。
根据本文的作者,普通的起偏镜应:
- 保存程序调用之间的计算。
- 跟踪计算树中的更改。
- 具有适度透明的语法。

概念图
为了:
- 保存程序调用之间的计算:
确实,如果我们每天调用同一个脚本数百次,那么如果有可能将结果对象存储在文件中,为什么每次调用该脚本时我们都要重新计算相同的脚本。 最好从磁盘中拉出一个对象,但是...我们必须确保它的相关性。 突然,脚本被重写,并且保存的对象已过期。 基于此,我们不能仅在文件存在时加载对象。 第二点由此得出。 - 跟踪计算树中的更改:
必须根据有关生成对象的函数的参数的数据来计算更新对象的需要。 因此,我们将确保加载的对象有效。 实际上,对于纯函数,返回值仅取决于参数。 这意味着,尽管我们缓存纯函数的结果并监视参数的变化,但我们可以对缓存的相关性保持冷静。 同时,如果计算的对象依赖于另一个缓存的(惰性)对象,而后者又依赖于另一个对象,则需要正确计算这些对象中的更改,并及时更新不再相关的链节点。 另一方面,考虑到我们并不总是需要加载整个计算链的数据,这将是一个很好的选择。 通常,仅加载最终结果对象就足够了。 - 具有适度透明的语法:
这一点很清楚。 如果为了将脚本重写为延迟计算而必须更改整个代码,则这是一般的解决方案。 应该进行最小程度的更改。
这一道理导致了一个技术解决方案,由evalcache库在python中进行了样式设置(本文结尾的链接)。
语法解决方案和工作机制
简单的例子import evalcache import hashlib import shelve lazy = evalcache.Lazy(cache = shelve.open(".cache"), algo = hashlib.sha256) @lazy def summ(a,b,c): return a + b + c @lazy def sqr(a): return a * a a = 1 b = sqr(2) c = lazy(3) lazyresult = summ(a, b, c) result = lazyresult.unlazy() print(lazyresult)
如何运作?
在这里引起您注意的第一件事是创建了惰性装饰器。 对于python python来说,这种语法解决方案是相当标准的。 惰性装饰器传递给一个缓存对象,在该对象中,lenificator将存储计算结果。 类似dict的接口的要求被叠加在缓存类型上。 换句话说,我们可以缓存实现与dict类型相同的接口的所有内容。 为了在上面的示例中进行演示,我们使用了Shelve库中的字典。
还向装饰器发送了一个哈希协议,他将使用该协议来构造对象的哈希键和一些其他选项(写许可权,读取许可权,调试输出),可以在文档或代码中找到它们。
装饰器可以应用于其他类型的函数和对象。 这时,一个惰性对象将基于它们的基础上构建,该哈希密钥是基于表示来计算的(或使用为此类型的函数专门定义的哈希函数)。
该库的一个关键功能是,一个懒惰的对象可以生成其他懒惰的对象,并且父对象(或多个父对象)的哈希将混合到后代的哈希键中。 对于惰性对象,允许使用获取属性的操作,对象的调用( __call__ )和运算符。
实际上,当通过脚本时,不执行任何计算。 对于b,不计算平方,对于lazyresult,不考虑参数的总和。 取而代之的是,构建操作树并计算惰性对象的哈希键。
实际计算(如果结果先前未放入高速缓存中)将仅在以下行中执行: result = lazyresult.unlazy()
如果对象是先前计算的,则将从文件中加载。
您可以可视化构建树:
构建树可视化 evalcache.print_tree(lazyresult) ... generic: <function summ at 0x7f1cfc0d5048> args: 1 generic: <function sqr at 0x7f1cf9af29d8> args: 2 ------- 3 -------
由于对象的哈希值是基于生成这些对象的参数的数据建立的,因此,当参数更改时,对象的哈希值也会随之更改,并且整个链的哈希值也将随之变化。 这使您可以通过及时更新来使高速缓存数据保持最新。
懒惰的对象在一棵树上排队。 如果我们对其中一个对象执行非常规操作,则将根据需要加载并计数尽可能多的对象以获得有效结果。 理想情况下,将简单地加载必要的对象。 在这种情况下,该算法不会将成型对象拉入内存。
在行动
上面是一个简单的示例,该示例显示了语法,但没有演示该方法的计算能力。
这是一个更接近现实生活的示例(供sympy使用)。
简化符号表达式的操作非常昂贵,字面上要求简化。 大型阵列的进一步构建需要更长的时间,但是由于简化,结果将从缓存中提取。 请注意,如果在生成sympy表达式的脚本顶部更改了任何系数,则由于惰性对象的哈希键将更改(由于使用了__repr__语句),因此将重新计算结果。
当研究人员对长时间生成的对象进行计算实验时,通常会发生这种情况。 它可以使用多个脚本来分离对象的生成和使用,这可能会导致数据更新不及时的问题。 所提出的方法可以促进这种情况。
这是怎么回事?
evalcache是zencad项目的一部分。 这是一个小脚本,启发并采用了与opencad相同的思想。 与面向网格的opencad不同,在opencascade核心上运行的zencad使用对象的brep表示,并且脚本以python编写。
几何运算通常执行很长时间。 cad脚本系统的缺点是,每次运行脚本时,都会完全重新计算产品。 此外,随着模型的增长和复杂化,间接费用成本不会线性增长。 这导致这样的事实,即您只能使用极小的模型舒适地工作。
evalcache的任务是解决此问题。 在zencad中,所有操作都被宣布为延迟。
范例:
模型构建示例
该脚本生成以下模型:
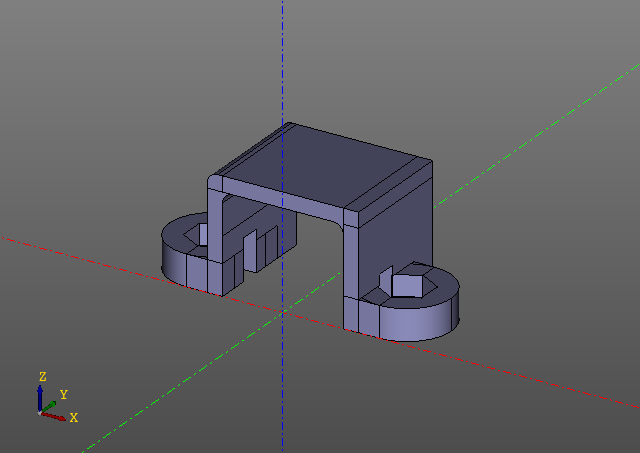
请注意,脚本中没有evalcache调用。 诀窍是,缩小率被嵌入到zencad库本身中,乍一看甚至看不到,尽管此处的所有工作都在处理惰性对象,并且仅在“显示”功能中执行直接计算。 当然,如果更改了某些模型参数,则会从第一个哈希键更改的地方重新计算模型。
庞大的计算模型这是另一个例子。 这次我们将仅限于图片:
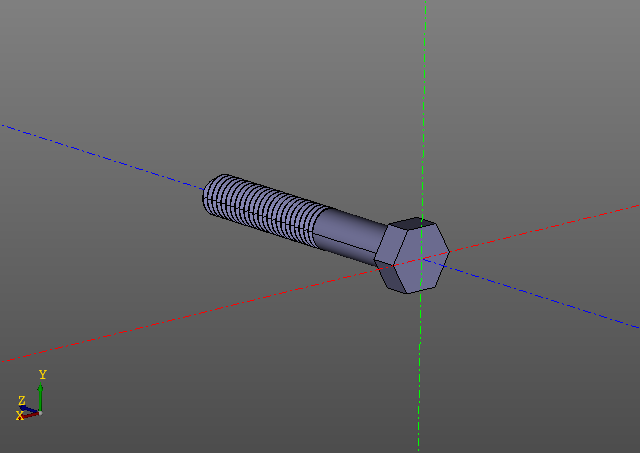
计算螺纹表面并非易事。 在我的计算机上,这样的螺栓建立在十秒的数量级上。使用缓存编辑带有线程的模型要轻松得多。
现在这是一个奇迹:

交叉螺纹表面是一项复杂的计算任务。 但是,实用价值无非是检查数学。 计算需要一分半钟。 值得奉献的目标。
问题所在
缓存可能无法正常工作。
缓存错误可分为误报和误报 。
错误的负错误
假否定错误是指计算结果在缓存中,但系统未找到它的情况。
如果evalcache由于某种原因使用的哈希密钥算法产生了不同的密钥进行重新计算,则会发生这种情况。 如果没有为哈希类型的对象重写哈希函数,则evalcache使用对象的__repr__构造键。
例如,如果要租用的类未覆盖标准object.__repr__ ,则该错误会发生错误,该object.__repr__都在变化。 或者,如果重写了__repr__ ,则在某种程度上取决于对变化数据(例如对象的地址或时间戳)的计算的__repr__ 。
不好:
class A: def __init__(self): self.i = 3 A_lazy = lazy(A) A_lazy().unlazy()
好:
class A: def __init__(self): self.i = 3 def __repr__(self): return "A({})".format(self.i) A_lazy = lazy(A) A_lazy().unlazy()
错误的负错误会导致事实证明,放大率无效。 该对象将在每次执行新脚本时重新计数。
误报错误
这是一种错误类型的错误,因为它会导致最终计算对象出现错误:
发生这种情况有两个原因。
- 难以置信:
哈希键冲突发生在缓存中。 对于空间为115792089237316195195423570985008687907853853984984665640564039457584007913129639936可能的键的sha256算法,可以忽略碰撞的可能性。 - 可能:
对象的表示形式(或覆盖的哈希函数)不能完全描述它,或者与另一种类型的对象的表示形式一致。
class A: def __init__(self): self.i = 3 def __repr__(self): return "({})".format(self.i) class B: def __init__(self): self.i = 3 def __repr__(self): return "({})".format(self.i) A_lazy = lazy(A) B_lazy = lazy(B) a = A_lazy().unlazy() b = B_lazy().unlazy()
这两个问题都与不兼容的__repr__对象有关。 如果由于某种原因无法覆盖__repr__对象类型,则该库允许您为用户类型设置特殊的哈希函数。
关于类似物
有许多简化库基本上认为每个脚本调用最多运行一次计算就足够了。
根据您的要求,有许多磁盘缓存库将为您保存带有必需密钥的对象。
但是我仍然找不到允许在执行树上缓存结果的库。 如果有,请不安全。
参考文献:
Github项目
Pypi项目