最快的狂野西部浮点数

在实现一个“阅读器”的过程中，随着计算精度的提高出现了一个问题。 该计算算法可以在标准浮点数上快速运行，但是当连接了用于精确计算的库时，一切开始急剧减速。 在本文中，我们将考虑使用多分量方法扩展浮点数的算法，由于浮点算法是在cp芯片上实现的，因此有可能实现加速。 这种方法对于更精确地计算数值导数，矩阵求逆，多边形修整或其他几何问题很有用。 因此，可以在不支持它们的视频卡上模拟64位浮点数。

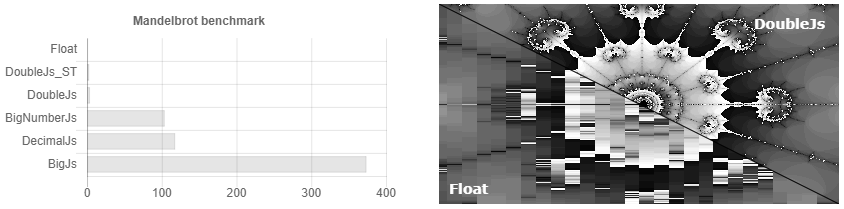
引言

由于Nikluas Wirth遗赠给我们以保持数字0和1，因此我们将它们存储在其中。 难道人类生活在十进制中，看似普通的数字0.1和0.3在二进制系统中不能用有限的分数表示吗？ 对它们进行计算时，会遇到文化冲击。 当然， 正在尝试为基于十进制的处理器创建库， IEEE甚至采用了标准化格式。

但是现在，我们在所有地方都考虑了二进制存储，并使用库进行所有金钱计算以进行精确计算，例如bignumber，这会导致性能损失。 营销人员说，Asik会考虑使用加密，而在处理器中，这种十进制算术运算空间很小。 因此，当数字以未变换的数字总和的形式存储时，多分量方法是一种方便的技巧，并且在理论信息学领域是一个积极发展的领域。 尽管Decker仍然学会了正确地进行乘法运算而又不失准确性，但在1971年，现成的库（MPFR，QD）出现的时间要晚得多，并且不是所有语言都出现了，显然是因为并非所有的IEEE标准都支持它，但是更严格的证明了计算错误，例如在2017年推出双字运算。

双字算术

有什么意义？ 在有胡子的时期，没有浮点数的标准，为了避免舍入的问题，Møller提出了建议，而Knuth后来证明了无差值求和。 以这种方式运行

function quickTwoSum(a, b) { let s = a + b; let z = s - a; let e = b - z; return [s, e]; } 

在此算法中，假设 $$$| a | > | b |$，则它们的确切总和可以表示为两个数字的总和 $$$s + e$您可以成对存储它们以进行后续计算，并且减法被减为负数。



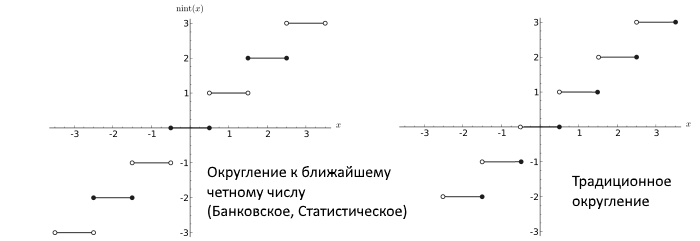
后来，Dekker表明，如果使用的浮点数舍入到最接近的偶数（四舍五入到偶数，这通常是正确的过程，在长时间的计算和IEEE标准中不会导致大的误差），然后有一个无错误的乘法算法。

 function twoMult(a, b) { let A = split(a); let B = split(b); let r1 = a * b; let t1 = -r1 + A[0] * B[0]; let t2 = t1 + A[0] * B[1]; let t3 = t2 + A[1] * B[0]; return [r1, t3 + A[1] * B[1]]; } 

其中split（）是Weltkamp先生分割数字的算法

 let splitter = Math.pow(2, 27) + 1; function split(a) { let t = splitter * a; let d = a - t; let xh = t + d; let xl = a - xh; return [xh, xl]; } 

使用常量 $$$C = 2 ^ s + 1$它等于尾数长度的一半多一点，这不会在乘法过程中导致数字溢出，而是将尾数分为两半。 例如，对于64位的字长，尾数的长度为53，则s = 27。



这样，Dekker提供了双字算术计算所需的几乎完整的集合。 从那里开始，还指出了如何对两个双字数字进行乘，除和平方运算。

他的用于对两个双字求和的quickTwoSum算法到处都是“内联”，并且使用了校验 $$$| a | > | b |$。 如[4]中所述，在现代处理器上，使用带数字的附加操作比分支算法便宜。 因此，以下算法现在更适合于将两个单字数字相加

 function twoSum(a, b) { let s = a + b; let a1 = s - b; let b1 = s - a1; let da = a - a1; let db = b - b1; return [s, da + db]; } 

这就是双字数字的总和与乘法。

 function add22(X, Y) { let S = twoSum(X[0], Y[0]); let E = twoSum(X[1], Y[1]); let c = S[1] + E[0]; let V = quickTwoSum(S[0], c); let w = V[1] + E[1]; return quickTwoSum(V[0], w); } function mul22(X, Y) { let S = twoMult(X[0], Y[0]); S[1] += X[0] * Y[1] + X[1] * Y[0]; return quickTwoSum(S[0], S[1]); } 

一般来说，有关双字算术，理论错误边界和实际实现的算法的最完整，最准确的列表在2017年的链接[3]中进行了描述。 因此，如果有兴趣，我强烈建议您直接去那里。 通常，在[6]中给出了四字算法，在[5]中给出了任意长度的多分量扩展算法。 仅在那里，在每次操作之后，都使用了重归一化过程，这对于小尺寸而言并不总是最佳的，并且没有严格定义QD中的计算精度。 通常，值得考虑的是这些方法的适用性限制。

恐怖故事javascript-a。 decimal.js与bignumber.js与big.js的比较。

碰巧，几乎所有用于js中精确计算的库都是由一个人编写的。 尽管他们几乎都是一样的，但是却产生了选择的幻觉。 此外，文档没有明确指出如果您在每次乘法/除法运算后不对数字进行四舍五入，那么数字的大小将一直加倍，并且算法的复杂性在x3500中会变得很容易。 例如，如果没有四舍五入，则它们的计算时间比较可能看起来像这样。



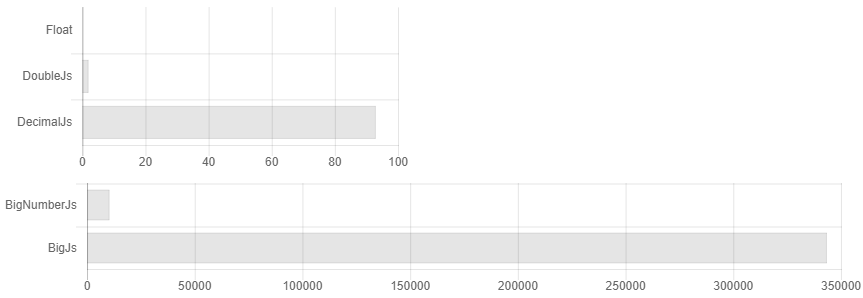
也就是说，您将精度设置为32位小数，然后...糟糕，您已经有64位数字，128位。我们认为非常准确！ 256，512 ...但是我设置了32！.. 1024，2048 ...这样的开销出现了3500次。 该文档指出，如果您具有科学的计算能力，那么decimal.js可能更适合您。 尽管实际上，如果您只是定期取舍，那么对于科学计算，Bignumber.js的运行速度要快一些（见图1）。 如果不能找零，谁需要计算一分钱的百分之一呢？ 在任何情况下，当我需要存储更多指示的数字并且无法再输入一些额外的字符时，该怎么办？ 当没人知道泰勒级数对任意数的收敛的严格精度时，如何得出这样一个庞然大数的正弦？ 通常，没有毫无根据的怀疑，例如可以使用Schoenhage-Strassen乘法算法并使用Cordic计算来找到正弦值，从而提高计算速度。

Double.js

我想说，当然，Double.js可以快速准确地计数。 但这并非完全正确，也就是说，它认为的速度要快10倍，但并不总是准确的。 例如，它可以处理0.3-0.1，并转为双重存储，反之亦然。 但是Pi编号可以将近32位数字的双精度进行解析，并且无法解决。 16号产生一个错误，好像正在发生溢出一样。 总的来说，由于我被困住了，我敦促js社区一起努力解决解析问题。 我尝试以数字方式解析并以双精度除法，如在QD中一样，以16位数字为单位分割并以双精度除法，使用Julia.lib之一中的Big.js分割尾数。 现在，我犯了一个.parseFloat（）错误，因为即使使用ECMAScript 1，也支持四舍五入到最接近整数的IEEE标准。尽管您当然可以尝试绑定二进制缓冲区并观察每个0和1。通常，如果可以解决此问题，则然后，可以使用bignumber.js中的x10-x20加速度以任意精度进行计算。 但是，许多Mandelbrot已经可以渲染质量，您可以将其用于几何任务。

一年后，我回到这里，仍然解决了解析问题。 问题仅在于准确度不足（乘以10 ^（-n））。 所有算法都从头进行了修改，现在以惊人的准确性和速度运行。



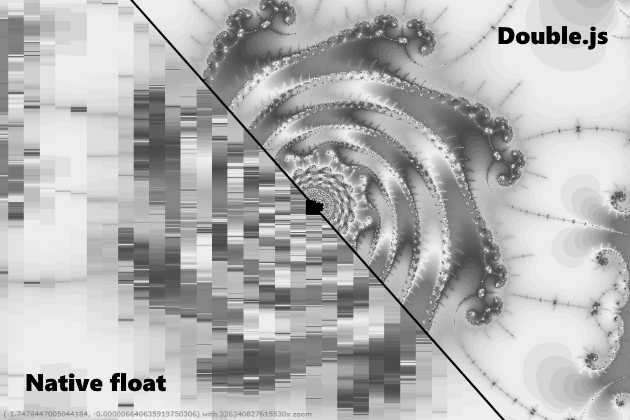
这是lib的链接，有一个交互式基准测试和一个沙箱，您可以在其中使用它。

使用的来源

1. O.Møller。 浮点运算中的拟双精度。 ，1965年。
2. 西奥多罗斯·德克（Theodorus Dekker）。 一种用于扩展可用精度的浮点技术 ，1971年。[ 查看器 ]
3. Mioara Joldes，Jean-Michel Muller和Valentina Popescu。 双字运算的基本构建块的严格严谨的误差范围 ，2017年。[ PDF ]
4. 穆勒，J.-M。 Brisebarre，N。de Dinechin等 浮点算法手册，第14章，2010年。
5. 乔纳森·舒丘克（Jonathan Shewchuk）。 鲁棒的自适应浮点几何谓词 ，1964年。[ PDF ]
6. 飞ida阳三，李小野，大卫·贝利。 Double-Double和Quad-Double算法的库 ，2000年。[ PDF ]